[알고리즘] 누적합(prefix sum)

누적합 알고리즘은 배열이나 리스트와 같은 데이터 구조에서 각 요소까지의 합을 계산하는 알고리즘이다. 이 알고리즘은 특정 요소의 값을 구할 때 매번 모든 요소를 다시 계산하는 것이 아니라 이전까지의 합을 이용하여 효율적으로 계산한다.

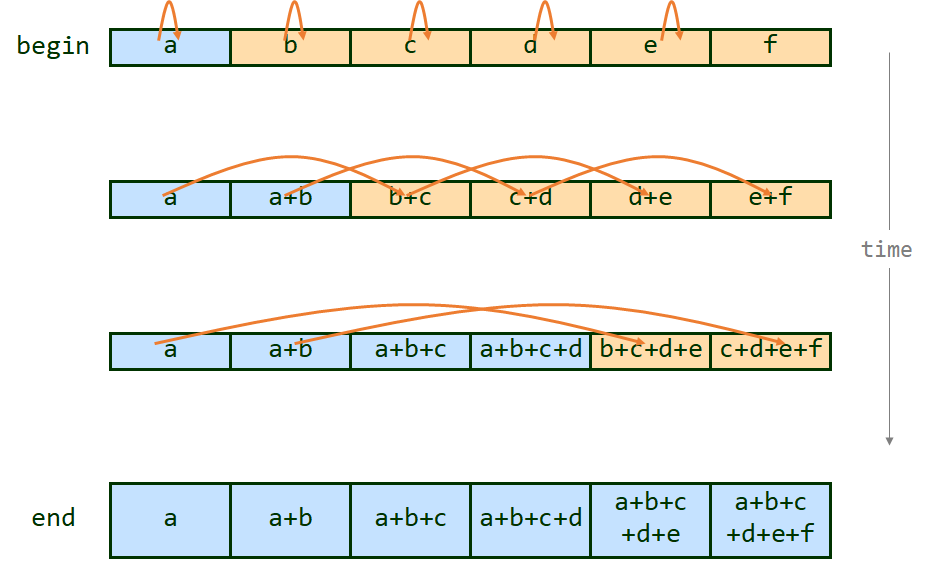
간단한 예제로 [1, 2, 3, 4, 5] 라는 배열이 주어졌다고 해보자.

1. 초기 누적합 변수를 설정한다. 여기서는 0으로 설정한다.
2. 배열의 첫 번째 요소부터 시작하여 각 요소를 현재 누적합에 더한다.
3. 현재 누적합을 해당 요소의 누적합으로 저장한다.
4. 배열의 끝까지 이 과정을 반복한다.

• 요소 1: 누적합 = 0 + 1 = 1
• 요소 2: 누적합 = 1 + 2 = 3
• 요소 3: 누적합 = 3 + 3 = 6
• 요소 4: 누적합 = 6 + 4 = 10
• 요소 5: 누적합 = 10 + 5 = 15

따라서 최종적으로 배열 [1, 2, 3, 4, 5]의 각 요소까지의 누적합은 [1, 3, 6, 10, 15]가 된다.

시간 복잡도, 공간 복잡도

누적합 알고리즘의 시간 복잡도는 입력 배열의 크기에 선형적으로 비례한다. 즉, 배열의 크기가 N일 때, 시작 복잡도는 O(N)이다. 이는 배열의 각 요소를 한번씩만 방문하여 누적합을 계산하기 때문에 발생한다. 시간 복잡도가 선형이므로 입력 배열의 크기에 비례하여 알고리즘 실행 시간이 증가한다.

공간 복잡도는 추가적인 배열을 사용하여 누적합을 저장하는 데 필요한 공간을 나타낸다. 입력 배열의 크기가 N일 때, 추가적인 배열의 크기도 N이 된다. 따라서 누적합 알고리즘의 공간 복잡도 역시 O(N)이다. 이는 입력 배열과 같은 크기의 배열을 추가로 사용하기 때문에 발생한다.

이미지 출처