이 게시글은 장형기님의 SLAM 기술면접 질문 100선에 대한 제 나름대로의 답을 정리한 것입니다.
KD-Tree(K-dimensional Tree):
Binary Search Tree를 확장한 개념으로, k차원 공간의 점들을 구조화하는 공간 분할 자료 구조
Binary Search Tree란?
데이터를 저장할 때 크기가 큰지 작은지만 비교하여 저장 공간을 정하는 방식
데이터가 들어오게 되면 부모 노드와 비교하여 작으면 왼쪽 잎새 노드에 저장하고 크면 오른쪽 잎새 노드에 저장합니다.
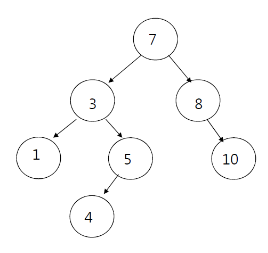
그림을 살펴 보면 7을 기준으로 작은 값인 3은 왼쪽에 저장되고 큰 값인 8은 오른쪽에 저장됩니다.
그 후 들어오는 데이터는 이 기준에 따라 비교되어 내려오다 자신에게 맞는 위치의 잎새 노드에 저장됩니다.
이러한 기준으로 정렬했기 때문에 데이터를 찾을 때 탐색해야할 위치를 쉽게 찾을 수 있는 장점이 있지만 데이터가 순서대로 들어온다면 계산 복잡도가 늘어나는 단점도 있습니다.
이제 이를 확장한 kd-tree에 대해 알아봅시다.
kd-tree는 하나의 값의 크기를 비교하는 binary search tree를 확장하여 높은 차원의 vector도 저장할 수 있습니다.
kd-tree에서의 분할 기준은 binary search tree와 같이 값의 크기입니다.
차원이 큰 vector에는 많은 값이 들어있는데 어떤 값을 비교해야할까요?
data 차원 중 가장 분산값이 큰 차원의 값들을 비교하여 data를 정렬하게 됩니다.
예를 들어보겠습니다.
X={x1:(3,1),x2:(2,3),x3:(6,2),x4:(4,4),x5:(3,6),x6:(8,5),x7:(7,6.5),x8(5,8),x9:(6,10),x10:(6,11)}
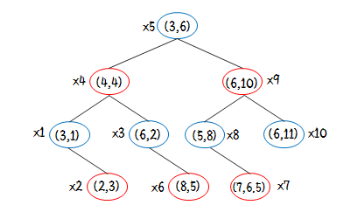
이것은 데이터 x를 kd-tree로 정렬한 것입니다. 이것을 어떻게 배열하였는지 함께 살펴보겠습니다.
이 벡터들의 첫번째 차원의 분산은 3.4이고 두번째 차원의 분산은 9.9025이므로 2번째 차원 값을 기준으로 첫 tree를 만들게 됩니다.
x5(3,6)를 기준으로 두개로 분할하게되면
X_left = {x1(3,1),x3(6,2),x2(2,3),x4(4,4),x6(8,5)}
x_right = {x7(7,6.5),x8(5,8),x9(6,10),x10(6,11)}
두가지로 나눌 수 있고 이를 반복하여 시행하면 kd-tree가 완성됩니다.
이해를 돕기 위해 x_left를 한번 더 분할한다면
분산이 큰 첫번째 차원으로 분할되고 x4를 중간값으로 둔 후
x_left2 = {x2(2,3),x1(3,1)}
x_right2 = {x3(6,2),x6(8,5)} 로 다시 분할할 수 있습니다.
LiDAR Processing에서 K-D tree를 어떤 방법으로 이용할 수 있을까요?
보통 Point Cloud를 탐색할 때 많이 사용됩니다.
nearestKSearch나 radiusSearch를 할 때 K-D tree로 정리된 Point Cloud를 활용합니다.
빠른 시간안에 Point Cloud를 찾을 수 있기 때문에 많이 활용하고 있습니다.
이를 통해 Point들을 Clustering하거나 registration을 진행하기도 하고 Outlier를 제거하기도 합니다.
옛날에 K-D tree를 정리해둔게 있어서 그것 바탕으로 새로 작성해서 편했네요.
감사합니다.
