Robust kernel (또는 M-estimator)에 대해 설명해주세요.

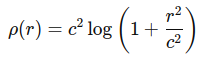
이 게시글은 장형기님의 SLAM 기술 면접 질문 100선을 정리한 것입니다.

---

우리는 optimization을 할 때 처음으로 배우는 것이 mean square error를 최소화하는 식입니다.
이러한 방법에는 크게 두 가지 단점이 존재합니다.

1. Outilier에 굉장히 취약하다

2. Edge로 만드는 constraints가 Gaussian distribution을 따른다고 가정한다

실제 data가 gaussian distribution을 따르지 않는다면 문제가 발생하게 됩니다.

Robust Kernel은 outlier나 noise의 영향을 줄이기 위해 설계된 optimization 함수를 말합니다.

---

주요 Robust Kernel 함수

1. Huber Kernel

• 정의: 작은 residual에 대해서는 $L_2$ loss를 사용하고, 큰 residual에서는 $L_1$ loss로 전환됩니다.

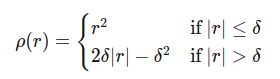
• 특징: $L_2$와 $L_1$의 장점을 결합하여 outlier의 영향을 덜 받습니다.

2. Cauchy Kernel

• 정의: residual이 커질수록 loss의 증가율을 억제

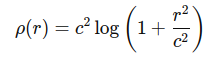
• 특징: residual이 클수록 loss function이 천천히 증가

3. Tukey Kernel

• 정의: 일정 크기 이상의 residual에 대해 loss를 상수로 유지

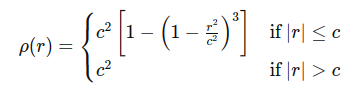
• 특징: 극단적 outlier를 완전히 무시

---

M-Estimator

이러한 커넬의 모양을 따라, residual r 값에 따른 weight를 새로 지정하는 방법이 M-Estimator입니다.

수식: $min_M\Sigma_{d\in D}r(d|M)^2$

kernel함수를 이용하여 estimation을 하는 방법이라고 생각하시면 되겠습니다.

---

장단점

• 장점

1. Outlier 처리: outlier로 인해 모델이 왜곡되는 것을 막아줍니다.

2. 일반화 성능 향상: 모델이 전체 데이터 분포를 더 잘 반영하게 해줍니다.

3. 효율성: 데이터를 손상시키는 요소를 효과적으로 억제해줍니다.

• 단점

1. hyperparameter 사용: hyperparameter를 사용하기 때문에 설정값에 따라 성능이 차이가 날 수 있습니다.

2. 복잡성 증가: 단순 loss 함수보다 수식이 더 복잡해지고 계산 비용이 증가합니다.

3. 기존 데이터와의 충돌 가능성: 데이터에 이상치가 적거나 없는 경우, 불필요한 억제를 가하면서 성능이 떨어질 수도 있습니다.

---

Kernel 함수를 통해 이상치에 더 강건하게 optimization을 할 수 있다는 것이 중요한 점 같습니다.