[코테]04-건너 뛰며 해보기

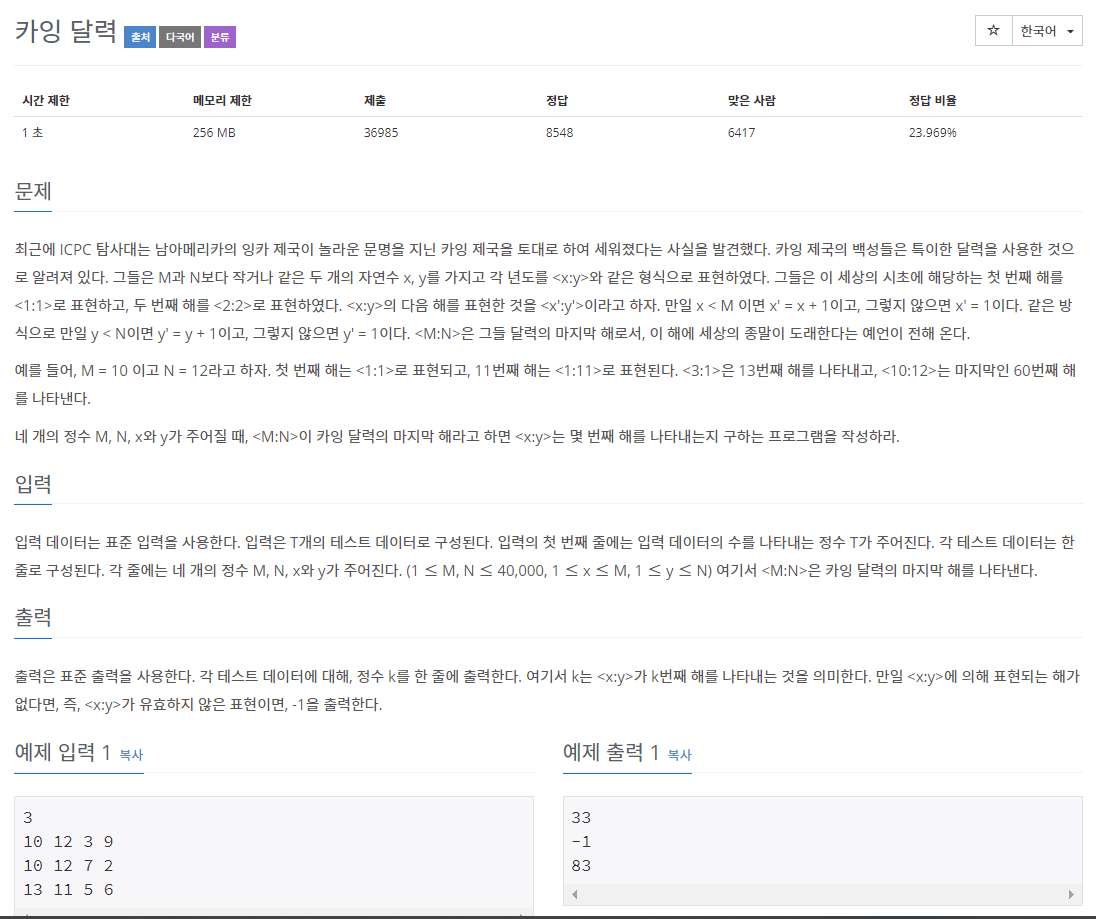
카잉 달력

M과 N보다 작거나 같은 두 자연수 x,y를 이용해서 년도를 <x:y>로 표현한다.
첫 번째 해는 <1:1>, 두 번째 해는 <2:2>이다
<x:y>의 다음 해는 <x':y'>이다.
- x < M 이면 x'=x+1, 아니면 x'=1
- y < N 이면 y'=y+1, 아니면 y'=1
M,N,x,y가 주어졌을 때, <x:y>이 몇 번째 해인지 구하는 문제
1 <= M,N <= 40,000
전체 경우의 수는 MN=1,600,000,000가지라서 너무 많다.

• 모든 경우의 수를 다 적용해보기에는 경우의 수가 너무 많기 때문에 다른 방법으로 풀어야함.
• E S M 날짜 계산이랑 비슷한 문제임.
• x는 M으로 나눈 나머지, y는 N으로 나눈 나머지.
• x,y가 주어지기 때문에 모든 해를 고려하는 것이 아니라 i*M +x의 형태만 조사
• 시간복잡도는 O(N)이 된다.

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		
		Scanner sc = new Scanner(System.in);
		int num = sc.nextInt();
		
		for(int j=0;j<num;j++) {
			int res=0;
			int m = sc.nextInt();
			int n = sc.nextInt();
			int x = sc.nextInt();
			int y = sc.nextInt();
			
			int max = m*n;
			int i = 0;
			
			if(y==n)
				y=0;
			
			while(true) {
				if((m*i+x) % n ==y) {
					res = m*i + x;
					break;
				}
				if(m*i + x > max) {
					res = -1;
					break;
				}
				i++;
			}
			System.out.println(res);
		}

	}
}

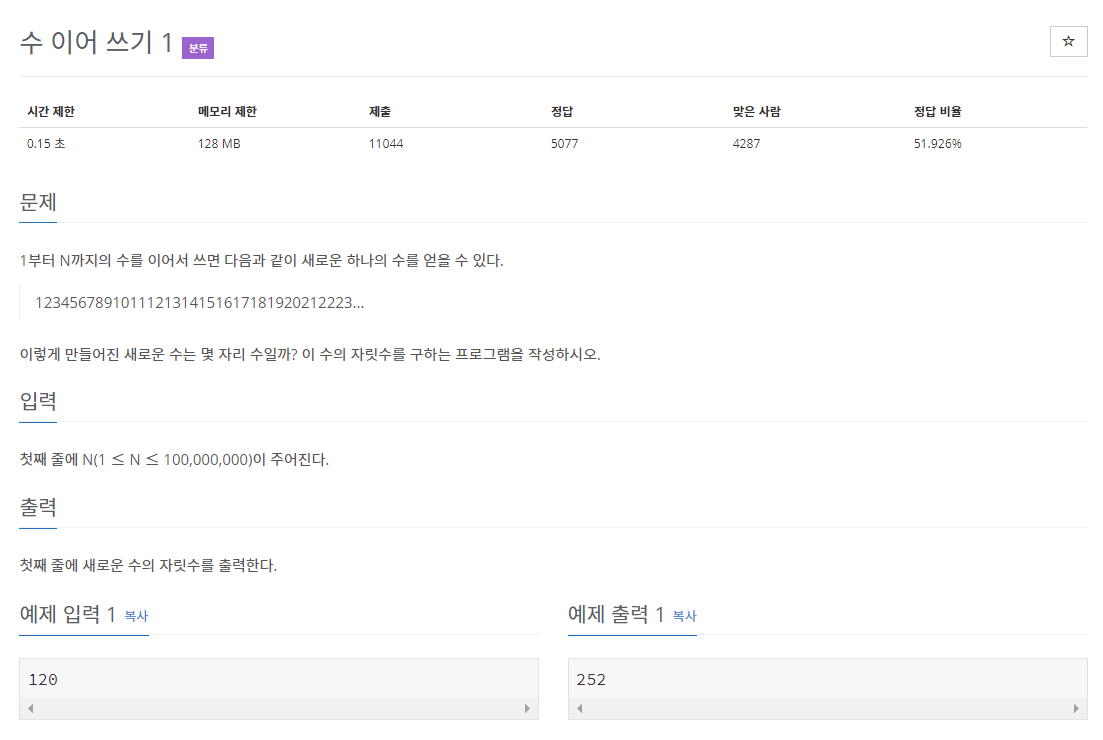
수 이어 쓰기1

1부터 N까지 수를 이어서 쓰면 새로운 하나의 수를 얻게된다.(1<=N<=100,000,000)
이 때 새로운 수는 몇자리 일까?

• 중복되는 계산이 많은 것을 이용해서 한 번에 처리.
• N이 너무 크기 때문에, 실제로 수를 만드는 것은 시간 너무 오래걸림.
• 시간복잡도 O(N)이여도 1억이기 때문에..
• 1부터 9까지는 길이가 1씩 증가,
• 10부터 99까지는 길이가 2씩 증가,
• 100부터 999까지는 길이가 3씩 증가,
• 1000부터 9999까지는 길이가 4씩 증가,
• 자리 수의 개수를 구해서 다 더해줌 (9-1+1)1 + (99-10+1)2 + ...
• N이 9자리이기 때문에 9번만 계산해주면 됨.

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		
		Scanner sc = new Scanner(System.in);
		int num = sc.nextInt();
		long res =0;
		
		for(int i=1;i<=num;i*=10) {
			res += num- (i-1);
		}
		System.out.println(res);
	}
}

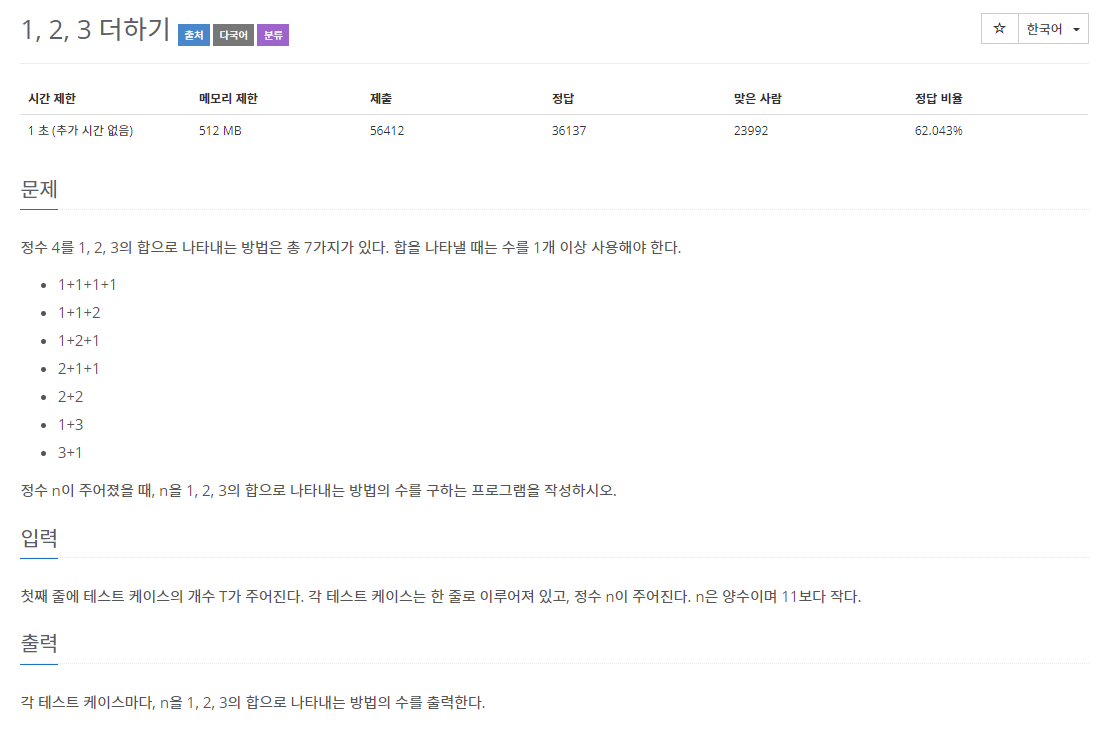
1,2,3 더하기

정수 n을 1,2,3의 합으로 나타내는 방법의 수를 구하는 문제
n = 4
1+1+1+1
1+1+2
1+2+1
2+1+1
2+2
1+3
3+1

• 재귀함수를 써서 할 수도 있고 n중 포문 가능하긴한데 그렇게 쓰진않음.
• 똑같은 부분이 반복될 때는 재귀함수를 사용하면 됨.
  

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		
		Scanner sc = new Scanner(System.in);
		int num = sc.nextInt();
		int arr[] = new int[11];
		arr[1]=1; 
		arr[2]=2;
		arr[3]=4;
		//1,2,3을 넣었을 때의 경우의 수를 지정.
		
		for(int i=0;i<num;i++) {
			int a = sc.nextInt();
			
			for(int j=4;j<=a;j++) {
				arr[j]= arr[j-1] + arr[j-2] + arr[j-3];
			}
			System.out.println(arr[a]);
		}
		
	}
}

=> 재귀함수를 쓰지 않고 어차피 1,2,3만 더하는 것을 이용해서 풀었다. 1을 넣었을 때 경우의 수 1, 2를 넣었을 때 2, 3을 넣었을 때 4개를 배열에 넣어놓고 이중 포문을 사용했다.