
백트래킹
- 재귀 함수를 이용해 브루트포스를 하다 보면 더이상 호출이 의미 없음.
- 이 때, 이런 경우를 제외하고 브루트 포스를 진행하면 백트래킹이라고 함.
스타트와 링크
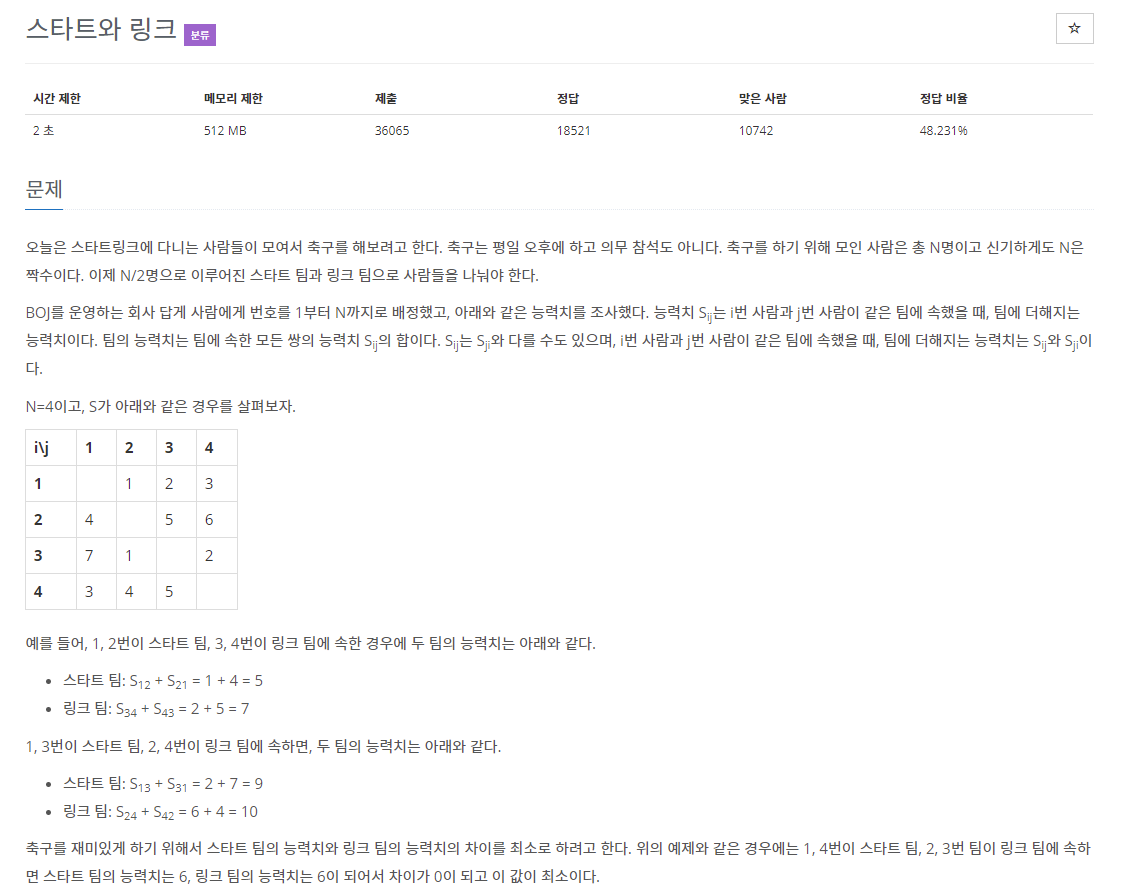
N명을 N/2명씩 두 팀으로 나누려고 한다. (4<=N<=20,N은 짝수)
두 팀의 능력치를 구한 다음, 차이의 최소값을 구하는 문제
S[i][j]=i번 사람과 j번 사람이 같은 팀에 속했을 때, 팀에 더해지는 능력치
팀의 능력치 : 팀에 속한 모든 쌍의 S[i][j]의 합
- 2^n가지의 경우의 수
- 사람을 어떤 팀에 넣을지 결정
- go(index,first,second)
index번째 사람을 어떤 팀에 넣을지 결정해야함
1번 팀과 2번 팀에 속한 사람이 각각 first, second에 들어가 있음. - 정답을 찾은 경우
index==n - 다음 경우
1번팀 : go(index,first,second)
2번팀 : go(index,first,second)
두 경우 모두 호출 전에 first또는 second에 index를 넣고 호출 후에 빼는 과정 필요
import java.util.*;
public class Main {
static int s[][];
static int n;
static int go(int index,ArrayList<Integer> first,ArrayList<Integer> second) {
if(index==n) { //정답 찾은 경우
if(first.size()!=n/2)
return -1;
if(second.size()!=n/2)
return -1;
//각 사이즈가 n/2가 아니라면 바로 반환
int t1=0;
int t2=0;
for(int i=0; i<n/2;i++) {
for(int j=0;j<n/2;j++) {
if(i==j) continue;
t1 += s[first.get(i)][first.get(j)];
t2 += s[second.get(i)][second.get(j)];
}
}
int diff= t1-t2;
if(diff<0)
diff = -diff;
return diff;
}
int min=-1;
if(first.size()>n/2)
return -1;
if(second.size()>n/2)
return -1;
//각 사이즈가 n/2보다 커졌을때 바로 반환.
first.add(index);
int t1 = go(index+1,first,second);
if(min == -1 || ( t1 != -1 && min > t1)) {
min = t1;
}
first.remove(first.size()-1);
second.add(index);
int t2= go(index+1, first,second);
if(min == -1 || (t2 != -1 && min > t2)) {
min = t2;
}
second.remove(second.size()-1);
return min;
}
public static void main(String[] args) {
Scanner sc= new Scanner(System.in);
n= sc.nextInt();
s= new int[n][n];
for(int i=0;i<n;i++) {
for(int j=0;j<n;j++) {
s[i][j]=sc.nextInt();
}
}
ArrayList<Integer> first = new ArrayList<Integer>();
ArrayList<Integer> second = new ArrayList<Integer>();
System.out.println(go(0, first, second));
}}링크와 스타트
import java.util.*;
public class Main {
static int s[][];
static int n;
static int go(int index,ArrayList<Integer> first,ArrayList<Integer> second) {
if(index==n) {
if(first.size()==0)
return -1;
if(second.size()==0)
return -1;
int t1=0;
int t2=0;
for(int i=0; i<first.size();i++) {
for(int j=0;j<first.size();j++) {
if(i==j) continue;
t1 += s[first.get(i)][first.get(j)];
}
}
for(int i=0; i<second.size();i++) {
for(int j=0;j<second.size();j++) {
if(i==j) continue;
t2 += s[second.get(i)][second.get(j)];
}
}
int diff= t1-t2;
if(diff<0)
diff = -diff;
return diff;
}
int min=-1;
first.add(index);
int t1 = go(index+1,first,second);
if(min == -1 || ( t1 != -1 && min > t1)) {
min = t1;
}
first.remove(first.size()-1);
second.add(index);
int t2= go(index+1, first,second);
if(min == -1 || (t2 != -1 && min > t2)) {
min = t2;
}
second.remove(second.size()-1);
return min;
}
public static void main(String[] args) {
Scanner sc= new Scanner(System.in);
n= sc.nextInt();
s= new int[n][n];
for(int i=0;i<n;i++) {
for(int j=0;j<n;j++) {
s[i][j]=sc.nextInt();
}
}
ArrayList<Integer> first = new ArrayList<Integer>();
ArrayList<Integer> second = new ArrayList<Integer>();
System.out.println(go(0, first, second));
}
}
부등호
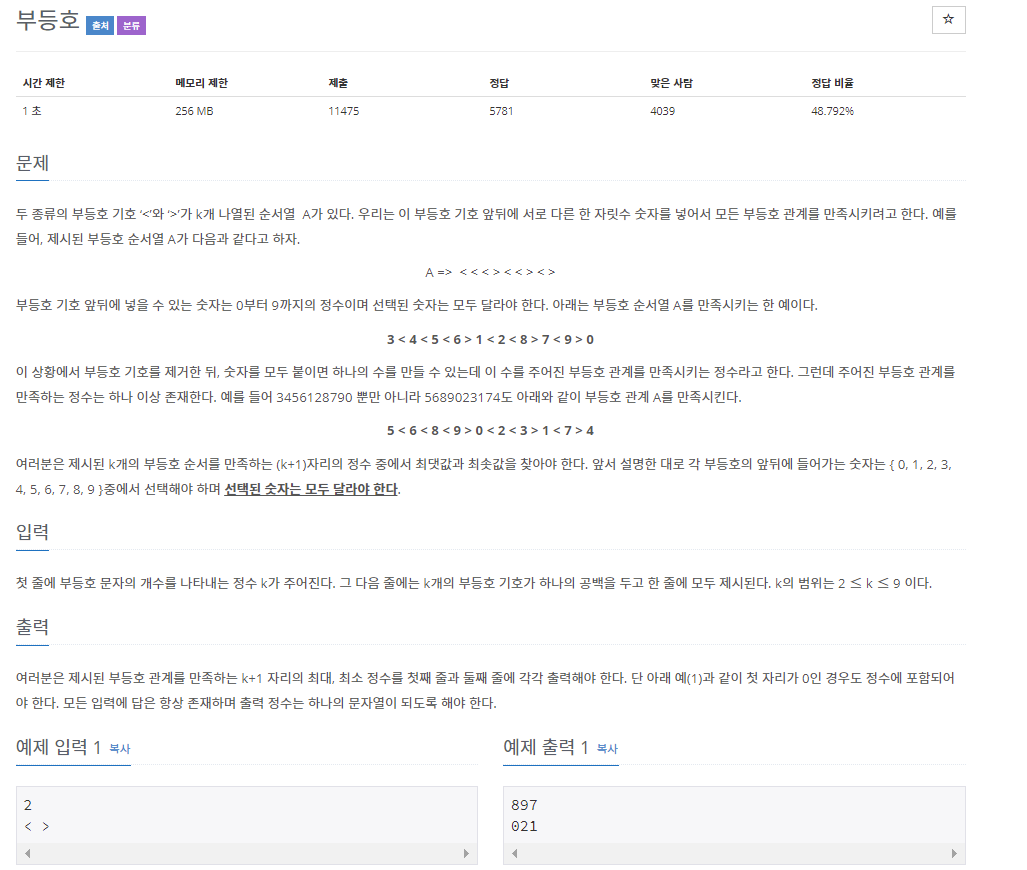
부등호 기호 <와 >가 나열된 수열 A가 있다.
기호의 앞,뒤에 한 자리 숫자를 넣어서 모든 부등호 관계를 만족시키려고 한다.
이 때, 선택된 수는 모두 달라야 한다.
k개의 부등호 관계를 모두 만족시키는 (k+1)개 자리의 정수 중에서 최대값과 최소값을 구하는 문제
-
기준이 되는 것은 위치.
-
< > < < _
-
이런식으로 되어있으면 각 index와 위치가 중요함.
-
부등호가 k개 있음.
-
수는 k+1개를 넣어야함.
-
i 번째수와 i+1번째수는 i번째의 부등호로 비교해야함.
-
첫번째 수에 6을 넣고 두번째 수에 5를 넣었을때 중간에 부등호가 < 라면,
그 이후에는 어떤 수가 들어가는지 의미가 없음.
-> 만약 이런 경우가 존재하면 함수 호출을 하지 않음. -
사용하지 않았으면, 그리고 대소관계를 지킬때만 함수 호출을 하면 시간을 크게 줄일 수 있음.
-
good이라는 함수는 두 숫자 x,y가 부등호 op의 관계인지를 확인해줌.
import java.util.*;
public class Main {
static boolean check[] = new boolean[10];
static int n;
static char a[] = new char[10]; //부등호
static ArrayList<String> res = new ArrayList<String>();
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n=sc.nextInt();
for(int i=0;i<n;i++) {
a[i]=sc.next().toCharArray()[0];
}
go(0,"");
Collections.sort(res);
System.out.println(res.get(res.size()-1));
System.out.println(res.get(0));
}
//부등호 맞는지 검사하는 함수 ok
static boolean ok(char a,char b,char c) {
if(c=='<') {
if(a>b) {
return false;
}
}
if(c=='>') {
if(a<b) {
return false;
}
}
return true;
}
static void go(int index, String num) {
if(index == n+1) {
res.add(num);
return;
}
for(int i=0;i<10;i++) {
if(check[i]) //사용하지 않았는지 비교
continue;
if(index==0 || ok(num.charAt(index-1),(char)(i+'0'),a[index-1])) {
//index가 0일 때는 비교가 안되니까 그 이후에 부등호 대소문자 맞는지 확인 후 검사하고 재귀함수 호출
check[i]=true;
go(index+1,num+Integer.toString(i));
check[i]=false;
}
}
}
}
맞춰봐
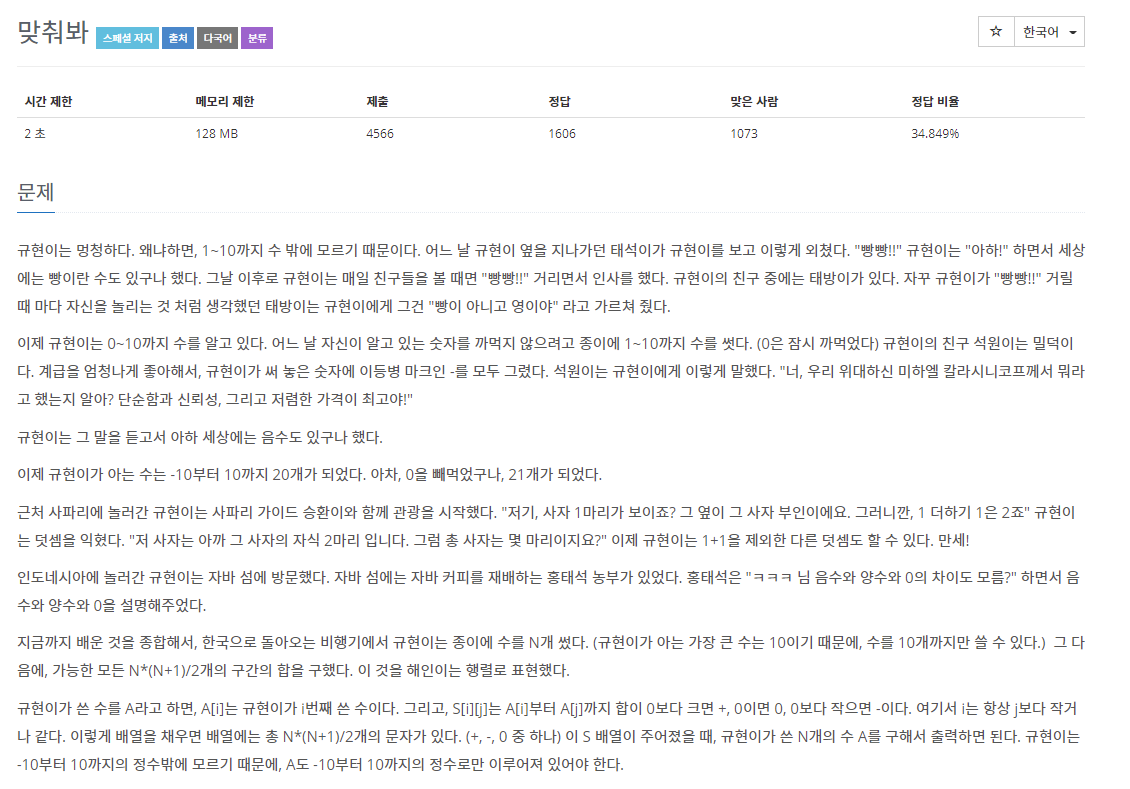
~~문제가 왜케 길어..? ~~
-10부터 10까지 N개의 정수로 이루어진 수열 A가 있다. (N<=10)
S[i][j]=A[i]+A[i+1]+...+A[j]가 0보다 크면 +, 작으면 -, 같으면 0
S가 주어졌을 때, 가능한 A를 아무거나 찾는 문제
-
수의 위치가 중요함. => 문제의 기준 : 위치
-
-10~10 / -10~10 / .... (중복 상관없기 때문에)
-
전체 경우의 수는 21^10 , 경우의 수가 너무 많음.
-
N과 M(3)과 똑같은 문제.
-
하지만 경우의 수가 너무 많기 때문에 경우의 수를 줄일 방법을 찾아야 함.
-
S배열에서 중요한 부분은 i==j일 때,
S[i][j]=A[i]의 부호와 같기 때문임. 이런 조건을 추가해주면 경우의 수가 줄어듬
-
그래도 경우의 수가 10^10이라서 시간 초과가 나게 됨.
다른 조건을 추가해줘야함. -
어떤 i번째의 수를 정하면 S[j][i]의 부호를 검사할 수 있음.
-
index번째 수를 결정하면, 0~index번째 수는 변하지 않음.
따라서, 모든 sign[k][index] (0<=k<index)를 go(index)에서 검사할 수 있음. -
check(index)함수의 역할 : index번 째의 수를 결정했다고 가정해야함.
결정해야 부호를 비교할 수 있기 때문. s[i][index]의 모든 합을 구해서 문제 입력과 같은지 확인하고 다르면 false를 리턴, 같으면 true 리턴.
import java.util.*;
public class Main {
static int n;
static String str;
static int s[][];
static int res[];
static int sum[];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n=sc.nextInt();
str=sc.next();
res= new int[n];
s = new int[n][n];
sum= new int[n+1];
int index=0;
for(int i=0;i<n;i++) {
for(int j=i;j<n;j++) {
char x = str.charAt(index);
if(x=='-') {
s[i][j]=-1;
}else if(x=='0') {
s[i][j]=0;
}else if(x=='+') {
s[i][j]=1;
}
index++;
}
}
go(0);
for(int i=0;i<n;i++) {
System.out.print(res[i]+" ");
}
}
static boolean go(int index) {
if(index==n)
return true;
for(int i=0;i<=20;i++) {
//0~20까지 반복하면서 res배열에 하나씩 넣어보고, 이때 -10을 해서 -10~10의 구간으로 잡음.
res[index] = i-10;
if(chk(index) && go(index+1))
return true;
//index부터 n까지 진행해보면서 n에 도달하면 true를 반환함.
}
return false;
}
static boolean chk(int index) {
//현재 정한 수들이 부호에 맞는지 확인하는 함수임.
int sum=0;
for(int i=index;i>=0;i--) {
sum+= res[i];
//부호들이 저장된 s[][]배열이랑 i~index까지 부호가 맞는지를
//비교해서 맞으면 true, 다르면 false출력
if(s[i][index]==0 && sum !=0) {
return false;
}if(s[i][index] < 0 && sum >=0) {
return false;
}if(s[i][index]>0 && sum <=0) {
return false;
}
}
return true;
}
}
최백준 선생님의 코딩테스트 기초 강의를 보고 작성한 글입니다.
