
차이를 최대로 (백준 10819번)
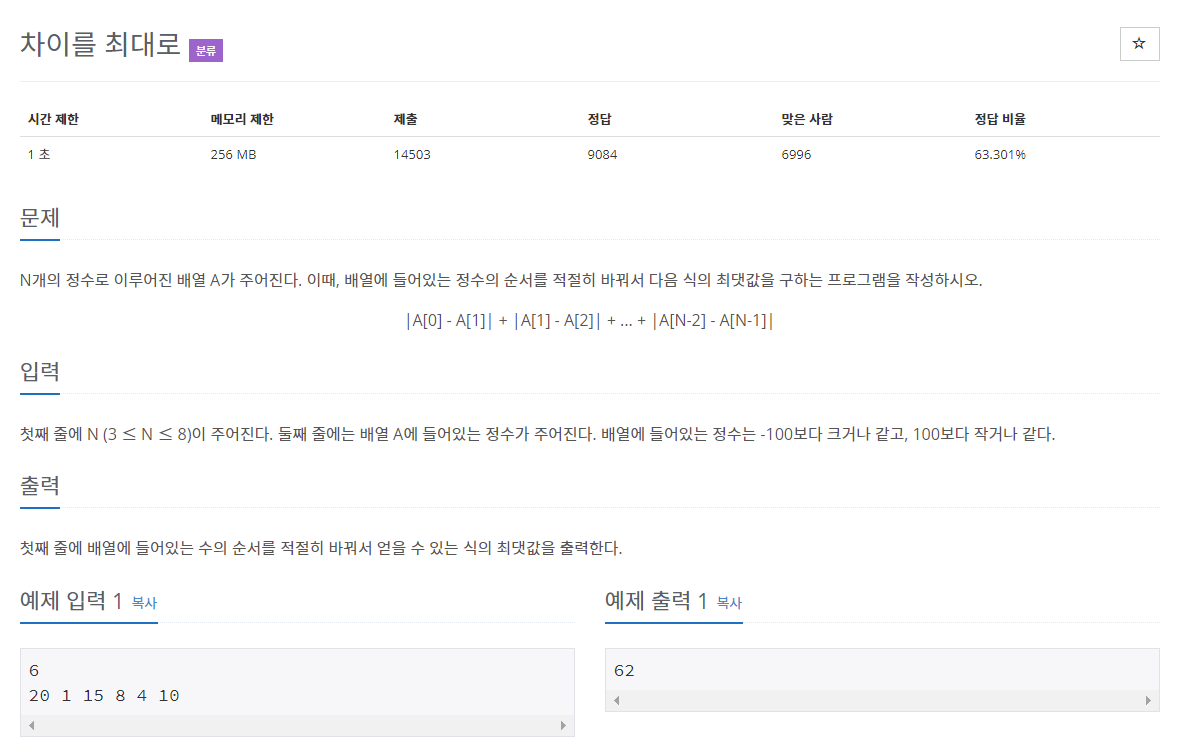
수 N개가 주어졌을 때 (3<=N<=8)
| A[0]-A[1] | + | A[1] - A[2] | + ... + | A[N-2]- A[N-1] | 를 최대로 하는 문제
-
수를 변경할 수는 없음. 하지만 수의 순서를 변경은 가능함.
-
N개의 수가 있을 때 순서를 변경할 수 있는 방법의 수는 ? N!가지
-
8! = 40320개. 모든 경우의 수를 다 해봐도 가능함.
-
첫 순열을 만들고 다음 순열을 호출해주면 됨.
-
시간복잡도는 N! 반복 - 1) 계산 2) 다음 순열을 구함.
-
O(N * N!)
-
첫 순열은 오름차순형태이기 때문에 정렬해주면 됨.
모든 순열을 응용해서 작성하니 금방 끝났다.
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n= sc.nextInt();
int a[]= new int[n];
int res = 0;
for(int i=0; i<n; i++) {
a[i]=sc.nextInt();
}
Arrays.sort(a);
do {
int tmp = cal(a);
res = Math.max(res, tmp);
}while(go(a));
System.out.println(res);
}
public static int cal(int a[]) {
int sum =0;
for(int i=1;i<a.length;i++) {
//절대값 함수를 이용해서 a[i]-a[i-1]의 절대값을 전부 더해줌.
sum += Math.abs(a[i]-a[i-1]);
}
return sum;
}
public static boolean go(int a[]) {
int i=a.length-1;
while(i>0 && a[i-1] >= a[i]) {
i--;
}
if(i<=0) return false;
int j=a.length-1;
while(a[j]<=a[i-1]) {
j--;
}
int tmp=a[i-1];
a[i-1]=a[j];
a[j]=tmp;
j=a.length-1;
while(i<j) {
tmp = a[i];
a[i]=a[j];
a[j]=tmp;
i++;
j--;
}
return true;
}
}
외판원 순회2
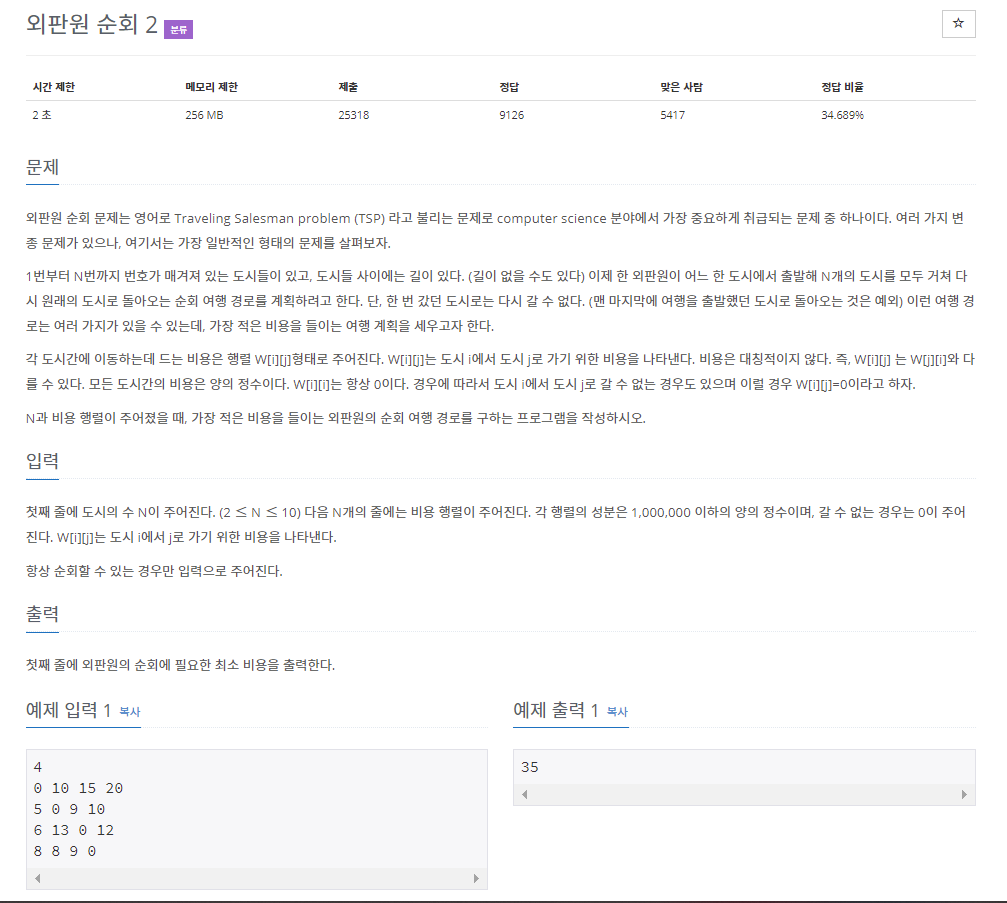
영어로 Travelling Salesman Problem(TSP)
1번부터 N번까지 번호가 매겨져있는 도시가 있다
한 도시에서 시작해 N개의 모든 도시를 거쳐 다시 원래 도시로 돌아오려고 한다.
(한 번 갔던 도시로는 다시 갈 수 없다)
이 때, 가장 적은 비용을 구하는 문제
W[i][j]= i->j비용, 0인 경우는 갈 수 없음.
-
N개 모두 방문 (중복X)
-> 순열 -
모든 순서를 만들어보고 비용을 계산해서 최소값을 구하면 됨.
-
d : 순서
-
d[i] : i번째 방문하는 도시
d[0] d[1] ... d[n-1] -> d[0]
1 2 3 4
2 3 4 1
3 4 1 2
4 1 2 3
위의 4가지는 모두 같은 경우임.
다시 시작한 도시로 돌아가야하기 때문임.
따라서 시작점을 1로 고정해도 된다.
- 전체 방법의 개수는 N!/N가지임. (N-1)!가지
- 시작도시를 한 도시로 고정을 시켜도 문제의 정답을 구하는데는 문제가 없음.
- 시작도시는 1,2,3,4 등 아무거나 해도 상관 없음.
1) N개의 도시를 이용해서 순서를 만들어보면 1로 시작하는거 2로 시작하는거 등등 N으로 시작하는 거 까지 쭉 나옴. 거기서 1로 시작하는 것으로만 구해줌.
2) 전체에 대해서 다음 순열을 구하는 것.
첫 번째 도시가 1이 아니고 2로 변경되는 순간이 왔을 때 탐색을 종료함.
if(d[0] != 1) break; <- 이 조건만 걸어주면 됨. 훨씬 간단함.
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n= sc.nextInt();
int a[][]=new int[n][n];
for(int i=0;i<n;i++) {
for(int j=0; j<n; j++) {
a[i][j]=sc.nextInt();
}
}
int d[]= new int[n];
for(int i=0;i<n;i++) {
d[i]=i;
}
int min = Integer.MAX_VALUE;
do {
if(d[0] != 0) break;
//첫번째가 0이 아니면 break.
boolean chk = true;
int sum=0;
for(int i=0;i<n-1;i++) {
if(a[d[i]][d[i+1]] ==0) {
chk = false;
}else {
sum+= a[d[i]][d[i+1]];
}
}
if(chk && a[d[n-1]][d[0]] != 0) {
sum += a[d[n-1]][d[0]];
if(min > sum) {
min = sum;
}
}
}while(go(d));
System.out.println(min);
}
public static boolean go(int a[]) {
int i=a.length-1;
while(i>0 && a[i-1] >= a[i]) {
i--;
}
if(i<=0) return false;
int j=a.length-1;
while(a[j]<=a[i-1]) {
j--;
}
int tmp=a[i-1];
a[i-1]=a[j];
a[j]=tmp;
j=a.length-1;
while(i<j) {
tmp = a[i];
a[i]=a[j];
a[j]=tmp;
i++;
j--;
}
return true;
}
}문제 이해 하는게 제일 어려운 것 같다^^;;
로또
같은 수가 있어도 순열을 만들 수 있다.
배열에 1,1,2,2,2를 넣고 next_permutation을 수행하면 어떻게 될까,,
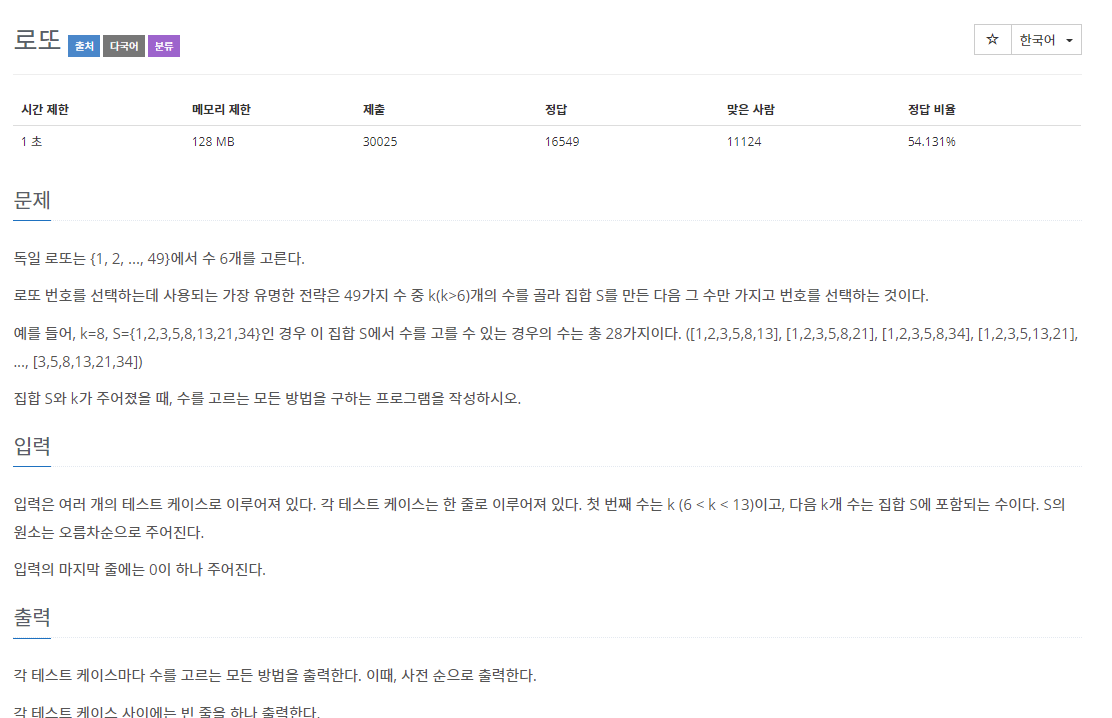
입력으로 주어진 K개의 수 중에서 6개의 수를 고르는 문제
N과 M(2)와 유사한 문제임.
재귀함수를 이용해서 풀면 되지만, 순열을 이용해서도 가능함
- 0이 나오는 것은 고르지 않는 것.
- 1이 나오는 것은 고르는 것.
-> 재귀함수를 이용해서 풀었다.
import java.util.*;
public class Main {
static int k;
static int s[];
static int arr[]=new int[6]; //구해야하는 6개의 수를 담을 배열임
static int len = 6;
public static void main(String[] args) {
Scanner sc= new Scanner(System.in);
while(true) {
k=sc.nextInt();
if(k==0) break;
s= new int[k];
for(int i=0;i<k;i++) {
s[i]=sc.nextInt();
}
go(0,0);
System.out.println();
}
}
static void go(int a, int b) {
if(a==len) { //a가 6과 같아졌을 때 출력.
for(int i=0;i<len;i++) {
System.out.print(arr[i]+" ");
}
System.out.println();
return;
}
//b부터 k까지 계속해서 반복.
for(int i=b;i<k;i++) {
arr[a] = s[i];
go(a+1,i+1);
}
}
}
최백준 선생님의 코딩테스트 기초 강의를 보고 작성한 글입니다.
