
포도주 시식(2156)
포도주가 일렬로 놓여져 있고, 다음과 같은 2가지 규칙을 지키면서 포도주를 최대한 많이 마시려고 한다.
1. 포도주 잔을 선택하면 그 잔에 들어있는 포도주는 모두 마셔야 하고, 마신 후에는 원래 위치에 다시 놓아야 한다.
2. 연속으로 놓여 있는 3잔을 모두 마실 수는 없다.
- i번 포도주의 양 : A[i]
- 1잔, 2잔은 가능. 3잔은 안됨. => 몇잔의 포도주를 연속해서 마셨는가가 중요함.
D[i][j] = i번째 있고 i번 포도주는 j번 연속해서 마신 포도주.
여기서 만약 j=0, 0번 연속해서 포도주를 마신거니까 안 마신 것임.
- D[i][j] = A[1], ... A[i] 까지 포도주를 마셨을 때의 최대양. A[i]는 j번 연속해서 마신 포도주.
- D[i][0] = 0번 연속해서 마신 포도주 -> A[i]를 안마심. A[i-1]는 상관없음.
- D[i][1] = 1번 연속해서 마신 포도주 -> A[i-1]를 안 마심.
- D[i][2] = 2번 연속해서 마신 포도주 -> A[i-1]를 마시고, A[i-2]는 안 마심.
D[i][0] = max(D[i-1][0],d[i-1][1].D[i-1][2]) + 0
D[i][1] = D[i-1][0] + A[i]
D[i][2] = D[i-1][1] + A[i]
> 일차원 배열으로 접근.
- 이친수 방법으로 하면 0,1 이런식으로 해서 0이면 마시지 않고 1이면 마셨음
- D[i] = A[1] , ... A[i]까지 포도주를 마셨을 때, 마실 수 있는 최대양
- 0번 연속해서 마신 포도주 -> A[i]를 마시지 않음. A[i-1]은 마셔도 되고, 안마셔도 됨. => D[i-1]
- 1번 연속 -> A[i]를 마시고, A[i-1]를 마시지 않음. => D[i-2] + A[i]
- 2번 연속 -> A[i-1]를 마시고, A[i-2]는 마시면 안됨. => D[i-3] + A[i-1] + A[i]
=> D[i]= max(D[i-1],D[i-2]+A[i], D[i-3] + A[i-1] + A[i])
초기값 정하는 것
D[1] = A[1]
D[2] = A[1] + A[2]로 미리 처리를 해두고 i=3부터 문제를 푸는 것이 좋다.
=> 초기값 처리가 생각보다 되게 까다롭다..
1차원 배열 코드
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc= new Scanner(System.in);
int n= sc.nextInt();
int a[]= new int[n+1];
for(int i=1;i<=n;i++) {
a[i]=sc.nextInt();
}
int d[] = new int[n+1];
//초기값 설정
d[1] = a[1];
if(n > 1) d[2] = a[1] + a[2];
//초기값 2까지 설정했으니까 3부터 n까지 시작.
for(int i=3; i<=n; i++) {
d[i] = d[i-1];
d[i] = Math.max(Math.max(d[i],d[i-2]+a[i]),d[i-3]+a[i-1]+a[i]);
//위에 말한 식중에 max값을 구해서 d[i]에 넣어줌.
}
int res = d[1];
for(int i=2;i<=n;i++) {
res = Math.max(res, d[i]);
}
System.out.println(res);
}
}2차원 배열 코드
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc= new Scanner(System.in);
int n= sc.nextInt();
int a[]= new int[n+1];
for(int i=1;i<=n;i++) {
a[i]=sc.nextInt();
}
int d[][] = new int[n+1][3];
//초기값 설정
d[1][0] = 0;
d[1][1] = a[1];
d[1][2] = a[1];
for(int i=2; i<=n; i++) {
d[i][0] = Math.max(d[i-1][2], Math.max(d[i-1][1], d[i-1][0]));
d[i][1] = d[i-1][0] + a[i];
d[i][2] = d[i-1][1] + a[i];
}
System.out.println(Math.max(d[n][0], Math.max(d[n][1], d[n][2])));
}
}
=> 미세하게 2차원이 조금 더 빨랐다,,,ㅎㅎ
정수 삼각형(1932)
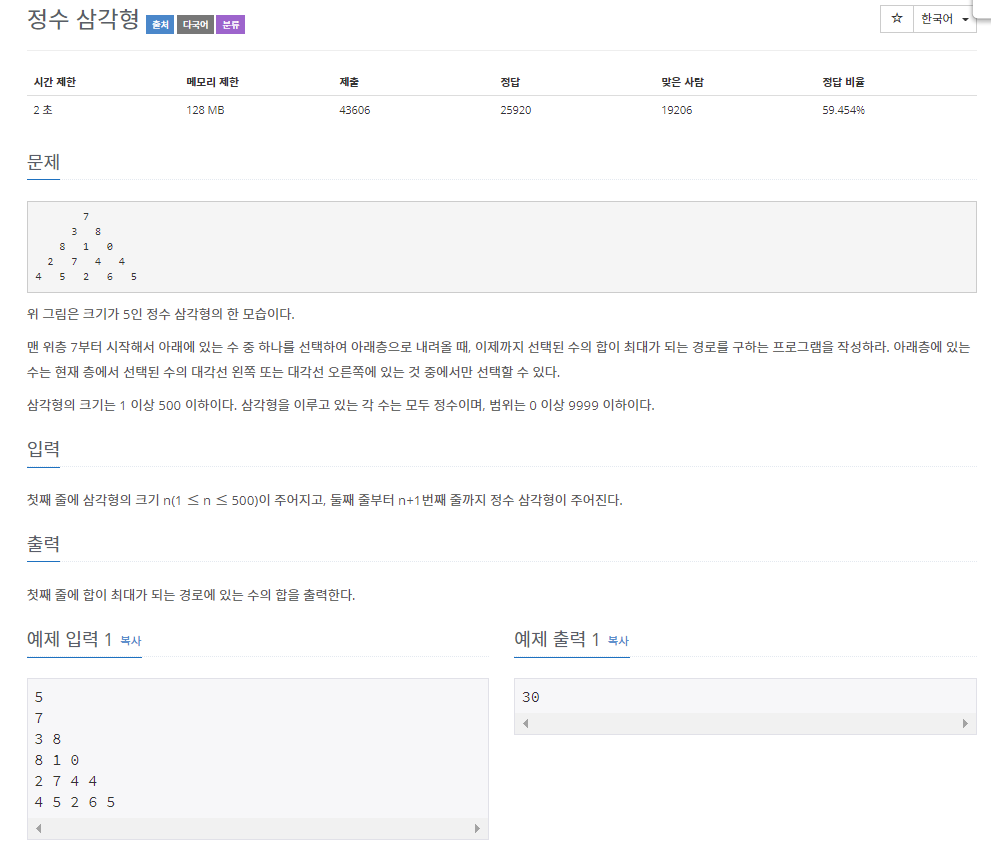
위부터 아래로 이동하면서 그 수의 합의 최대값을 갖는 문제.
아래층으로 내려올 때는 대각선 왼쪽 또는 대각선 오른쪽에 있는 것만 선택할 수 있다.
-
반대로 생각하면 어떤 수가 선택되기 전에 선택된 수는 대각선 왼쪽 위, 오른쪽 위에 있음.
A
B C
D E F
=> B에 오기 전 : A.
D에 오기전 : B
E에 오기전 : B,C
F에 오기전 : C -
D[i][j] = (i,j)에 도착했을 때 구해야 하는 합의 최대값
(i,j)
(i+1,j) (i+1,j+1) -
(i,j)가 선택되기 전에 선택된 수는 (i-1, j),(i-1,j-1) 중 하나다.
-> 따라서 D[i][j]= max(D[i-1][j],D[i-1][j-1]) + A[i][j]
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc= new Scanner(System.in);
int n= sc.nextInt();
int a[][]= new int[n][n];
int d[][] = new int[n][n];
for(int i=0;i<n;i++) {
for(int j=0; j<=i; j++) {
a[i][j] = sc.nextInt();
}
}
d[0][0] = a[0][0];
for(int i=1; i<n;i++) {
for(int j=0;j<=i;j++) {
d[i][j]= Math.max(d[i-1][j], d[i-1][j-1]) + a[i][j];
}
}
int res = d[n-1][0];
for(int i=0;i<n;i++) {
res = Math.max(res , d[n-1][i]);
}
System.out.println(res);
}
} => 아무 생각 안하고 math.max로 작성했는데 음수값이 있다는 것을 간과했다,, ArrayIndexOutOfBoundsException 발생..
코드
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc= new Scanner(System.in);
int n= sc.nextInt();
int a[][]= new int[n][n];
int d[][] = new int[n][n];
for(int i=0;i<n;i++) {
for(int j=0; j<=i; j++) {
a[i][j] = sc.nextInt();
}
}
d[0][0] = a[0][0];
for(int i=1; i<n;i++) {
for(int j=0;j<=i;j++) {
//j-1이 0보다 작으면 존재하지 않으니까 우선 그냥 다 j로 넣음.
d[i][j] = d[i-1][j] + a[i][j];
//여기서 j-1이 0보다 크거나 같으면서 뒤에 오는 값이 더 클 때만 대입.
if (j-1 >= 0 && d[i][j] < d[i-1][j-1] + a[i][j]) {
d[i][j] = d[i-1][j-1] + a[i][j];
}
}
}
int res = d[n-1][0];
for(int i=0;i<n;i++) {
res = Math.max(res, d[n-1][i]);
}
System.out.println(res);
}
} 가장 큰 증가하는 부분 수열(11055)
수열 A가 주어졌을 때, 그 수열의 증가 부분 수열 중에서 합이 가장 큰 것을 구하는 문제.
- 가장 긴 증가하는 부분 수열 : D[i] = i번까지 있을 때 길이. ( j<i, A[j] < A[i]) => max(D[j]) + 1
- 가장 큰 증가하는 부분 수열 : D[i] = i번까지 있을 때 최대 합. => max(D[j]) + A[i]
코드
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc= new Scanner(System.in);
int n= sc.nextInt();
int a[] = new int[n];
int d[] = new int[n];
for(int i=0;i<n;i++) {
a[i]= sc.nextInt();
}
for(int i=0;i<n;i++) {
d[i]=a[i];
for(int j=0;j<i;j++) {
if(a[j] < a[i] && d[i] < d[j]+a[i])
d[i]=d[j] + a[i];
}
}
int res = d[0];
for(int i=0; i<n;i++) {
res = Math.max(res, d[i]);
}
System.out.println(res);
}
} 가장 긴 감소하는 부분수열(11722)
수열 A가 주어졌을 때, 그 수열의 감소하는 부분 수열 중에서 가장 긴 것을 구하는 문제.
2가지 방법이 있다.
입력으로 주어진 수열 A를 뒤집어서 가장 긴 증가하는 부분 수열을 구하는 방법.
가장 긴 증가하는 부분 수열과 비슷하게 구하는 방법 (뒤에서부터 구해야 한다)
- 가장 긴 증가하는 부분 수열에서 D[i]=A[i]에서 끝나는 LIS
- 가장 긴 감소하는 부분 수열에서 D[i]=A[i]에서 끝나는 가장 긴 감소하는 부분 수열의 길이. (j<i, A[j]>A[i])
D[i] = max(D[j]) + 1 (j < i && A[j] > A[i])
코드
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc= new Scanner(System.in);
int n= sc.nextInt();
int a[] = new int[n];
int d[] = new int[n];
for(int i=0;i<n;i++) {
a[i]= sc.nextInt();
}
for(int i=0;i<n;i++) {
d[i]= 1;
for(int j=0;j<i;j++) {
if(a[j] > a[i] && d[i] < d[j]+1)
d[i]=d[j] + 1;
}
}
int res = d[0];
for(int i=0; i<n;i++) {
res = Math.max(res, d[i]);
}
System.out.println(res);
}
} => 초기값과 부등호 기호와 몇가지만 바꿔주면 된다.
다른 방식 풀이
D[i]=A[i]에서 시작하는 가장 긴 감소하는 부분 수열의 길이
D[i] = max(D[j]) + 1 ( i<j && A[i] > A[j] )
뒤에서부터 for문으로 돌리면 됨.
가장 긴 바이토닉 부분 수열(11054)
수열 A가 주어졌을 때, 그 수열의 바이토닉 부분 수열 중에서 가장 긴 것을 구하는 문제.
-
바이토닉 수열이란 ? 10, 20, 30, 25, 20 처럼 증가하다가 감소하는 수열을 뜻함.
-
i번째에서 끝나는 가장 긴 증가하는 부분 수열의 길이 -> i -> i번째에서 시작하는 가장 긴 감소하는 부분 수열의 길이.
즉, 가장 긴 증가하는 부분 수열의 길이와 가장 긴 감소하는 부분 수열의 길이를 전부 구함.
- 총 길이를 구한 다음 -1를 해주면 됨. A[i]는 2번 겹치기 때문.
코드
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc= new Scanner(System.in);
int n= sc.nextInt();
int a[] = new int[n];
int d[] = new int[n];
int d2[] = new int[n];
for(int i=0;i<n;i++) {
a[i] = sc.nextInt();
}
//증가
for(int i=0;i<n;i++) {
d[i]=1;
for(int j=0;j<i;j++) {
if(a[j] < a[i] && d[i] < d[j] + 1) {
d[i] = d[j]+1;
}
}
}
//감소
for(int i=n-1;i>=0;i--) {
d2[i]=1;
for(int j=i+1;j<n;j++) {
if(a[j] < a[i] && d2[i] < d2[j] + 1) {
d2[i] = d2[j]+1;
}
}
}
int res= d[0]+d2[0]-1;
for(int i=0;i<n;i++) {
res = Math.max(res, d[i]+d2[i]-1);
}
System.out.println(res);
}
} 연속합2 (13398)
수열의 연속합 중 가장 큰 합을 구하는 문제
수는 하나 제거할 수 있다. 제거하지 않아도 된다. => 이 조건이 추가되었음.
- 원래 연속합 D[i] = A[i]에서 끝나는 최대 연속합. = max(D[i-1] + A[i] , A[i])
- 시간복잡도는 O(N)이었음.
바이토닉 수열을 했던 것 처럼 원리를 이용함.
- D[i] = i번째에서 끝나는 최대 연속합
- D2[i] = i번째에서 시작하는 최대 연속합
i-1 / i / i+1
-> 여기서 i를 제거하면 i-1과 i+1를 연결시킬 수 있음!
=> 각각의 수를 제거할 때마다 D[i-1] + D2[i+1]의 값을 구해서 MAX를 비교해주기만 하면 됨. ( 지우는 수는 2<= i < =n-1)
- 시간복잡도 O(N)만에 해결 가능함.
코드
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc= new Scanner(System.in);
int n= sc.nextInt();
int a[] = new int[n];
int d[] = new int[n];
int d2[] = new int[n];
for(int i=0;i<n;i++) {
a[i] = sc.nextInt();
}
for(int i=0;i<n;i++) {
d[i]=a[i];
if(i>0 && d[i] < d[i-1] + a[i]) {
d[i] = d[i-1] + a[i];
}
}
for(int i=n-1;i>=0;i--) {
d2[i]=a[i];
if(i < n-1 && d2[i] < d2[i+1] +a[i]) {
d2[i] = d2[i+1] + a[i];
}
}
int res= d[0];
for(int i=1;i<n;i++) {
res = Math.max(res, d[i]);
}
// 수를 빼지않고 더한 연속합.
for(int i=1;i<n-1;i++) {
res = Math.max(res, d[i-1] + d2[i+1]);
}
// 수를 빼고나서 더한 연속합과 빼지않고 더한 연속합을 비교해서 max값 대입
System.out.println(res);
}
} 타일 채우기(2133)
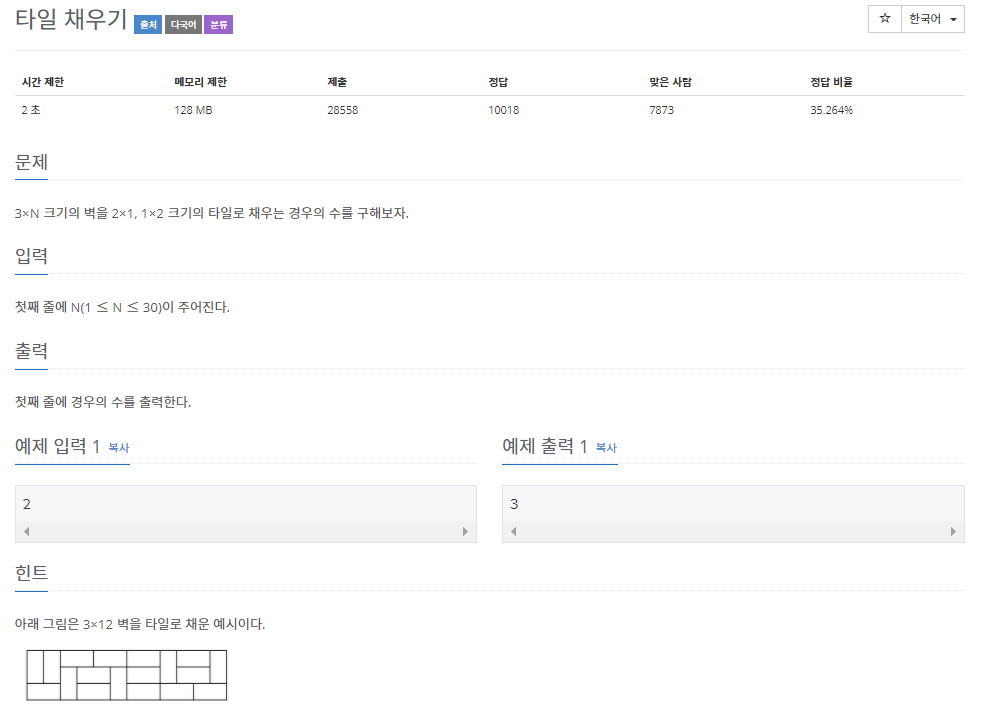
3 x N을 1 X 2, 2 X 1로 채우는 방법의 수
D[i] = 3 x i를 채우는 방법의 수.
마지막에 올 수 있는 가능한 경우의 수.
코드
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc= new Scanner(System.in);
int n= sc.nextInt();
long d[] = new long[n+1];
d[0] = 1;
for(int i=2; i<=n; i+=2) {
d[i] = d[i-2] * 3;
for(int j=i-4; j>=0; j-=2) {
d[i] += d[j] * 2;
}
}
System.out.println(d[n]);
}
} 최백준 선생님의 코딩테스트 기초 강의를 보고 작성한 글입니다.
