[Algorithm] 2-3 Insertion Sort(삽입 정렬)

정렬 알고리즘
1. Bubble Sort(거품 정렬)
2. Selection Sort(선택 정렬)
3. Insertion Sort(삽입 정렬) ⇠
4. Quick Sort(퀵 정렬)
5. Merge Sort(병합 정렬)
6. Heap Sort(힙 정렬)
7. Radix Sort(기수 정렬)
8. Counting Sort(계수 정렬)

기본 개념

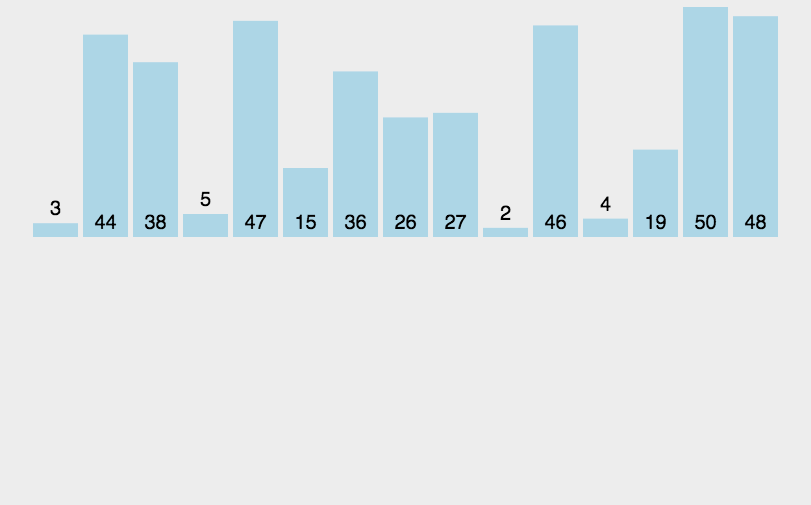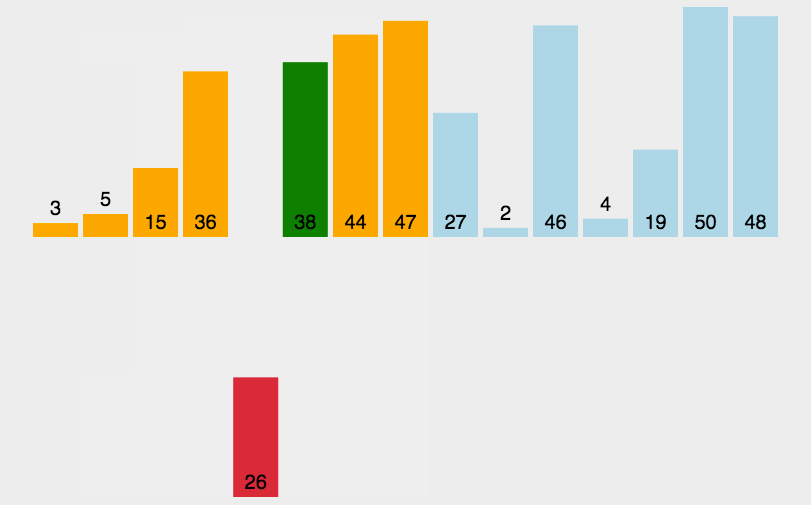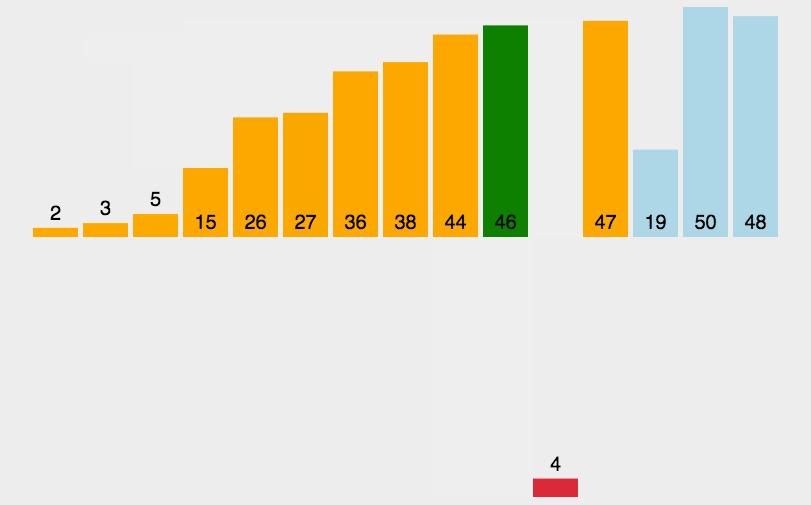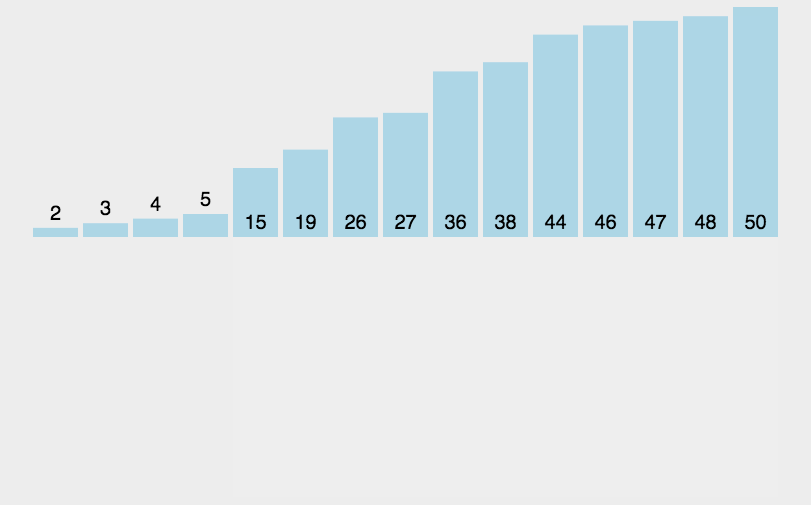
• 손 안의 카드를 정렬하는 방법과 유사하다.
• Selection Sort와 유사하지만 조금 더 효율적인 정렬 알고리즘이다.
• 2번째 원소부터 시작하여 그 앞(왼쪽)의 원소들과 비교하여 삽입할 위치를 지정한 후, 원소를 뒤로 옮기고 지정된 자리에 자료를 삽입하여 정렬하는 알고리즘이다.
• 최선의 경우 O(N)이라는 빠른 효율성을 가지고 있어, 다른 정렬 알고리즘의 일부로 사용될 만큼 좋은 정렬 알고리즘이다.

특징

• 선택/거품 정렬은 한 패스가 끝날수록 탐색 범위가 줄어들지만 삽입 정렬은 오히려 정렬 범위가 넓어진다.
• 큰 그림에서 보았을 때 바깥 쪽 루프는 순방향, 안 쪽 루프는 역방향으로 진행되고 있다.

구현(Java)

public class Insertion {
	public static void sort(int[] arr) {
    	// 1. 2번째 위치부터 시작
    	for (int i = 1; i < arr.length; i++) {
        	// 2. temp와 이전에 있는 원소들과 비교하며 삽입해 나간다.
        	int temp = arr[i];
            int prev = i - 1;
            while ((prev >= 0) && (arr[prev] > temp)) {
            	arr[prev+1] = arr[prev];
                prev--;
            }
            arr[prev+1] = temp;
        }
    }
}

복잡도

• 공간복잡도 : 별도의 추가 공간을 사용하지 않고 주어진 배열이 차지하고 있는 공간 내에서 값들의 위치만 바꾸기 때문에 O(1) 의 공간 복잡도를 가진다.
• 시간복잡도 : 루프문을 통해 정렬 범위를 2개로 시작해서 전체로 확장해야 하기 때문에 기본적으로 O(N) 의 시간을 소모하며, 각 패스에서는 정렬 범위에 새롭게 추가된 값과 기존 값들의 대소 비교 및 자리 교대를 위해서 O(N) 의 시간을 필요로 하게 된다. 따라서, 총 O(N^2) 의 시간 복잡도를 가진다.

최적화를 통해 부분적으로 정렬된 배열에 대해서 성능을 개선할 수 있다. 특히, 완전히 정렬되어 있는 경우 O(N) 까지 시간 복잡도를 향상시킬 수 있다.
기존에 있던 값들은 이전 패스에서 모두 정렬되었다는 점을 활용하면 불필요한 비교 작업을 제거할 수 있다.
예를 들어, [1,2,3,5] 에 4 가 추가된다면 5와는 swap이 필요하지만 3은 swap이 필요하지 않는다. 3앞에 있는 숫자들은 이전에 정렬을 통해서 3보다 작다는 걸 알기 때문에 앞에 있는 숫자들은 비교하지 않는다.
이 사실을 이용해 새롭게 추가된 값보다 작은 숫자를 만나는 최초의 순간까지만 내부 반복문을 수행하면 된다.