[Algorithm] 에라토스테네스의 체

기본 개념

소수가 되는 수의 배수를 지우면 남은 건 소수가 된다.

소수가 무엇인지를 찾을 필요가 없으며 2부터 자기 자신을 제외한 배수가 되는 것을 지우면 됩니다.

1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다.
2. 소수가 되는 수의 배수를 지우면 남은 건 소수이다.
3. 2로 예를 들자면 자기 자신을 제외한 2의 배수를 지운다.
4. 3도 2처럼 3 자기 자신을 제외한 3의 배수들을 지운다.
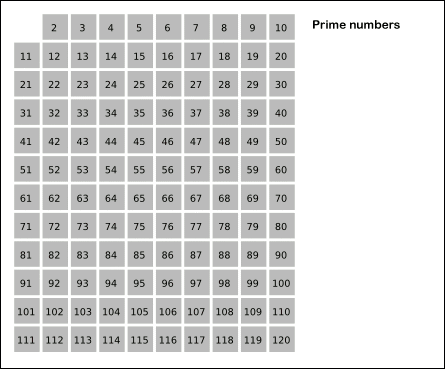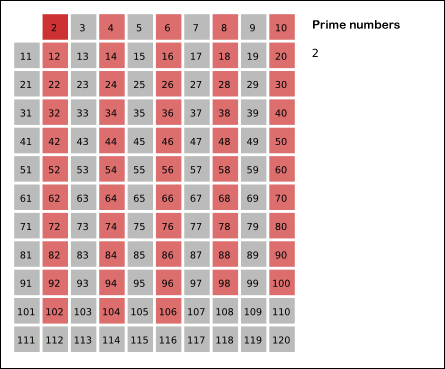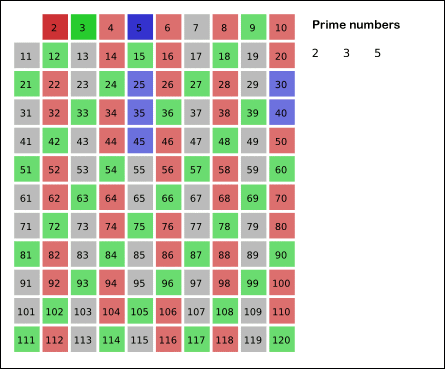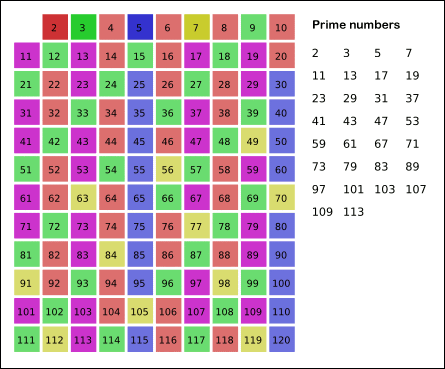
5. 특정 숫자만큼 이 과정을 반복한다.

구현

public class Solution {

	// 예제와 같이 120까지의 소수를 구하기 위해 120 선언.
	static boolean prime[] = new boolean[4000001];
	static ArrayList<Integer> prime_numbers = new ArrayList<>();
    
    public static void main(String[] args) throws Exception{
		
		// 구하고자 하는 숫자 범위
        int N = 4000000;
        
        // 소수는 false
        // 1은 소수가 아니므로 제외
        prime[0] = prime[1] = true;
        
        // 제곱근까지 하는 이유 : 제곱근보다 큰 숫자의 배수 중 아직 체크가 안된 수는 N보다 크게 될 수 밖에 없다.
        for(int i=2; i*i<=N; i++){
        	// prime[i]가 소수라면
            if(!prime[i]){
            	// prime[j] 소수가 아닌 표시
            	// i*i 인 이유 : i*1, i*2, ..., i*(i-1)는 이미 이전 루프문에서 검사했다.
            	for(int j=i*i; j<=N; j+=i) prime[j]=true;                
            }        
        }    
        
        // 소수 출력
        for(int i=1; i<=N;i++){
        	if(!prime[i]) prime_numbers.add(i);     
        }
        
        // 4000000까지 소수 개수
        System.out.println(prime_numbers.size());
        // 소수 확인 
        for(int i=1; i<=10; i++) {
        	System.out.println(prime_numbers.get(i));
        }
        
    }
}