[Algorithm] 1-1 완전탐색 - Permutation(순열)

순열 (Permutation)

서로 다른 n개 중 r개를 중복 없이 골라 순서대로 나열하는 것(정렬이 되어 있음)

$nPr = n \times (n-1) \times (n-2)\ \cdot\cdot\cdot \times\ (n-r+1)$

✔️ 모든 경우의 수를 계산하는 완전 탐색에서 사용하는 알고리즘

예시

{1,2,3} 에서 3개를 뽑는 경우의 수

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

{1,2,3} 에서 2개를 뽑는 경우의 수

1 2
1 3
2 1
2 3
3 1
3 2

순열 구현 방식

1. Swap을 이용한 순열
2. Visited 배열을 이용한 순열
   
   

1. Swap을 이용한 순열

✔️ swap 함수를 만들어서 배열들의 값을 직접 바꾸는 방법

✔️ 배열의 첫 값부터 순서대로 하나씩 바꾸며 모든 값을 한번씩 swap

과정

1. 0번째 인덱스 원소를 0번째 부터 n-1번째까지 위치를 바꾼다. (ABC, BAC, CBA)
2. 1번 과정을 진행해서 나온 경우들을, 1번째 인덱스 원소를 1번째부터 n-1번째까지 위치를 바꾼다.
3. 이러한 과정을 n-1번 반복한다.
   
   

주의할 점

순열들의 순서가 보장되지 않는다.

ex) C,A,B가 먼저 나오는게 아니라 C,B,A가 먼저 나옴

구현

public void permutation(int[] arr, int n, int r, int depth) {
	if(depth == r){
    	doSomething();     	                 // 마지막 요소까지 도달하였으므로 종료
        return;
    }
    
    for(int i=depth; i<n; i++){
    	swap(arr, depth, i);                 // 현재 인덱스와 depth에 해당하는 요소를 swap
        permutation(arr, n, r, depth+1);     // depth를 한칸 이동시키고 swap 
        swap(arr, depth, i);                 // 원래대로 돌림
    }
}

public void swap(int[] arr, int depth, int i){
	int temp = arr[depth];
	arr[depth] = arr[i];
	arr[i] = temp;
}

2. Visited 배열을 이용한 순열

✔️ visited 배열을 이용

✔️ 사전식으로 순열 구현 가능

✔️ DFS로 구현

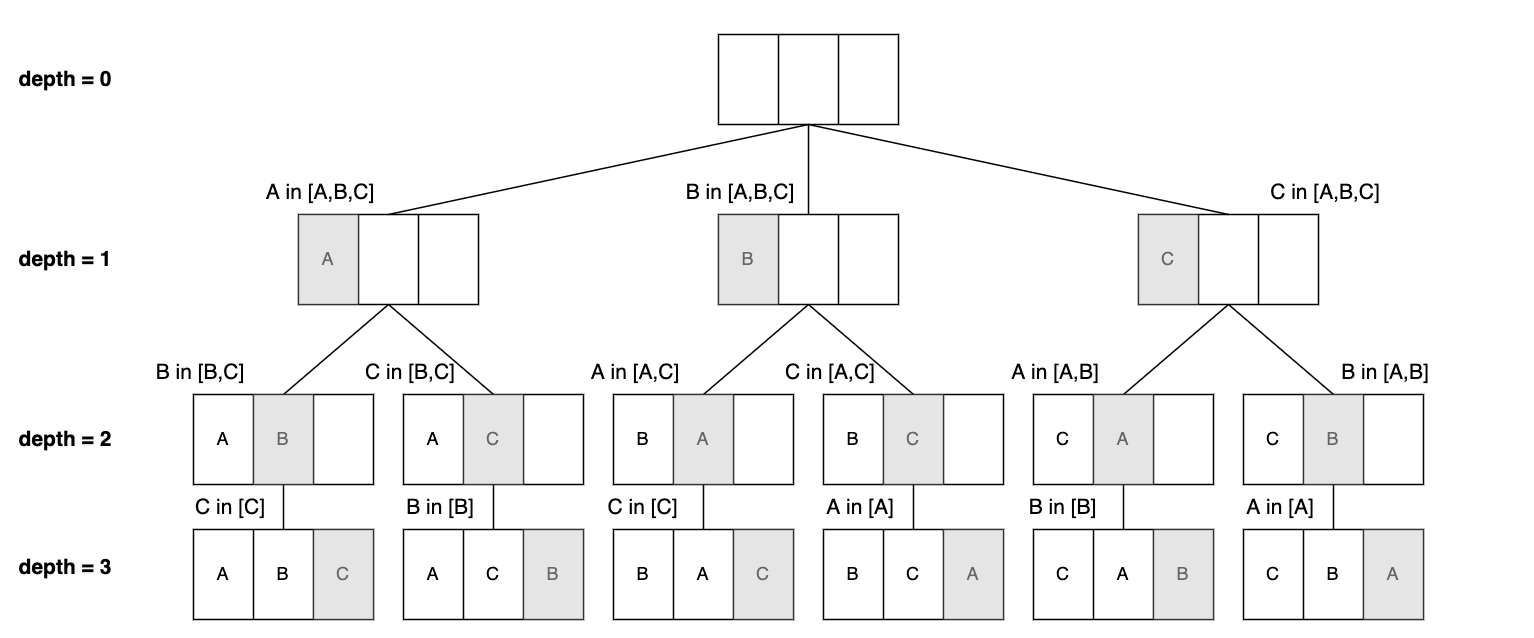
과정

1. DFS를 돌면서 모든 인덱스에 방문해 output 배열에 값을 넣는다
2. 이미 들어간 값은 visited를 true로 변경해서 중복해서 값이 들어가지 않도록 한다
3. 이러한 과정을 depth가 r 값과 같아질 때까지 반복한다
   
   

구현

static void perm(int[] arr, int[] output, boolean[] visited, int depth, int n, int r) {
    if (depth == r) {                                      // depth가 r이 되면 종료
        print(output, r);
        return;
    }
 
    for (int i=0; i<n; i++) {
        if (visited[i] != true) {
            visited[i] = true;                            // 방문처리
            output[depth] = arr[i];
            perm(arr, output, visited, depth + 1, n, r);       
            visited[i] = false;                           // 방문해제
        }
    }
}

시간 복잡도

$O(n!)$

✔️ $nPr$이기 때문