[영상처리] 이미지 보간법

✏️ 이미지 보간법(Image Interpolation)이란?

이미지에 변형을 줄 때 픽셀과 픽셀 사이의 값을 채워주는 것을 이미지 보간 이라고 한다.

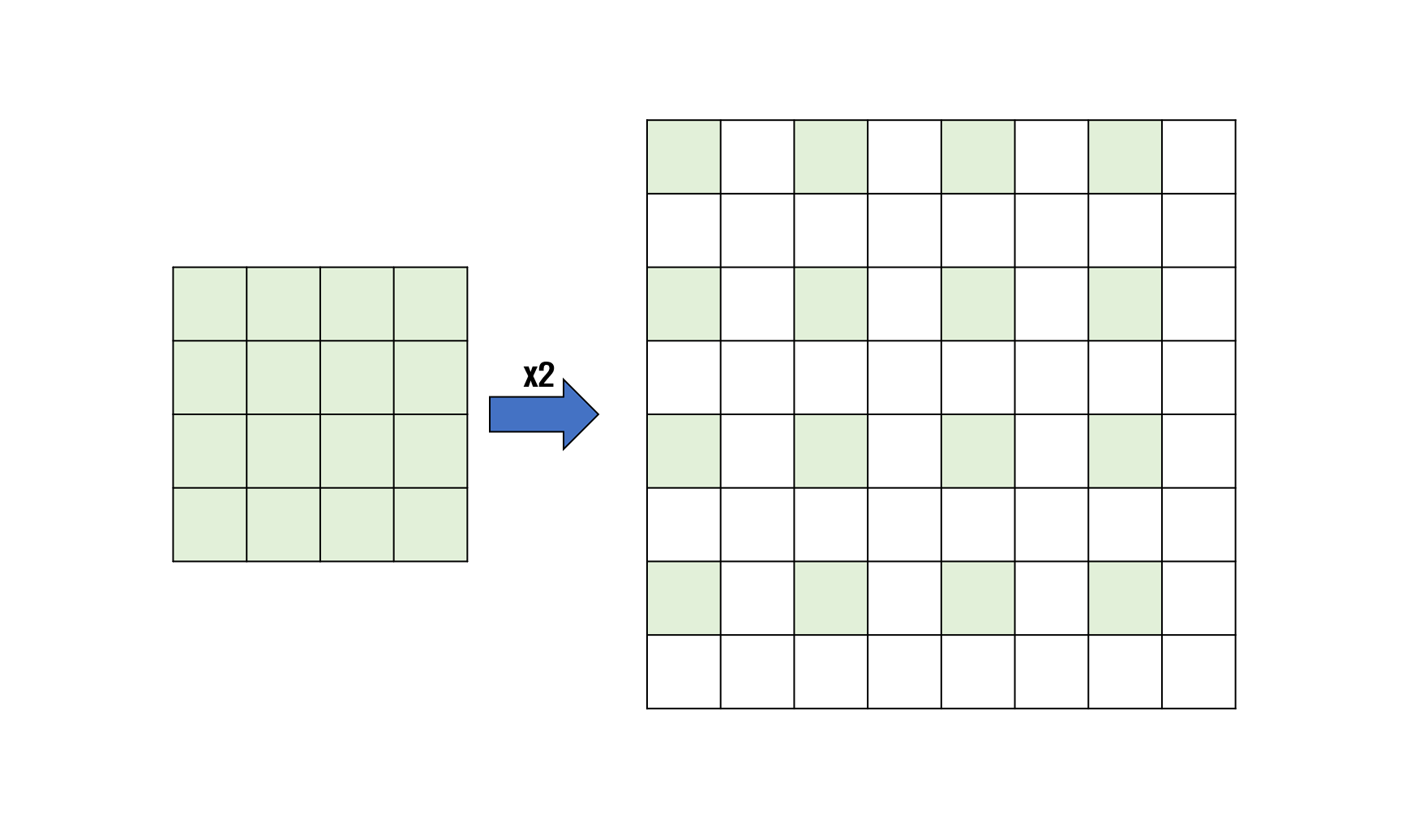
사진과 같이 이미지 크기를 키우면 사이에 비어있는 값을 채워야 한다.

이미지 보간법의 종류

• 최근접 보간법
• 이중선형보간법(Bilinear Interpolation)
• 3차원 스플라인 보간법(Bicubic Spline Interpolation)

이미지는 2차원 형태로 x축 y축 이 존재한다. 먼저 1차원에서의 보간법의 원리에 대해 알아보고 후에 이미지에 적용시켜 볼 것이다.

---

✏️ 최근접 보간법(Nearest Neighbor Interpolation)

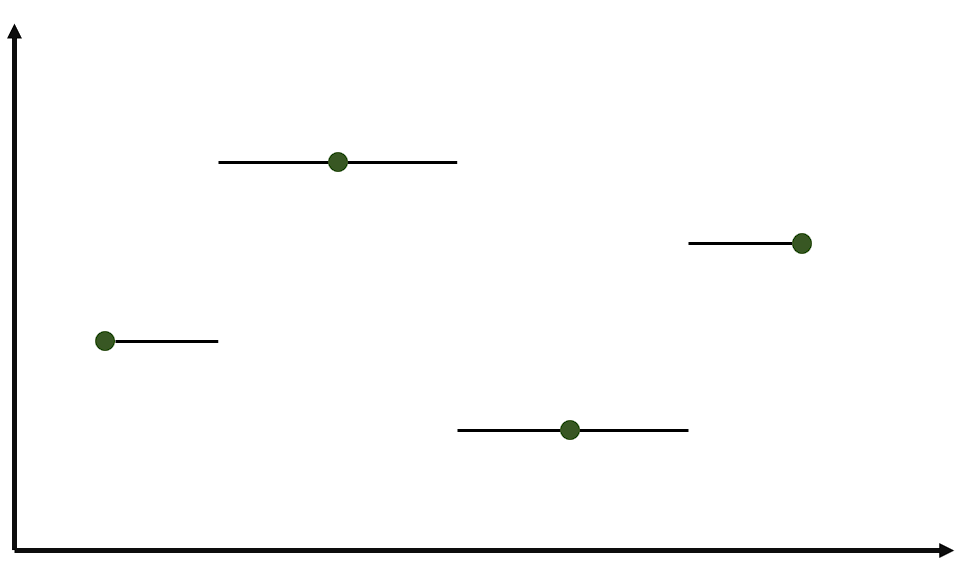
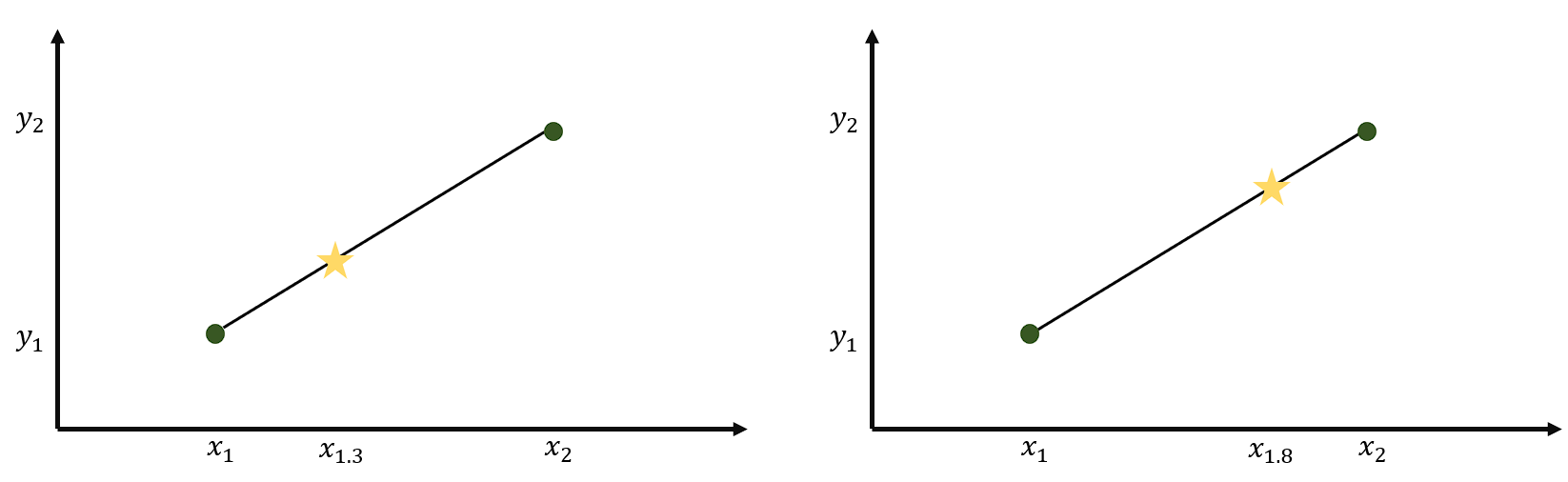
그래프과 같이 주변값에 가장 가까운 값으로 채워주는 방식이다. $x_{1}$과 $x_{2}$의 거리가 1이라고 가정하면 $x_{1.3}$은 $y_{1}$의 값을 가지고 $x_{1.8}$는 $y_{2}$의 값을 가진다. $x$값이 실수라고 생각한다면 반올림의 개념을 생각할 수 있다.

---

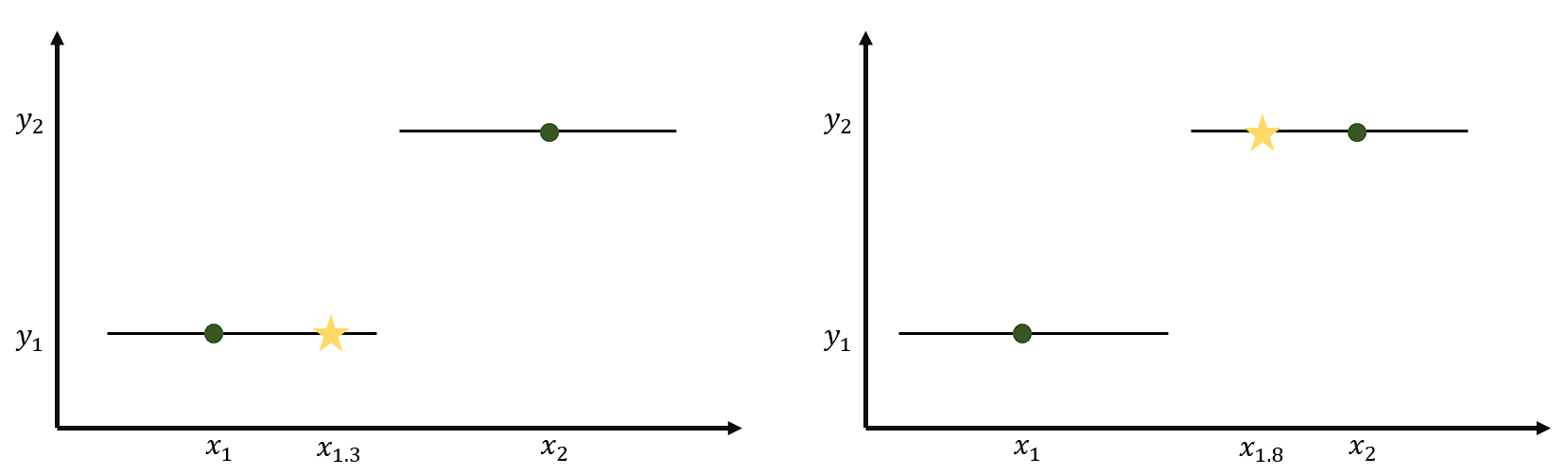
✏️ 선형 보간법(Linear Interpolation)

1차 선형 함수를 통해 사잇값을 추정하는 방식이다.

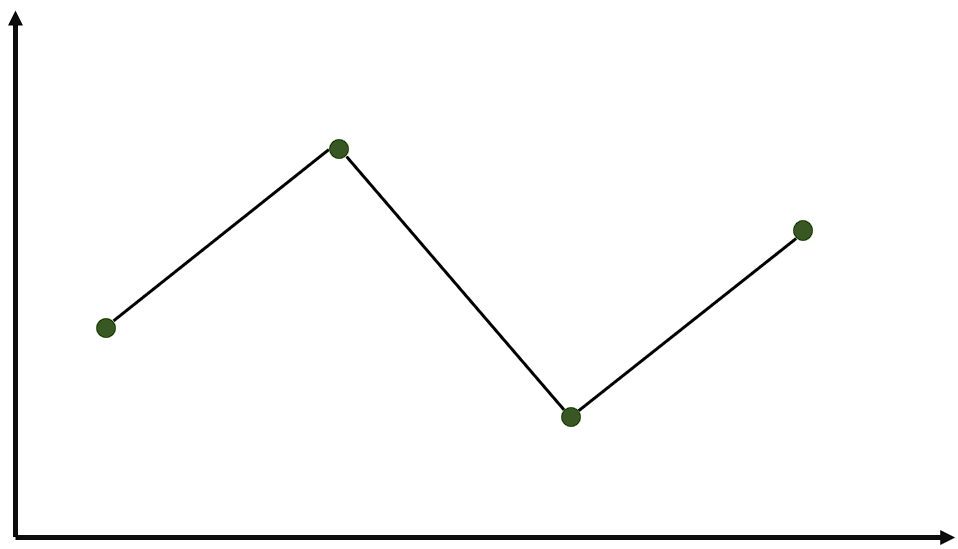
1차 선형 함수를 통해 사잇값을 추정하는 방식이다. 그래프와 같이 각 값을 단순히 직선으로 이어줘 각 함수가 일차함수의 형태를 가진다.

$x_{1.3} = x_{1}*\frac{x_{1.3}-x_{1}}{x_{2}-x_{1}}+x_{2}*\frac{x_{2}-x_{1.3}}{x_{2}-x_{1}}$

단순 직선으로 이루어져 있어 내분점 구하는 공식처럼 계산해도 된다.
다른 방법으로는 두점사이사이 마다 일차 함수식을 구하여 $x$값을 대입해도 된다.

---

✏️ 3차 스플라인 보간법(Cubic Spline Interpolation)

3차 함수를 통해 사잇값을 추정하는 방식

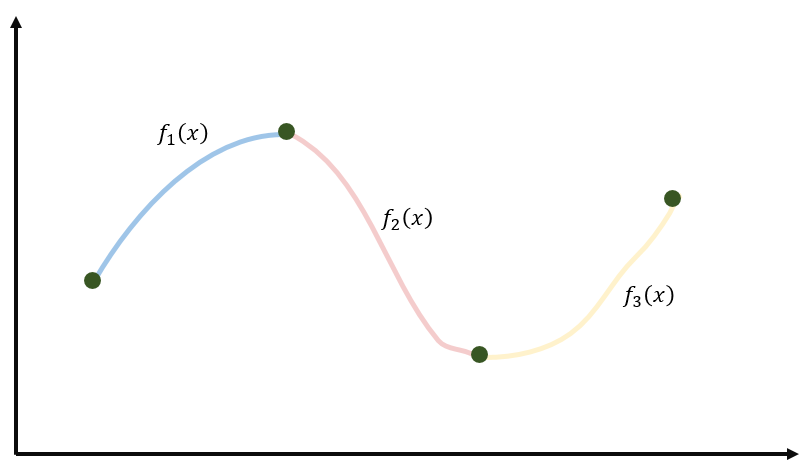
$x_i < x < x_{i+1}$ 를 만족하는 모든 점에서 $f_i$함수는 아래 식에 해당한다.
$\begin{cases} f_{i}(x)=a_i(x-x_i)^3+b_i(x-x_i)^2+c_i(x-x_i)+d_i \\ f'_{i}(x)=3a_i(x-x_i)^2+2b_i(x-x_i)+c_i\\ f''_{i}(x)=6a_i(x-x_i)+2b_i \\ \end{cases}$

스플라인 함수의 조건
1. 함수값은 내부 절점에서 같아야 한다.
2. 첫번째와 마지막 함수는 양 끝점을 통과해야 한다.
3. 내부 절점에서 1차 도함수가 같아야 한다.
4. 내부 절점에서 2차 도함수가 같아야 한다.
5. 양끝에서 2차 도함수가 0이라고 가정한다. (혹은 값을 주어주어야 한다.)

1번조건
각 점에서 연속이기 위해 함수값이 같아야 한다.
$f_{i}(x_i)=f_{i-1}(x_{i})$

2번조건
$f_{0}(x_0)=y_0$
$f_{n-1}(x_{n})=y_n$

3번조건
$f'_{i}(x_i)=f'_{i-1}(x_{i})$

4번조건
$f''_{i}(x_i)=f''_{i-1}(x_{i})$

5번조건
$f''_{0}(x_0)=0$
$f''_{n-1}(x_{n})=0$

위 조건을 이용해서 $f_i(x)$ 함수를 구할 것 이다.

먼저 $f_i$와 $f'_i$에 $x_i$를 대입한다.

$\begin{cases} f_i(x_{i})=a_i(x_{i}-x_i)^3+b_i(x_{i}-x_i)^2+c_i(x_{i}-x_i)+d_i =d_i= y_i\\ f'_i(x_{i})=3a_i(x_{i}-x_i)^2+2b_i(x_{i}-x_i)+c_i=c_i=D_i\\ \end{cases}$

$d_i = y_i$를 구한다. 이때 $f_i'(x_i)=D_i$로 둔다. $c_i=D_i$이다.

이제 $a_i$와 $b_i$를 구해야 한다.
두 값을 구하기 위해 필요한 $f_i(x_{i+1})$과 $f'_i(x_{i+1})$를 구해 연립한다.
$f_i(x_{i+1})=a_i(x_{i+1}-x_i)^3+b_i(x_{i+1}-x_i)^2+c_i(x_{i+1}-x_i)+d_i$
$f'_i(x_{i+1})=3a_i(x_{i+1}-x_i)^2+2b_i(x_{i+1}-x_i)+c_i=D_{i+1}$이고 $c_i=D_i$를 대입해주면
$3a_i(x_{i+1}-x_i)^2+2b_i(x_{i+1}-x_i) = D_{i+1}-D_i$의 식이 나오게 된다.
앞서 구한 두 식을 연립하면

$\begin{cases} 3a_i(x_{i+1}-x_i)^2+2b_i(x_{i+1}-x_i) = D_{i+1}-D_i\\ y_{i+1}=a_i(x_{i+1}-x_i)^3+b_i(x_{i+1}-x_i)^2+c_i(x_{i+1}-x_i)+y_i \end{cases}$

$a_i=\frac{2(y_i-y_{i+1})}{(x_{i+1}-x_i)^3}+\frac{D_{i+1}+D_i}{(x_{i+1}-x_i)^2}$

$b_i=\frac{3(y_{i+1}-y_{i})}{(x_{i+1}-x_i)^2}-\frac{D_{i+1}+2D_i}{(x_{i+1}-x_i)}$

이다.

---

✏️ 이미지 보간 예시

최근접 보간법

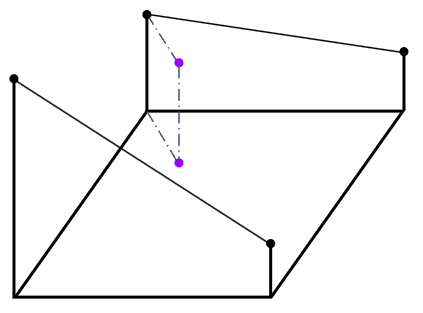
위 사진과 같이 특정 점에서 가장 가까운 좌표의 픽셀 값으로 보간이 이루어진다.

이중선형보간법(Bilinear Interpolation)

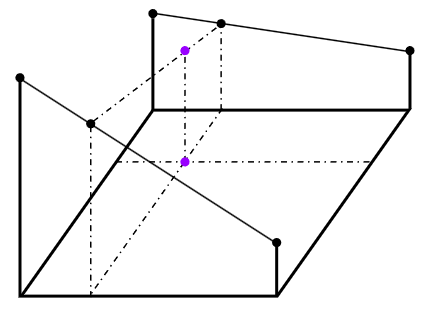
3차 스플라인 보간법(Bicubic Spline Interpolation)

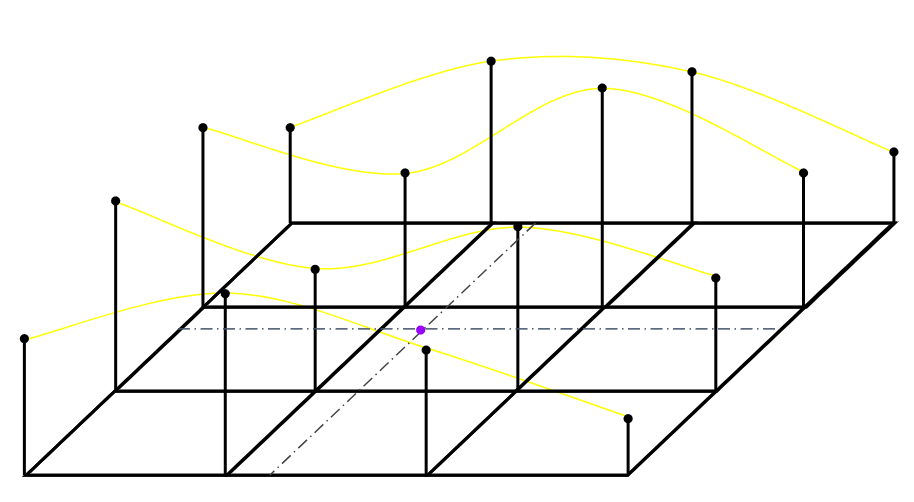
4개의 점을 이용해 스플라인 보간을 진행한다. 구하려는 좌표 기준 $y$축 위아래 4개의 라인을 구해준다.

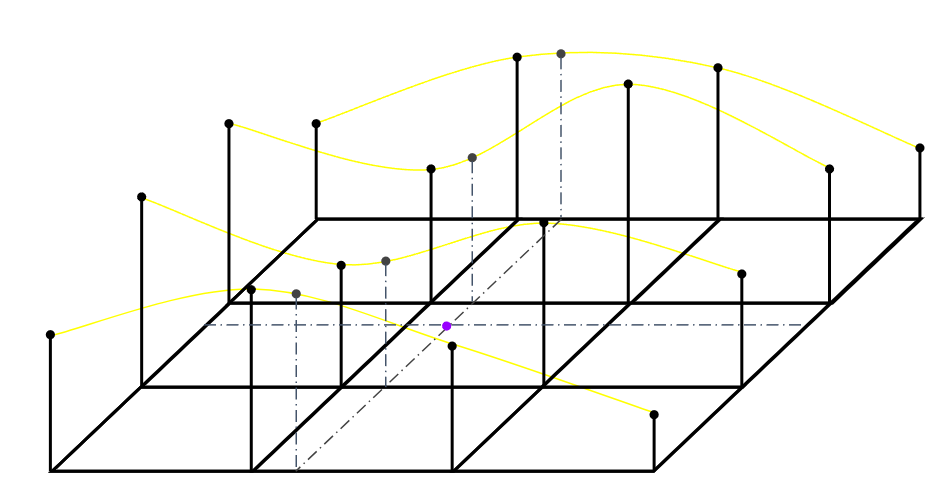
해당하는 4개의 선에서 구하고자 하는 $x$값에 해당하는 4개의 값을 구해준다.

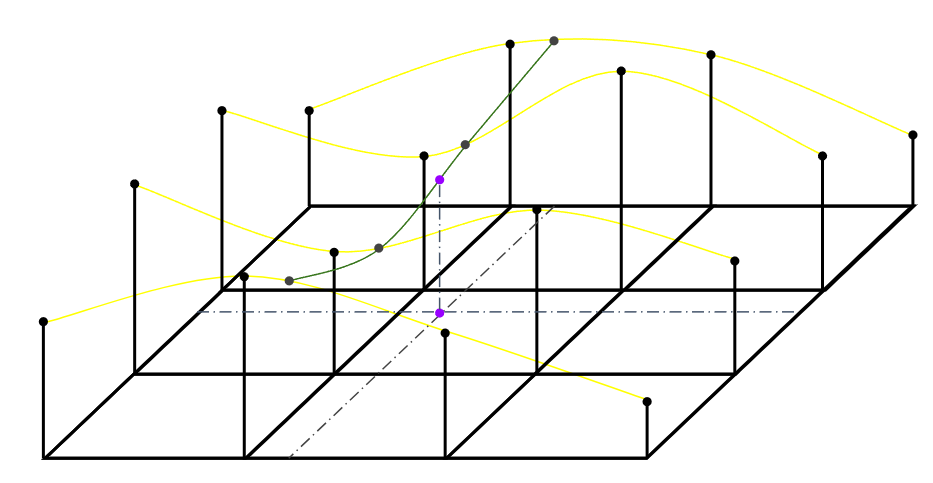
앞서 구한 4개의 점을 이용하여 한번 더 보간을 진행해 값을 구해준다.