기술통계(Descriptive Statistics)와 추론 통계(Inferential Statistics)는 통계학의 두 가지 주요 분야이다. 이 두 분야는 데이터 분석과 해석을 위해 사용되며 각자의 목적과 방법이 다르다.

1. 기술통계

• 기술통계는 데이터를 요약하고 설명하는데 사용된다.
• 기술통계는 데이터의 특성을 이해하고 데이터의 중심 경향, 분산, 분포, 형태 등을 파악하는데 도움을 준다.

📖 방법

1) 평균

평균(Mean)은 데이터 집합의 중심 경향을 나타내는 통계적 측도이다. 평균은 데이터의 모든 값을 더한 후 데이터의 개수로 나누어 계산된다. -> 평균 = (데이터의 합) / (데이터의 개수) 평균은 데이터 집합의 대표값 중 하나로, 데이터의 중심 위치를 알려준다.

평균은 연속형 데이터와 이산형 데이터 모두에 적용할 수 있으며, 데이터의 중심 경향을 이해하고 비교하는 데 유용하다.

🔎 코드 예제

# 필요한 모듈 불러오기
import numpy as np

# 데이터 집합 생성
data = [12, 15, 18, 22, 25]

# 데이터의 평균 계산
mean = np.mean(data)

# 결과 출력
print("데이터 집합:", data)
print("평균:", mean)

위 코드에서는 NumPy 모듈을 사용하여 데이터 집합의 평균을 계산한다. mean()이라는 함수를 사용해 data의 평균을 구할 수 있다.

2) 중앙값

중앙값(Median)은 데이터 집합을 정렬했을 때 중간에 위치하는 값이다. 중앙값은 데이터를 중심으로 나눌 때 사용되며, 이상치(극단적으로 크거나 작은 값)에 덜 민감한 통계적 측도이다. 중앙값은 말 그대로 중앙에 위치한 값으로, 데이터의 분포에서 중심 위치를 나타내는 대표값 중 하나이다.

중앙값을 찾는 방법은 다음과 같다.

데이터를 오름차순으로 정렬한다.
데이터의 개수가 홀수인 경우: 중간에 위치한 값을 중앙값으로 선택한다.
데이터의 개수가 짝수인 경우: 중간에 위치한 두 값을 더한 후 2로 나눈 값을 중앙값으로 선택한다.

🔎 코드 예제

import numpy as np

# 데이터 집합 생성
data = np.array([12, 15, 18, 22, 25, 30])

# 중앙값 계산
median = np.median(data)

# 결과 출력
print("중앙값:", median)

위 코드에서는 NumPy 모듈를 사용하여 데이터 집합의 중앙값을 계산한다. median()이라는 함수를 사용해 data의 중앙값을 구할 수 있다.

3) 최빈값

최빈값은 주어진 데이터 집합 내에서 가장 빈번하게 나타나는 값입니다. 최빈값은 데이터의 분포를 이해하고 데이터가 어떻게 분포되어 있는지 파악하는데 사용된다.

🔎 코드 예제
- statistics 모듈 이용

from statistics import mode

# 데이터 집합 생성
data = [12, 15, 18, 18, 22, 25, 30, 30, 30]

# 최빈값 계산
mode_value = mode(data)

# 결과 출력
print("최빈값:", mode_value)

위 코드에서 statistics 모듈의 mode() 함수를 사용하여 최빈값을 계산한다. 데이터 집합은 리스트로 생성되며, mode(data)를 호출하여 최빈값을 찾는다.

- SciPy 모듈 이용

import numpy as np
from scipy import stats

# 데이터 집합 생성
data = np.array([12, 15, 18, 18, 22, 25, 30, 30, 30])

# 최빈값 계산
mode_value = stats.mode(data)

# 결과 출력
print("데이터 집합:", data)
print("최빈값:", mode_value.mode)

위 코드에서는 NumPy 배열을 사용하여 데이터 집합을 생성하고, SciPy의 stats.mode() 함수를 사용하여 최빈값을 계산합니다.

4) 분산

분산(Variance)은 데이터 집합의 분포나 데이터 포인트 간의 퍼짐 정도를 나타내는 통계적 측도이다. 분산은 데이터 포인트와 평균값 간의 차이(편차)를 제곱한 값의 평균으로 계산된다. 다시말해, 편차의 합의 제곱의 평균이라고 할 수 있다. 높은 분산은 데이터가 평균에서 멀리 퍼져있음을 나타내며, 낮은 분산은 데이터가 평균 주변에 모여 있음을 나타낸다.

- 분산 수식

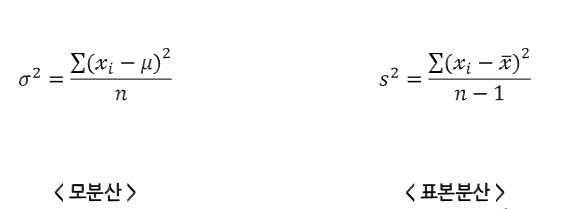
xi는 데이터 포인트, 뮤 또는 x바는 평균, n은 집합의 개수를 듯한다. 모분산과 표본분산의 차이는 나중에 다루도록 하겠다.

🔎 코드 예제

import numpy as np

# 데이터 집합 생성
data = [12, 15, 18, 22, 25, 30]

# 분산 계산
variance = np.var(data)

# 결과 출력
print("분산:", variance)

위 코드에서는 NumPy를 사용하여 데이터 집합을 생성하고, np.var(data)를 사용하여 데이터의 분산을 계산한다.

5) 표준편차

표본편차(Sample Standard Deviation)는 데이터 집합의 퍼진 정도를 나타내는 통계적 측도 중 하나이다. 표본편차는 데이터 포인트와 표본의 평균 간의 차이를 나타내며, 데이터의 분산(분포도)를 측정하는 중요한 값 중 하나이다.

• 수식
  
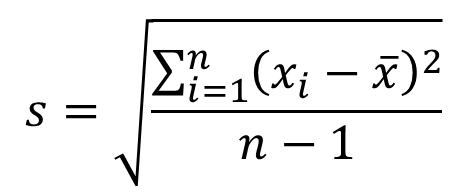
  간단하게 분산에 루트를 씌운 것이 표준편차라고 생각하면 된다.

🔎 코드 예제

import numpy as np

# 데이터 집합 생성
data = [12, 15, 18, 22, 25, 30]

# 데이터의 표본편차 계산
sample_std_dev = np.std(data, ddof=1)  # ddof=1은 자유도(표본 크기 - 1)를 고려하는 옵션

# 결과 출력
print("표본편차:", sample_std_dev)

위 코드에서는 NumPy를 사용하여 데이터 집합을 생성하고, np.std(data, ddof=1)를 사용하여 데이터의 표본편차를 계산한다. ddof=1은 표본의 자유도를 고려하는 옵션이다.

6) 백분위수

백분위수(Percentile)는 데이터 집합 내에서 특정 백분율 위치에 있는 값을 나타내는 통계적 측도이다. 백분위수는 데이터를 정렬하고 해당 백분율 위치에 있는 값이 어떤 값인지를 나타내며 데이터의 분포를 이해하는데 도움을 준다. 일반적으로 전체를 4등분한 4분위수를 많이 사용한다.

4분위수란?

제 1 사분위 수 = Q1 = 제 25 백분위수
제 2 사분위 수 = Q2 = 제 50 백분위수
제 3 사분위 수 = Q3 = 제 75 백분위수

4분위수 범위(IQR, interquartile)란?

제 3 사분위와 제 1 사분위 사의 거리다. 자료의 퍼진 정도의 측도로 사용할 수 있다.
사분위수 범위 : IQR = 제 3 사분위수 - 제 1 사분위수 = Q3 - Q1
IQR은 상위 25%의 관측값과 하위 25%의 관측값을 제외한 중앙에 위치함 50%의 관측값의 퍼진 정도를 나타낸다. 따라서, 극단값에 영향을 받지 않는다.

🔎 코드 예제

import numpy as np

# 데이터 집합 생성
data = [12, 15, 18, 22, 25, 30, 35, 40, 45, 50]

# 1사분위 (Q1) 계산
q1 = np.percentile(data, 25)

# 2사분위 (중앙값, Median) 계산
median = np.percentile(data, 50)

# 3사분위 (Q3) 계산
q3 = np.percentile(data, 75)

# 결과 출력
print("1사분위 (Q1):", q1)
print("2사분위 (중앙값):", median)
print("3사분위 (Q3):", q3)

위 코드에서는 NumPy를 사용하여 데이터 집합을 생성하고, np.percentile(data, 백분위) 함수를 사용하여 각 사분위수를 계산한다.

7) 히스토그램

히스토그램은 데이터 분포를 시각화하는 데 사용되는 그래픽 도구로, 데이터의 빈도를 막대 그래프로 표현하는 방법이다. 다음은 히스토그램의 주요 개념과 특징에 대한 설명이다.

1. 데이터 분포 표현

히스토그램은 데이터 집합의 값을 구간(빈)으로 나누고, 각 구간에 속하는 데이터 포인트의 빈도를 시각적으로 나타낸다. 이를 통해 데이터의 분포와 특성을 파악할 수 있다.

2. 데이터 빈도

히스토그램의 막대 그래프는 각 데이터 구간에 속하는 데이터 포인트의 수 또는 상대적 비율을 나타낸다. 이것은 데이터가 특정 구간에 집중되어 있는지, 어떤 구간에서 빈도가 높은지를 시각화로 확인하는 데 도움이 된다.

3. 계급 또는 구간 설정

데이터의 범위를 일정한 길이 또는 크기의 구간(빈)으로 나누어야 한다. 이러한 구간의 폭을 설정함으로써 히스토그램의 모양이나 해석이 달라질 수 있다. 일반적으로 구간의 수 또는 폭은 사용자가 설정하며, 적절한 값은 데이터의 특성에 따라 다를 수 있다.

4. 가로축과 세로축

히스토그램의 가로축은 데이터 값의 범위 또는 구간을 나타내며, 세로축은 해당 구간에 속하는 데이터의 빈도를 나타낸다. 따라서 가로축은 데이터의 연속적인 범위 또는 이산적인 값에 해당하고, 세로축은 해당 범위의 데이터가 얼마나 빈번하게 발생하는지를 나타낸다.

5. 데이터 분포 특징 확인

히스토그램을 통해 데이터의 중심 경향(평균, 중앙값), 분산, 왜도(데이터의 비대칭 정도), 첨도(데이터의 뾰족함 정도) 등을 시각적으로 확인할 수 있다. 또한, 이상치나 이상한 패턴도 히스토그램을 통해 식별할 수 있다.

6. 데이터 전처리와 분석 도구

히스토그램은 데이터 탐색, 전처리 및 분석 과정에서 유용하게 활용된다. 데이터의 분포를 이해하고, 데이터의 특성을 발견하고, 적절한 분석 방법을 선택하기 위한 기본 단계로 활용된다.

🔎 코드 예제

import matplotlib.pyplot as plt
import numpy as np

data = np.random.randn(1000)  # 난수 데이터 생성

# 히스토그램 그리기
plt.hist(data, bins=30, color='blue', alpha=0.7)
plt.title('간단한 히스토그램')
plt.xlabel('데이터 값')
plt.ylabel('빈도')
plt.grid(True)
plt.show()

이 코드에서는 numpy와 matplotlib를 사용하였다. numpy는 데이터 생성을 위해 사용되고, matplotlib를 사용해서 히스토그램을 그렸다.
plt.hist() 함수를 사용하여 히스토그램을 생성하고, 히스토그램의 막대의 수(bins)는 30개로 설정되었다. color는 막대의 색상을 나타내며, alpha는 투명도를 나타낸다. plt.title(), plt.xlabel(), plt.ylabel() 함수를 사용하여 제목과 축 레이블을 설정하였고, plt.grid(True)를 사용하여 그리드를 표시하였다. 마지막으로, plt.show() 함수를 호출하여 그래프를 표시한다.

8) 상자 그림

상자그림(box plot 또는 box-and-whisker plot)은 데이터의 분포를 시각화하는 방법 중 하나로, 주로 데이터의 중앙 경향, 분산, 이상치를 표시한다. 상자그림은 주로 다수의 데이터 그룹 또는 변수를 비교할 때 사용되며, 각 그룹의 중앙 경향, 분산 및 이상치 여부를 빠르게 시각화하여 비교할 수 있다. 이를 통해 데이터 분포의 특성을 파악하고 데이터 집단 간 비교를 수행하는 데 도움이 된다. 상자그림은 통계 분석, 연구, 데이터 시각화 등 다양한 분야에서 유용하게 활용된다.
상자그림의 주요 개념은 다음과 같다.

1. 중앙 경향(중앙값, 중앙값, 2사분위수)

상자그림의 중앙 부분에 위치한 수평선은 데이터의 중앙 경향을 나타낸다. 이 수평선은 데이터를 정렬했을 때 중앙에 있는 값, 즉 중앙값(median)이다. 중앙값은 데이터의 중심을 나타낸다.

2. 상자(Interquartile Range, IQR)

상자그림의 상자는 데이터의 중간 50% 범위를 표현합니다. 앞에서 설명한 4분위수 범위(IQR)를 말하는 것이다. IQR은 데이터의 분산을 나타내며 데이터의 중심 경향을 중앙값 대신 사용할 때 이상치를 감지하는데 유용하게 사용된다.

3. 수염(Whiskers)

상자 위와 아래에 그려진 선을 수염이라고 합니다. 수염은 데이터의 범위를 나타내며, 일반적으로 Q1에서 1.5 IQR 떨어진 최소값과 Q3에서 1.5 IQR 떨어진 최대값까지 그려진다. 이 범위를 벗어나는 데이터 포인트는 이상치로 간주된다.

4. 이상치(Outliers)

상자그림에서 수염 밖에 있는 개별 데이터 포인트들을 이상치로 간주한다. 이상치는 주로 수염을 벗어난 극단적인 값으로, 데이터 분포의 극단적인 특성을 나타낸다.

🔎 코드 예제

import seaborn as sns
import matplotlib.pyplot as plt

data = [62, 68, 72, 77, 80, 82, 85, 88, 90, 100]

# 상자그림 그리기
sns.set(style="whitegrid")  # 그리드 스타일 설정 (선택사항)

plt.figure(figsize=(6, 4))  # 그래프 크기 설정 (선택사항)
sns.boxplot(x=data, color='lightblue')

plt.title("상자그림 예제")
plt.xlabel("데이터")
plt.show()

상자그림(Box Plot)을 그리기 위해 파이썬의 matplotlib 또는 seaborn 라이브러리를 사용할 수 있다. 위 코드는 seaborn 라이브러리를 활용한 상자그림 코드 예제이다.
sns.boxplot() 함수를 사용하여 상자그림을 그리고, 그래프의 제목과 축 레이블을 설정한다. plt.show() 함수를 호출하여 그래프를 표시한다.

이 외에도 다른 방법들이 존재한다.

2. 추론 통계

• 추론 통계는 표본 데이터를 사용하여 모집단에 대한 결론을 유추하거나 예측하는데 사용된다.
• 추론 통계는 불확실성과 오류를 고려하여 통계적 추론을 수행한다.
• 가설 검정, 신뢰구간, 회귀 분석, 분산 분석, 표본 추출, 확률 분포, 통계적 검정 등이 있다.
  가설 검정, 신뢰 구간 등의 포스팅은 하나씩 자세하게 다음 포스팅부터 올릴 예정이다.
  
  
  

요약하면, 기술통계는 데이터의 특성을 요약하고 설명하는데 사용되며, 데이터의 특징을 파악하는 데 중점을 둔다. 반면에 추론 통계는 표본 데이터를 사용하여 모집단에 대한 결론을 도출하고 예측하는데 사용되며, 불확실성과 통계적 추론에 관심을 둔다. 이 두 분야는 데이터 분석의 다른 측면을 다루며, 데이터 과학, 경제학, 생물학, 사회과학 등 다양한 분야에서 활용됩니다.

수식 이미지 출처 : https://www.mfgkr.com/archives/17158

백분위수 참고 : https://leedakyeong.tistory.com/entry/%EA%B8%B0%EC%B4%88%ED%86%B5%EA%B3%84-%EB%B0%B1%EB%B6%84%EC%9C%84%EC%88%98%EC%99%80-%EC%82%AC%EB%B6%84%EC%9C%84%EC%88%98-What-is-Percentile-and-Interquartile-Range

상자수염 그림 출처 : https://hsm-edu.tistory.com/1542