저번 포스팅 에서 머신러닝에 대해서 공부해 보았다. 회귀 분석은 머신러닝(지도학습)에 포함되는 개념이라고 볼 수 있다.
회귀분석에는 선형 회귀, 로지스틱 회귀, 다항 회귀, 릿지& 라쏘 회귀, ElasticNet 회귀, 시계열회귀, 베이지안 회귀 등이 있다. 요번 포스팅에서는 선형 회귀에 대해 알아보려고 한다.

📕 개념

선형 회귀 분석이란? 관찰된 데이터를 기반으로 두 변수 간의 관계를 모델링하는 통계적 기법 중 하나이다. 이는 종속 변수(예측하고자 하는 변수)와 하나 이상의 독립 변수(예측에 사용되는 변수) 간의 선형 관계를 설명하고 예측하는 데 사용된다.

📍 주요 개념

1. 선형 관계

• 선형 회귀는 독립 변수와 종속 변수 간의 관계를 직선 형태로 모델링하는 것이다.
• 단일 선형 회귀는 하나의 독립 변수로 종속 변수를 예측하는 반면, 다중 선형 회귀는 여러 독립 변수로 종속 변수를 예측한다.
  
  
  2. 회귀식
• 모델을 표현하는 방정식으로, 일반적으로 독립 변수들과 그에 상응하는 계수들로 표현된다.
• 단순 선형 회귀의 경우, 식은 y = ax + b 형태이다.
  - 중학교 때 배웠던 직선의 방적이다. a는 절편, b는 기울기이다.
• 다중 선형 회귀의 경우, 식은 y = b0 + b1x1 + b2x2 + ... + bn*xn 형태이다.
• 가장 합리적인 추세선이란? 오차의 제곱이 최소화되는 추세선이다.
  
  
  3. 최소제곱법
  최소제곱법(Least Squares Method)은 회귀 분석에서 사용되는 주요 기법 중 하나이다. 최소제곱법은 추세선을 구하기 위해 사용되는 방법이라고 할 수 있다. 회귀선(또는 모델)을 생성할 때 실제 데이터와 모델로 예측한 값 사이의 잔차(오차)의 제곱을 최소화하여 최적의 모델을 찾는 것을 목표로 한다.
  이 방법을 영어로 OLS(Ordinary Least Square)라고도 한다.

💡 최소제곱법 살펴보기

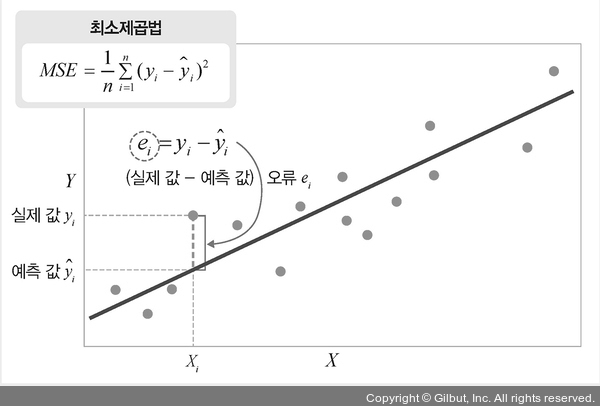
1. 오차항 (Error Term)

• 개념: 모델링하는 과정에서 관찰되지 않는 현상을 나타내는 부분으로, 회귀 분석에서 종속 변수와 독립 변수 간의 관계를 설명하지 못하는 부분을 말한다.
• 특징: 이론적으로 우리는 오차항의 실제 값을 알 수 없다. 오차항은 종속 변수와 독립 변수 사이의 복잡한 관계나 외부 요인 등을 나타내며, 실제 관측하지 못하는 부분이다.

2. 잔차 (Residuals)

• 개념: 실제 관측값과 모델로 예측된 값 사이의 차이를 말합니다. => 실제 값 - 예측 값
• 특징: 모델을 통해 얻은 잔차는 실제로 계산되고 모델의 성능 평가에 사용된다.

2-2. 오차항과 잔차의 차이점

• 기원: 오차항은 모델링할 때 고려되지 않는 관측되지 않는 요인을 의미하며, 이는 모델의 복잡성을 나타낸다. 반면에 잔차는 실제 관측값과 모델로 예측한 값 간의 차이를 나타내며, 모델의 예측력과 성능을 측정하는 데 사용된다.
• 계산: 오차항은 실제 값과 모델 사이의 차이로 계산되지 않으며, 잔차는 회귀 모델을 통해 계산된다.
• 활용: 잔차는 모델의 적합성을 평가하거나 모델의 수정에 사용되는 반면, 오차항은 통계적 모델링의 잠재적인 부분을 설명하는 데 사용된다.

3. 최소제곱법 원리

• 최소제곱법은 잔차 제곱의 합을 최소화하는 회귀선(또는 모델)을 찾는 방법이다.
• 각 데이터 포인트에서 예측값과 실제 값 간의 차이(잔차)를 제곱하여 모든 데이터 포인트의 잔차를 합산한 후, 이 값이 최소가 되도록 회귀선을 조정한다.
• 일반적으로 회귀선은 예측값과 실제 값의 차이(잔차)를 나타내는 제곱 오차의 합을 최소화하는 방향으로 결정된다. 이를 최적화라고 할 수 있다.

📍 가정

선형 회귀 분석은 몇 가지 가정에 기반하여 데이터에 대한 모델링을 시도한다. 이러한 가정들이 만족되어야 회귀 분석 결과가 신뢰할 만한 것으로 간주된다.

1. 선형성

• 종속 변수와 독립 변수 간의 관계가 선형적이어야 한다. 즉, 독립변수(feature)의 변화에 따라 종속변수도 일정 크기로 변화해야 한다.
• 회귀식이 직선이 아닌 곡선이거나 다항식으로 표현되는 경우에는 데이터를 변환하거나 다른 모델을 사용해야 할 수 있다.

2. 정규성

• 오차 항은 정규 분포를 따라야 한다. 즉, 오차들이 평균을 중심으로 대칭적으로 분포되어야 힌다.
• 오차 항이 정규성 가정을 만족하지 않으면 통계적 검정 및 신뢰 구간 추정 등에서 문제가 발생할 수 있다.

3. 독립성

• 독립변수의 값이 서로 관련되지 않아야 한다.

4. 등분산성

• 등분산성이란? 모집단과 표본집단의 통계량들이 동일한 분산을 갖는 성질이다.
• 그룹간의 분산이 유사해야 한다. 독립변수의 모든 값에 대한 오차들의 분산은 일정해야 한다.
• 등분산성이 없는 경우에는 산포가 일정하지 않아 모델의 예측력이 낮아질 수 있다.

5. 다중공선성

• 회귀 분석에서 독립 변수들 간에 높은 상관 관계가 있는 상황을 가리킨다.
• 다중회귀 분석 시 두 개 이상의 독립변수 간에 강한 상관관계가 있어서는 안된다.
  
  
  

📍 유형

1. 단순 선형 회귀 (Simple Linear Regression)

• 한 개의 독립 변수(X)와 한 개의 종속 변수(Y) 간의 관계를 설명하는 모델이다.

2. 다중 선형 회귀 (Multiple Linear Regression)

• 둘 이상의 독립 변수(X1, X2, X3, ...)와 한 개의 종속 변수(Y) 간의 관계를 설명하는 모델이다.

차이점

• 독립 변수의 수: 단순 선형 회귀는 하나의 독립 변수를 사용하고, 다중 선형 회귀는 둘 이상의 독립 변수를 사용합니다.
• 모델의 복잡성: 다중 선형 회귀는 더 많은 독립 변수를 고려하기 때문에 모델의 복잡성이 단순 선형 회귀보다 높을 수 있습니다.
• 변수 간 관계: 단순 선형 회귀는 한 개의 독립 변수와 종속 변수 간의 직선적인 관계를 모델링하며, 다중 선형 회귀는 여러 독립 변수 간의 복잡한 관계를 모델링할 수 있습니다.

단순 선형 회귀는 개념을 이해하기 쉽고 해석하기 쉽지만, 현실 세계의 많은 경우에는 다중 선형 회귀를 사용하여 복잡한 관계를 더 잘 설명할 수 있다.

📕 실습

선형 회귀 분석을 지원하는 python 라이브러리는 많지만, 나는 이중 두가지에 대해 설명하고 예시 코드를 리뷰하려고 한다.

📍 statsmodels의 ols

ols는 statsmodels 라이브러리에 있는 방법이다. ols는 선형 회귀의 기초를 형성하며, 회귀 분석에서 주로 사용되는 방법중 하나이다. ols를 사용하면 통계적인 요소들(계수의 유의성, 모델의 적합성 등)을 포함한 선형 회귀 분석 결과를 쉽게 얻을 수 있다. ols는 주어진 데이터에 대한 선형 회귀 모델을 적합시키는 방법 중 하나로, 가장 일반적으로 사용되며 직관적으로 이해하기 쉽다.

🔎 코드 예시

import numpy as np
import statsmodels.api as sm

# 예제 데이터 생성
np.random.seed(0)
X = np.random.rand(100, 1)  # 독립 변수
y = 2 * X.squeeze() + np.random.normal(size=100)  # 종속 변수

# 상수항 추가
X = sm.add_constant(X)

# OLS 모델 생성 및 피팅
model = sm.OLS(y, X).fit()

# 모델 요약 정보 출력
print(model.summary())

🔎 코드 리뷰

1. numpy를 사용하여 랜덤한 독립 변수 X와 그에 해당하는 종속 변수 y를 생성한다.
2. add_constant 함수를 사용하여 독립 변수에 상수항(절편)을 추가힌다.
3. statsmodels의 OLS 함수를 사용하여 X와 y를 이용해 OLS 모델을 생성한다.
4. fit 함수를 사용하여 모델을 피팅(적합)한다.
5. summary 메서드를 사용하여 모델 요약 정보를 출력한다.

이 코드를 실행하면, OLS에 의해 추정된 회귀 모델의 요약 정보(summary)가 출력된다. 이 정보에는 모델의 R-squared(결정 계수), 회귀 계수(coefficient), p-value 등이 포함된다. 이를 통해 모델의 적합성과 변수들 간의 관계에 대한 정보를 확인할 수 있다.
(이에 대한 자세한 설명은 다음 포스팅에서 하도록 하겠다.) -> ols summary 자세히 보기

📍 scikit-learn

scikit-learn은 머신러닝을 위한 가장 널리 사용되는 라이브러리 중 하나이다. 선형 회귀뿐만 아니라 다양한 머신러닝 모델을 제공한다. sklearn.linear_model.LinearRegression은 선형 회귀를 수행하는 클래스입니다. 이외에도 Ridge, Lasso 등의 변형된 회귀 모델도 지원한다.

ols와 명확하게 다른 점 하나는 cikit-learn은 summary를 제공하지 않는다는 점이다.

🔎 코드 예시

from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt

# 데이터 생성 (가상 데이터)
X, y = make_regression(n_samples=100, n_features=1, noise=10, random_state=42)

# 데이터 분할 (학습용 데이터와 테스트용 데이터)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 선형 회귀 모델 생성 및 학습
model = LinearRegression()
model.fit(X_train, y_train)

# 테스트 데이터로 예측
y_pred = model.predict(X_test)

# 성능 측정 (MSE 및 R-squared)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

# 결과 출력
print(f"Mean Squared Error (MSE): {mse}")
print(f"R-squared (R2): {r2}")

# 시각화
plt.scatter(X_test, y_test, color='black')
plt.plot(X_test, y_pred, color='blue', linewidth=3)
plt.show()

🔎 코드 리뷰

1. make_regression 함수를 사용하여 가상의 회귀용 데이터를 생성한다.
2. train_test_split 함수로 데이터를 학습용과 테스트용으로 분할한다. 여기선 train 80%, test 20%의 비율로 분할하였다.
3. LinearRegression 클래스를 사용하여 선형 회귀 모델을 생성하고, fit 메서드로 학습 데이터에 모델을 적합시킨다.
4. 학습된 모델을 사용하여 테스트 데이터로 예측을 수행하고, mean_squared_error 및 r2_score를 통해 모델의 성능을 측정한다.
5. matplotlib 라이브러리를 활용하여 시각화를 통해 실제 데이터와 예측된 회귀선을 비교한다.
   
   
   

📍 기본 가정 충족 여부 확인

기본 가정은 위에서 설명한 가정 다섯 가지인 선형성, 정규성, 독립성 , 등분산성 , 다중공선성을 말한다.

🔎 코드 예시

회귀 분석의 기본 가정을 확인하기 위해 일반적으로 다양한 방법과 통계적 도구를 사용합니다. 여기에는 회귀 모델의 적합성을 검증하고 가정을 충족하는지 확인하는 다양한 방법이 있습니다. 아래의 코드는 Python을 사용하여 회귀 모델의 기본 가정을 확인하는 방법을 보여줍니다.

import statsmodels.api as sm
import numpy as np
import matplotlib.pyplot as plt

# 임의의 데이터 생성
np.random.seed(0)
X = np.random.rand(100, 1)  # 독립 변수
y = 2 * X.squeeze() + np.random.randn(100)  # 종속 변수 (잡음 추가)

# 선형 회귀 모델 적합
X_with_const = sm.add_constant(X)  # 절편 추가
model = sm.OLS(y, X_with_const).fit()

# 기본 가정 확인
# 1. 선형성 확인
plt.scatter(X, y)
plt.plot(X, model.predict(X_with_const), color='red')  # 적합된 선형 모델 그래프
plt.title('선형성 확인')
plt.xlabel('독립 변수')
plt.ylabel('종속 변수')
plt.show()

# 2. 정규성 확인 (잔차의 정규성 확인)
residuals = model.resid
sm.qqplot(residuals, line='s')
plt.title('잔차의 정규성 확인')
plt.show()

# 3. 독립성 확인 (잔차의 자기상관 확인)
sm.graphics.tsa.plot_acf(residuals, lags=30)
plt.title('잔차의 자기상관 확인')
plt.show()

# 4. 등분산성 확인 (잔차의 등분산성 확인)
plt.scatter(model.fittedvalues, residuals)
plt.xlabel('적합된 값')
plt.ylabel('잔차')
plt.title('잔차의 등분산성 확인')
plt.show()

# 5. 다중공선성 확인 (VIF를 통한 다중공선성 확인)
from statsmodels.stats.outliers_influence import variance_inflation_factor
vif = [variance_inflation_factor(X_with_const.values, i) for i in range(X_with_const.shape[1])]
print('다중공선성 (VIF):', vif)

🔎 코드 리뷰

1. 데이터 생성: 임의의 데이터 생성 (독립 변수 X와 종속 변수 y)하여 분석용 데이터 생성.
2. 회귀 모델 적합: statsmodels를 사용하여 OLS(Ordinary Least Squares)를 통해 선형 회귀 모델을 적합.
3. 기본 가정 확인:
   • 선형성 확인: 산점도 및 회귀 모델의 적합 그래프를 시각화하여 확인.
   • 정규성 확인: 잔차의 정규성을 QQ 플롯으로 시각화하여 확인.
   • 독립성 확인: 잔차의 자기상관을 ACF(AutoCorrelation Function) 그래프로 확인.
   • 등분산성 확인: 적합된 값과 잔차의 산포도를 통해 등분산성 확인.
   • 다중공선성 확인: VIF(Variance Inflation Factor)를 통해 다중공선성 확인.

최소제곱법 이미지 : https://thebook.io/080289/0117/