Linear regression ;선형회귀
1. Hypothesis
2. Cost function
3. Gradient descent
Multivariable Linear regression
1. Hypothesis
2. Cost function
Linear regression
연속적인 숫자를 예측하는 task
입력값과 정답값을 통해 선을 그려서 새로운 입력값이 나오면 그 선으로 부터 새로운 입력에 대한 정답을 유추함
Hypothesis (가설 설정)
H(x) = Wx + b (Linear Hypothesis) -> 1차 방정식
함수의 답과 실제 정답의 차이가 적은 Hypothesis(가설)이 좋은 가설임
W와 b가 모델의 파라미터
Cost function (손실 함수)
cost function = Loss function = Objective function
cost(W,b) = H(x) - y (Predict - GT)
함수의 답과 실제 정답의 차이를 의미하며 앞서 얘기한것 처럼 cost가 작으면 작을 수록 좋은 가설이며 cost는 작을 수록 좋음
cost =
전체 Sample의 평균 cost를 구함
목표
결국 가장 작은 cost값을 갖게 하는 W와b를 찾는것이 선형회귀의 솔루션을 구하는 방법
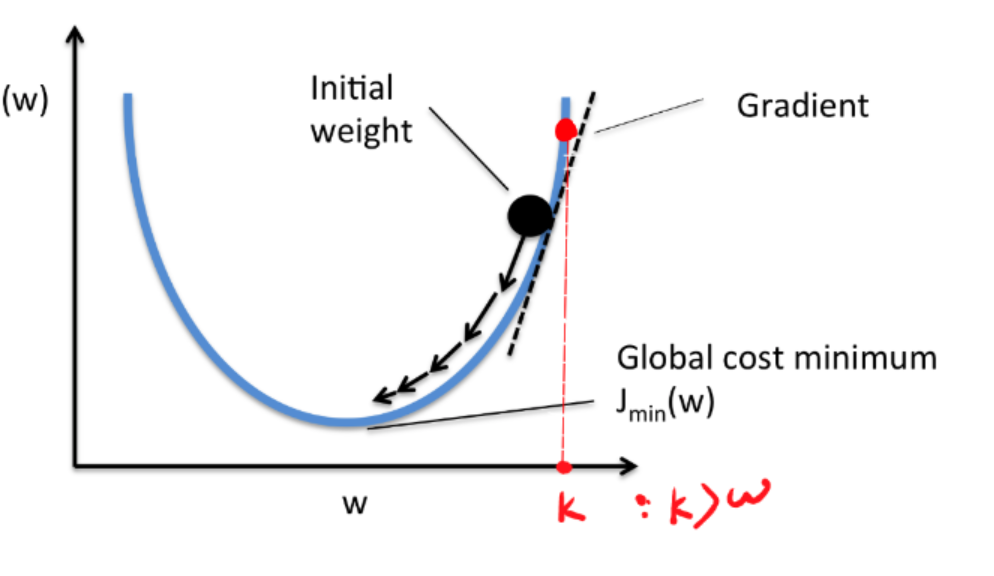
Gradient descent algorithms (경사 하강 알고리즘)
> minimize cost function
> Gradient descent is used many minimization problems
> For a given cost function cost(W,b), it will find W, b to minimize cost
> It can be applied to more general function: cost(w1, w2, ...)
< Linear regression cost function graph >
cost function의 수식에서 (Wx+b - y)만 봤을 때 x와 y는 상수일 때 형태를 갖기 때문에 2차 그래프가 그려짐
> 기울기가 0이 될 때 까지 값을 조정함
기울기가 0이 될 때 까지 를 조정하지만 가 더 이상 변하지 않는 cost를 구함
즉, 값이 더 이상 변하지 않을 때 까지 Gradient descent Algorithm을 반복
기울기는 미분을 통해서 구할 수 있음
<Foramal definition of "Gradient Descent Algorithm">
: 기울기
*보통 는 0.1이나 0.01과 같은 값