통계가 중요한 이유?
통계로 데이터를 이해하고 해석할 수 있다.
데이터를 요약하고 패턴을 발견할 수 있다.
추론을 통해 결론을 도출화하는 과정을 돕는다.
= 데이터 기반의 의사결정!
1) 기술 통계
- 데이터를 요약하고 설명하는 통계 방법 (평균,중앙값,분산,표준편차 등)
- 데이터를 특정 대표값으로 요약
평균 : 데이터의 중앙값 (모든 데이터를 더한 후 데이터 개수로 나누기
= 데이터의 일반적인 경향을 파악하는데 유용
중앙값 : 데이터를 크기 순으로 정렬할 때 중앙에 위치한 값.
= 이상치의 영향을 덜 받기 때문에 데이터의 중심 경향을 나타내는 또 다른 방법
EX) 20대 평균 소득이 5,000만원이다? => 뉴진스라는 이상치의 영향
분산 : 데이터의 값이 평균으로부터 얼마나 떨어져 있는지를 나타냄. 데이터의 흩어짐 정도.
= 분산이 크면 데이터가 넓게, 작으면 평균에 가깝게 모여있음을 의미
- 각 데이터 값에서 평균을 뺀 값을 제곱한 후 모두 더하고 데이터의 개수로 나누어서 구함.
표준편차 : 데이터 값들이 평균에서 얼마나 떨어져있는지를 나타내는 통계적 척도, 분산의 제곱근으로 계산
= 데이터의 변동성을 측정하며, 값이 클수록 평균으로부터 넓게 퍼져있음
2) 추론 통계
- 표본 데이터를 통해 모집단의 특성을 추정하고 가설을 검정하는 통계 방법
- 데이터의 일부를 가지고 전체를 추정
- 신뢰구간, 가설검정 등을 사용
신뢰구간 : 모집단의 평균이 특정 범위 내에 있을 것이라는 확률
- 일반적으로 95%의 신뢰구간이 사용
- 만약 평균 만족도가 75점이고 신뢰구간이 70점에서 80점이라면 95%확률로 실제 평균 만족도가 범위 내에 있다고 말할 수 있음.
가설검정 : 모집단에 대한 가설을 검증하기 위해 사용
1. 귀무가설 : 검증하고자하는 가설이 틀렸음을 나타내는 기본가설.
2. 대립가설 : 반대가설로 주장하는 바를 나타냄.
= p-value를 통해 귀무가설을 기각할지 여부 결정
EX) 새로운 교육프로그램이 학생들의 성적에 영향을 미치는가?
-> 귀무가설 : 프로그램이 성적에 영향을 미치지 않는다.
-> 대립가설 : 프로그램이 성적에 영향을 미친다.
통계의 분석 방법
1) 위치추정
데이터의 중심을 확인하는 방법 = 평균, 중앙값 확인
- 평균 및 중앙값을 파이썬에서 구하는 법
EX)
data= [85,90,78 ...]
mean = np.mean(data) > 평균
median = np.median(data) > 중앙값
numpy = 쉽게 계산을 하도록 돕는 라이브러리
2) 변이추정
데이터들이 서로 얼마나 다른지 확인하는 방법 = 분산, 표준편차, 범위 등 사용
범위 : 데이터에서 가장 큰 값과 가장 작은 값의 차이.
- 변동성을 확인할 때 사용
분산 = np.var()
표준편차 = np.std()
범위 = np.max() - np.min()
3) 데이터 분포 탐색
데이터의 값들이 어떻게 이루어져 있는지 확인하기 = 하나의 대표값이 아닌 여러 값이 나오며, 히스토그램과 상자그림으로 시각적으로 표현
- 히스토그램 : 데이터를 구간별로 나누어 각 구간에 몇 개의 데이터가 있는지 막대그래프 형태로 표현
plt.hist(data, bins=5) - 박스 그림 : 상위 25%~하위25%의 값들을 박스 안에 넣음
plt.boxplot(data)
4) 이전 데이터와 범주 데이터 탐색
데이터들이 서로 얼마나 다른지 확인하는 방법 = 최빈값을 주로 사용, 파이그림과 막대그래프가 대표적인 시각화
통계학 세션
데이터의 종류
1. 수치형 데이터 : 숫자를 이용해 표현할 수 있는 데이터
1-1) 연속형 : 일정 범위 안에서 어떤 값이든 취할 수 있는 데이터 (체중,신장)
1-2) 이산형 : 횟수와 같은 정수형 값만 취할 수 있음 (소수점 X)
- 범주형 데이터 : 범주(카테고리) 안의 값만 취하는 데이터 (성별, 나라, 도시 등)
2-1) 이진형 : 두 개의 값만을 가지는 범주형 데이터의 특수 경우 (성별, 성공여부)
2-2) 순서형 : 값들 사이에 순위가 있는 데이터 (등수)
편차, 분산, 표준편차, 표본분포..?
편차 : 각 점수가 평균에서 얼마나 떨어져 있는지를 계산한 값 (점수 - 평균)
다만! 전체의 편차를 나타내기 위해 각각의 편차를 모두 더하면 0이 됨.
따라서~ 편차로는 반 전체의 점수 분포를 알 수 없기에 분산을 활용
분산 : 편차의 합이 0으로 나오는 것을 방지하기위한 개념 (편차를 제곱해서 평균 낸 값)
다만 ! 제곱을 해줬기에 값이 너무 크게 나옴.
따라서~ 이를 해결하기 위해 표준편차를 활용
표준편차 : 분산의 제곱근, 분산은 단위가 제곱이라 해석이 어렵기에 표준편차로 원래 단위로 다시 바꿔줌.
EX) 분산이 466이면 분산의 제곱근인 표준편차는 약 21.6
= 따라서 전체의 점수가 약 21.6만큼 퍼져있다 라고 해석 가능
모집단, 표본..?
- 모집단 : 조사하고 싶은 전체 대상
- 표본 : 모집단에서 일부만 뽑은 집단
- 표본평균 : 뽑은 표본의 평균값
- 표본분포 : 표본이 흩어져 있는 정도
- 표본평균의 분포 : 여러 표본의 평균을 모아 만든 분포.
= 데이터가 충분한 경우 정규분포를 따름
정규분포란? 평균을 중심으로, 좌우 대칭에, 종모양이며, 확률 예측이 가능 - 표준오차 : 표본의 표준편차 = 표본평균의 평균과 모평균의 차이
EX) 모평균이 70, 표본평균은 67, 표준오차는 3
정규분포
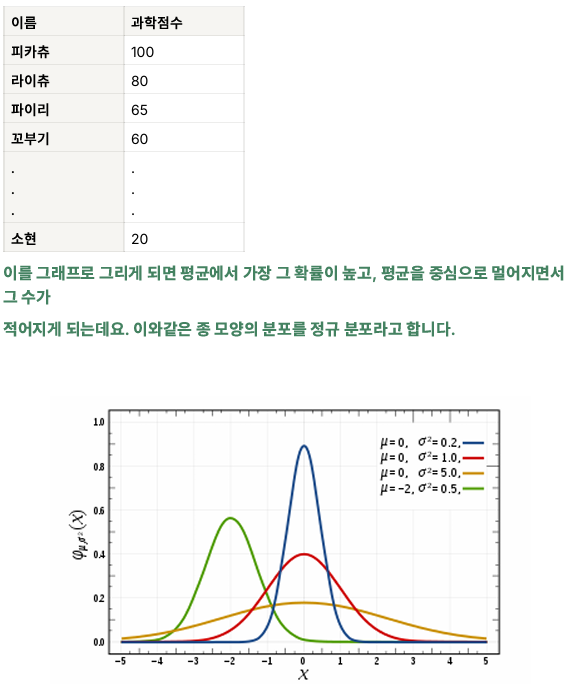
정규분포의 특징
1. 분포는 평균을 중심으로 좌우 대칭의 형태
2. 곡선은 각 확률값, 모두 더하면 1(100%)이 됨
3. 정규분포는 평균과 분산에 따라 다른 형태를 가짐
4. 평균 0, 분산 1을 가지는 경우, 이를 표준정규분포라고 함. (그림의 붉은색 그래프)
신뢰구간, 신뢰수준
신뢰구간 : 특정 범위 내에 값이 존재할 것으로 예측되는 영역
신뢰수준 : 실제 모수를 추정하는데 몇 퍼센트의 확률로 신뢰구간이 실제 모수를 포함하게 되는 확률 (95%,99% 주로 이용)
- 신뢰수준 95% : 무작위로 표본을 추출했을 때, 100번 중 95번은 신뢰구간 안에 모집단의 값을 포함
- 신뢰수준 99% : 무작위로 표본을 추출했을 때, 100번 중 99번은 신뢰구간 안에 모집단의 값을 포함
EX) 30명의 표본 평균이 78.4일 때, 95% 신뢰구간은 75.2~81.6
가설검정
- 어떤 주장을 통계적으로 맞는지 판단하는 법
귀무가설 = 일단 아무런 차이가 없다고 가정
EX) 효과 없음, 변화 없음, 차이 없음
대립가설 = 증명하고자 하는 가설
EX) 효과 있음, 변화 있음, 차이 있음
유의수준 = 우연으로 보기엔 너무 희귀한 상황의 기준. 보통 0.05(5%)를 사용.
-> 대립가설을 채택할 확률
P값(p-value) = 어떤 사건이 우연히 발생할 확률 (0이상, 1이하의 값)
- p-value가 0.05보다 작다 = 우연히 일어났을 가능성이 거의 없다 = 인과관계가 있다고 추정
=> 대립가설 채택 - p-value가 0.05보다 크다 = 우연히 일어났을 가능성이 높다 = 인과관계가 없다고 추정
=> 대립가설 기각
