Week02 | Generative Adversarial Network (2)
0. Prerequisite
Gan을 사용하는 과정에서 어떤 점이 문제가 되었고 어떻게 개선해 나갔는지에 대해 서술하였습니다.
01.1 problem
GAN의 판별자 D는 real or fake를 판단하기 때문에 BCE loss를 사용합니다. GAN을 실제로 구현 할때, discriminator하고 generator를 각각 따로 학습을 하게 됩니다. 그러다 보니 둘의 학습의 정도에는 차이가 있을 수 있습니다. 만약, discriminator가 너무 학습이 잘 되어서 완벽하게 generate된 이미지를 구분할 수 있는 경우를 생각해보도록 하겠습니다. generator는 어떠한 이미지를 내더라도 discriminator를 속일 수 없고, 더이상 학습이 진행이 되지 않을 것입니다. 반대의 경우도 마찬가지 입니다. 한쪽이 너무 잘 되어버리면 다른 쪽은 학습이 더이상 진행이 되지 않고 멈추어버리게 됩니다. 이렇게 되면 generator는 한 종류의 이미지만 계속 생성하게 됩니다. (mode collapse 발생)
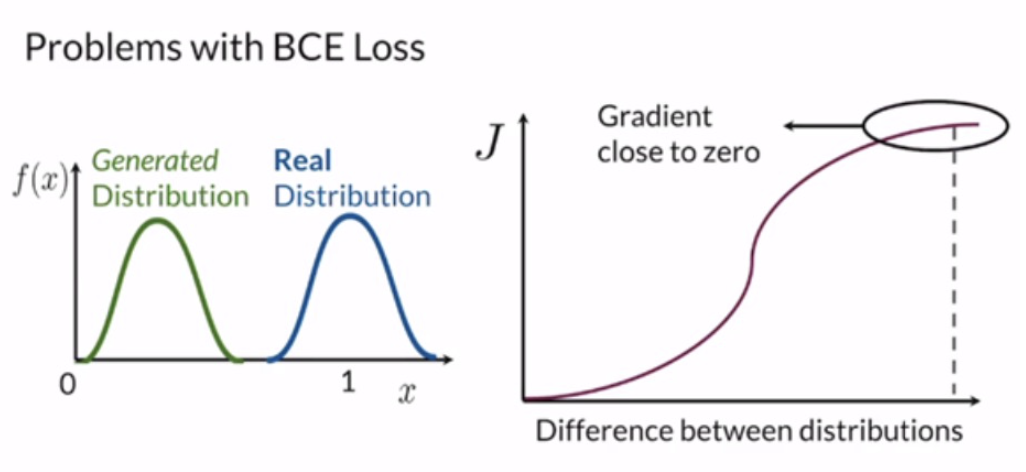
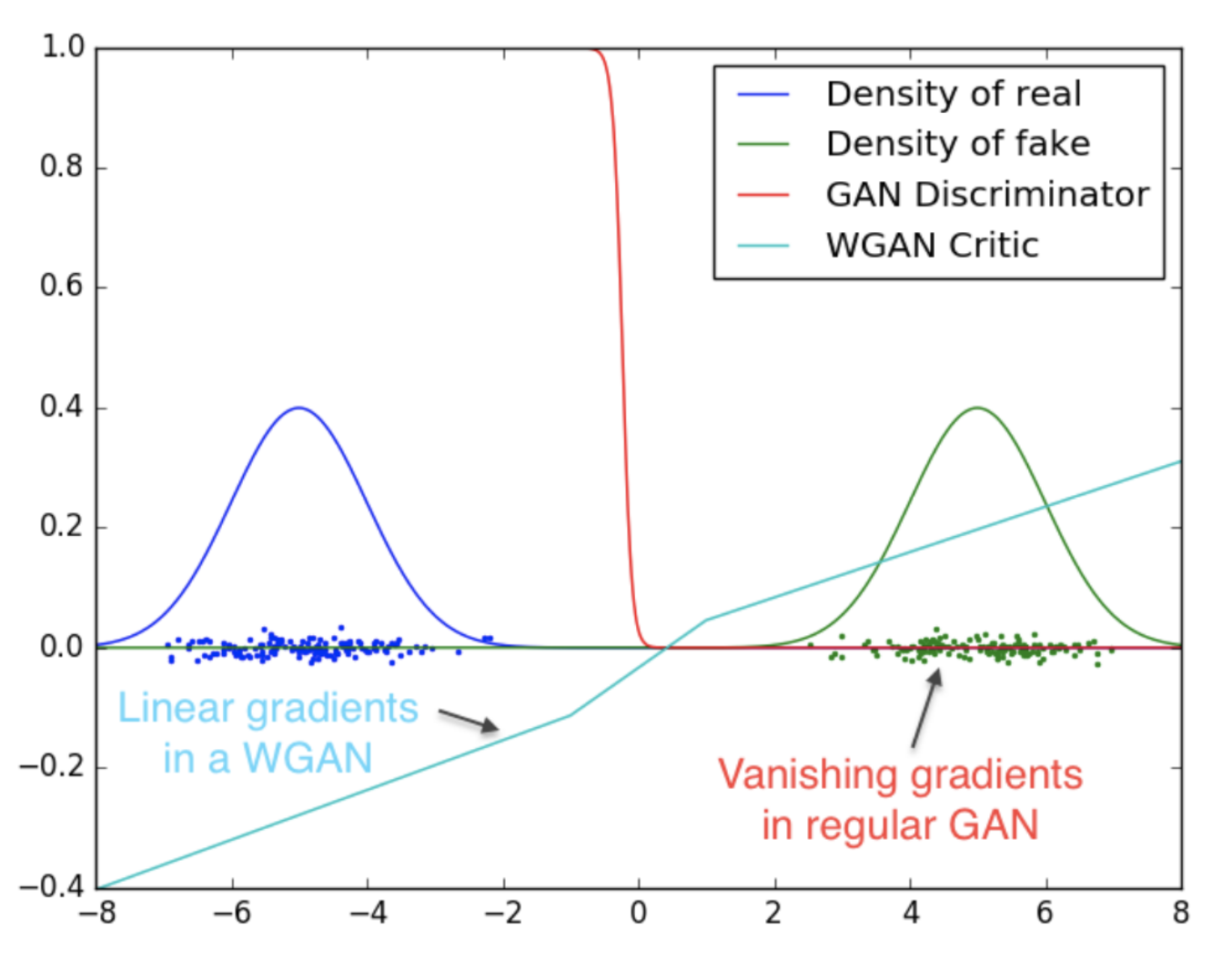
판별자 D는 sigmoid를 사용하여 real/fake의 확률값을 출력으로 합니다. 따라서 판별자가 좋아짐에 따라 두 분포의 차이가 심해져서 cost funtion의 기울기가 0값인 영역에 위치해 이처럼 vanishing gradient문제가 생깁니다.
이러한 문제는 GAN에서는 흔한 일입니다. 이를 어떻게 해결해야할까요?
01.2 solution
이를 해결하기 위해서는 새로운 cost function을 위한 새로운 방법을 도입해야합니다. 이를 위해 아래에 설명된 Earth-Mover (EM) distance/ Wasserstein Metric 를 사용하게 됩니다. 이를 예시와 함께 쉽게 설명한 글이 있어 참고해 작성하였습니다. (하단 링크 첨부)
Earth-Mover (EM) distance/ Wasserstein Metric
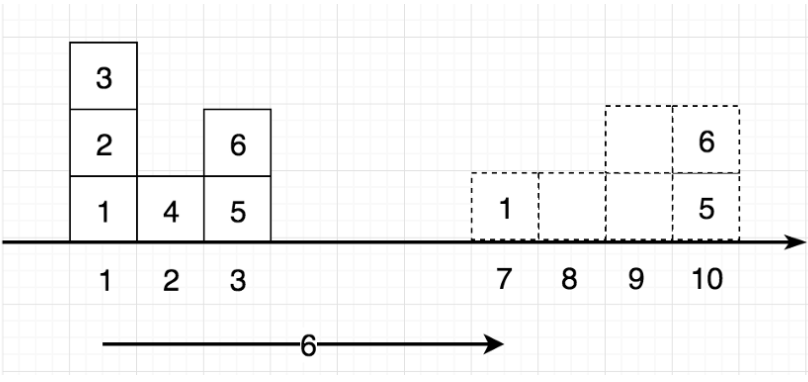
왼쪽의 6개 박스를 오른쪽에 점으로 표시된 위치로 옮기고 싶습니다.
1번 상자의 경우 위치 1에서 위치 7로 이동합니다.
이 때, 이동 비용은 무게에 거리를 곱한 값과 같습니다. "모든 상자"의 무게를 1로 설정하면 1번 상자를 옮기는 비용은 6(7–1)과 같습니다.
아래 그림은 두 가지 다른 이동 γ를 나타냅니다. 오른쪽에는 상자가 이동하는 방법을 정리해 표로 나와 있습니다.
어떻게 상자의 이동을 표로 나타낼까요? 예를 들어, 첫 번째 그림에서 2번 상자와 3번 상자를 위치 1에서 위치 10으로 옮깁니다. 따라서 표에서 항목 (1, 10)에는 2가 들어갑니다. 아래 두 가지 박스 이동의 총 운송 비용은 모두 42입니다.
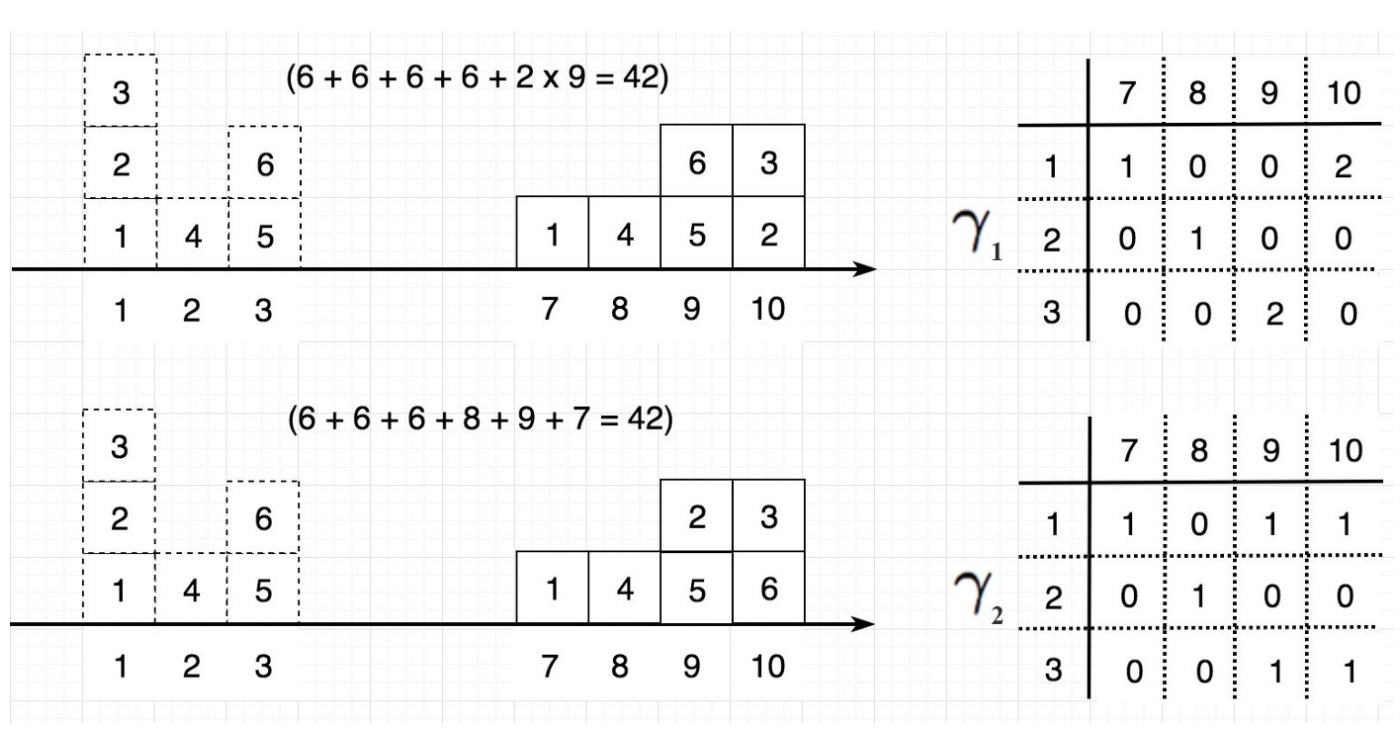
그러나 모든 박스의 이동이 동일한 비용을 부담하는 것은 아닙니다. Wasserstein distance(또는 EM distance)는 가장 비용이 적게 들어 갑니다. 아래 예제에서 두 박스 이동은 서로 다른 비용을 가지며 Wasserstein distance(최소 비용)는 2입니다.

Wasserstein distance는 데이터 분포 q를 데이터 분포 p로 변환할 때 드는 최소 비용입니다. 실제 데이터 분포 Pr과 생성된 데이터 분포 Pg에 대한 Wasserstein distance는 수학적으로 모든 박스의 이동에 대한 최소 비용으로 정의됩니다.
(참고: 집합 X의 하한을 inf 라고 한다.)
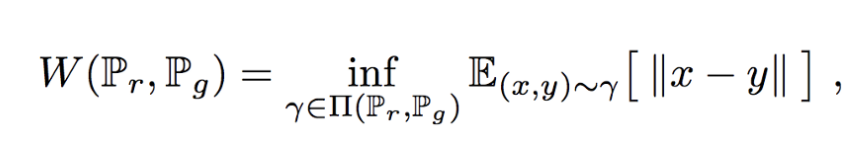
이 식에서 Π(Pr, Pg)는 한계값이 각각 Pr과 Pg인 모든 분포를 나타냅니다. 자세히 설명하자면 위에서 설명한 그림에서

두 가지 경우 모두 박스를 옮기고 난 뒤의 형태가 같죠. 이렇게 동일한 형태로 다르게 옮기는 방법은 위 두 가지 외에도 많은 경우의 수가 존재합니다. 즉, Π는 옮기고 난 뒤에 형태가 같은 모든 경우를 의미합니다.
새로운 비용함수를 좀 더 살펴보기 전에 KL-Divergence 와 JS-Divergence 를 다시 한 번 짚고 넘어가겠습니다.
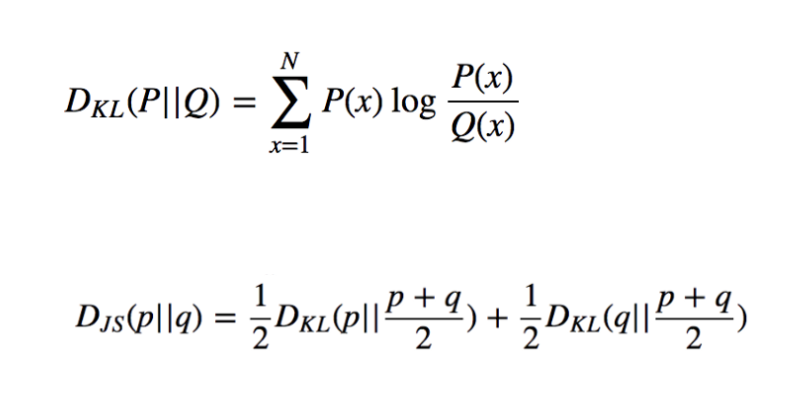
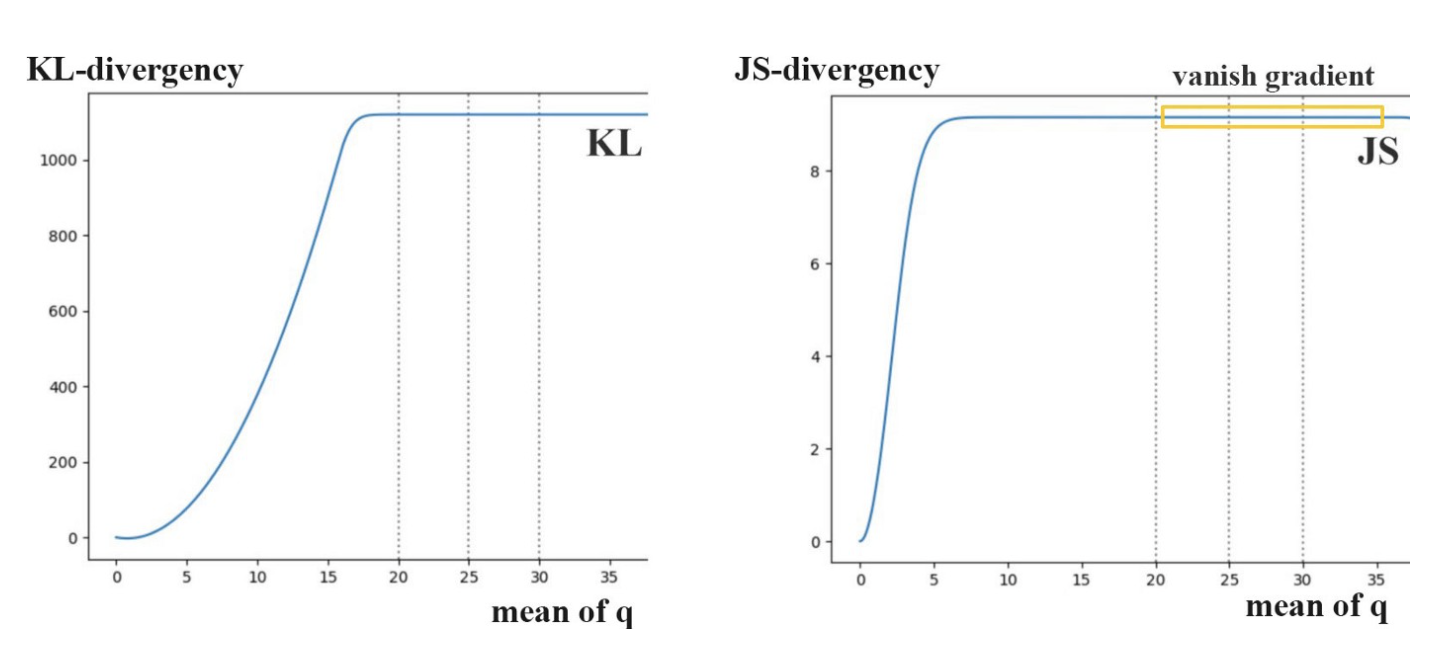
여기서 p는 실제 데이터 분포이고 q는 모형에서 추정된 분포입니다. 아래 다이어그램에서는 p와 평균이 다른 여러 개의 q를 표시합니다.

0에서 35 사이의 평균을 사용하여 p와 q 사이의 해당 KL-divergence 및 JS-divergence를 표시했을 때, 예상대로 p와 q가 모두 같으면 분산은 0입니다. 또한 q의 평균이 증가할수록 분산이 증가합니다. 즉, divergency의 기울기는 결국 줄어듭니다. 우리는 거의 0의 구배를 가지고 있다. 즉, 앞에서 언급했듯 vanishing gradient문제가 생깁니다. 실제로 GAN은 generator보다 discriminator를 더 쉽게 최적화할 수 있습니다. 따라서 너무 잘 판별하게 되고 더 이상 학습이 진행이 되지 않
을 가능성이 큽니다.
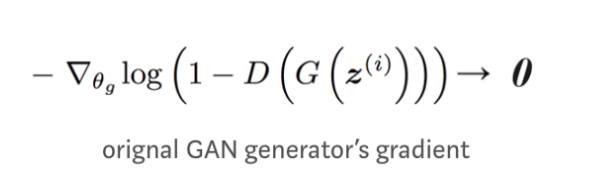
원래의 GAN 논문은 이 그레이디언트 소실 문제를 해결하기 위한 대체 비용 함수를 제안합니다. 그러나 Arjovsky는 새로운 함수가 모델을 불안정하게 만드는 gradient의 큰 분산을 가지고 있음을 보여줍니다.

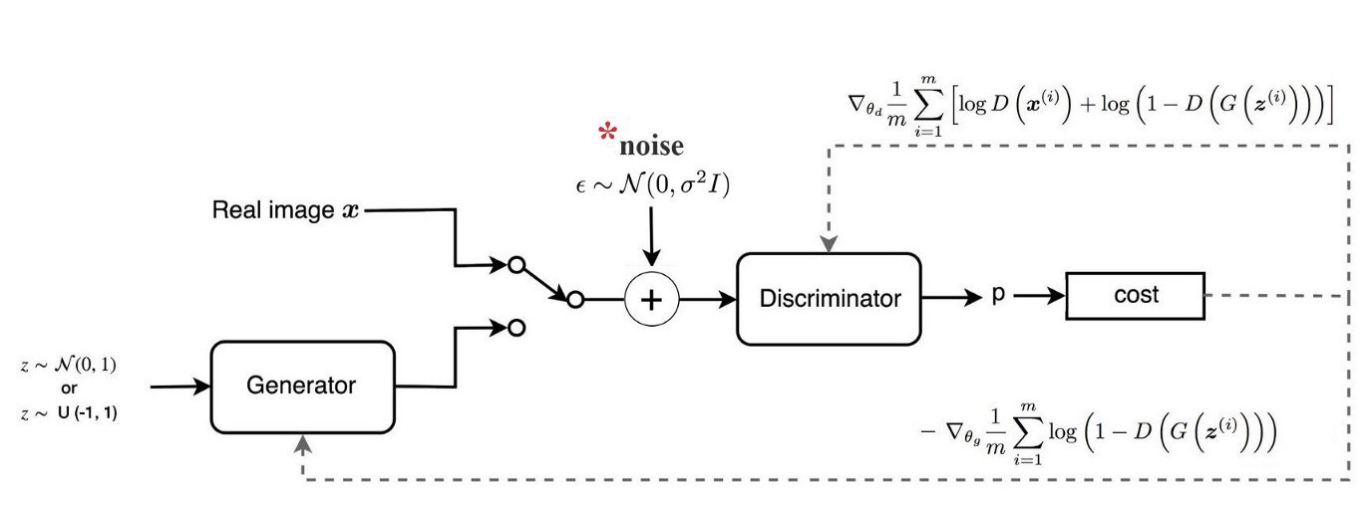
Arjovsky는 모델을 안정화하기 위해 생성된 이미지에 노이즈를 추가할 것을 제안하였습니다.
Wasserstein Distance
Wasserstein GAN (WGAN)은 노이즈를 추가하는 대신 모든 곳에서 부드러운 기울기를 갖는 Wasserstein 거리를 사용하는 새로운 비용 함수를 제안합니다. WGAN은 generator가 실행 중이든 실행 중이든 관계없이 학습합니다.
그러나 Wasserstein distance에 대한 방정식은 매우 다루기 어렵습니다. Kantorovich-Rubinstein 이중성을 사용하여 다음과 같이 계산을 단순화할 수 있습니다.
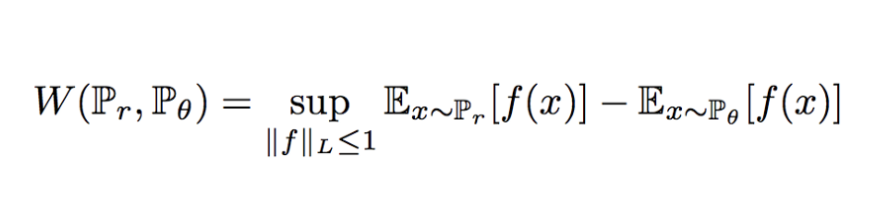
(참고: 여기서 sup은 최소 상한이고 f는 제약조건에 따른 1-Lipschitz function이다.)
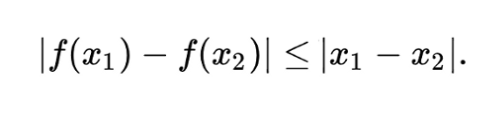
그래서 Wasserstein distance를 계산하기 위해, 우리는 단지 1-Lipschitz function를 찾으면 됩니다. 다른 딥러닝 문제처럼 깊은 네트워크를 구축할 수 있습니다. 실제로, 이 네트워크는 시그모이드 함수 없이 판별기 D와 매우 유사하며 확률보다는 스칼라 점수를 출력합니다. 이 점수는 입력이 얼마나 실제와 가까운지 해석할 수 있습니다. 강화 학습에서, 이것을 상태(입력)가 얼마나 좋은지를 측정하는 value function이라고 부릅니다.
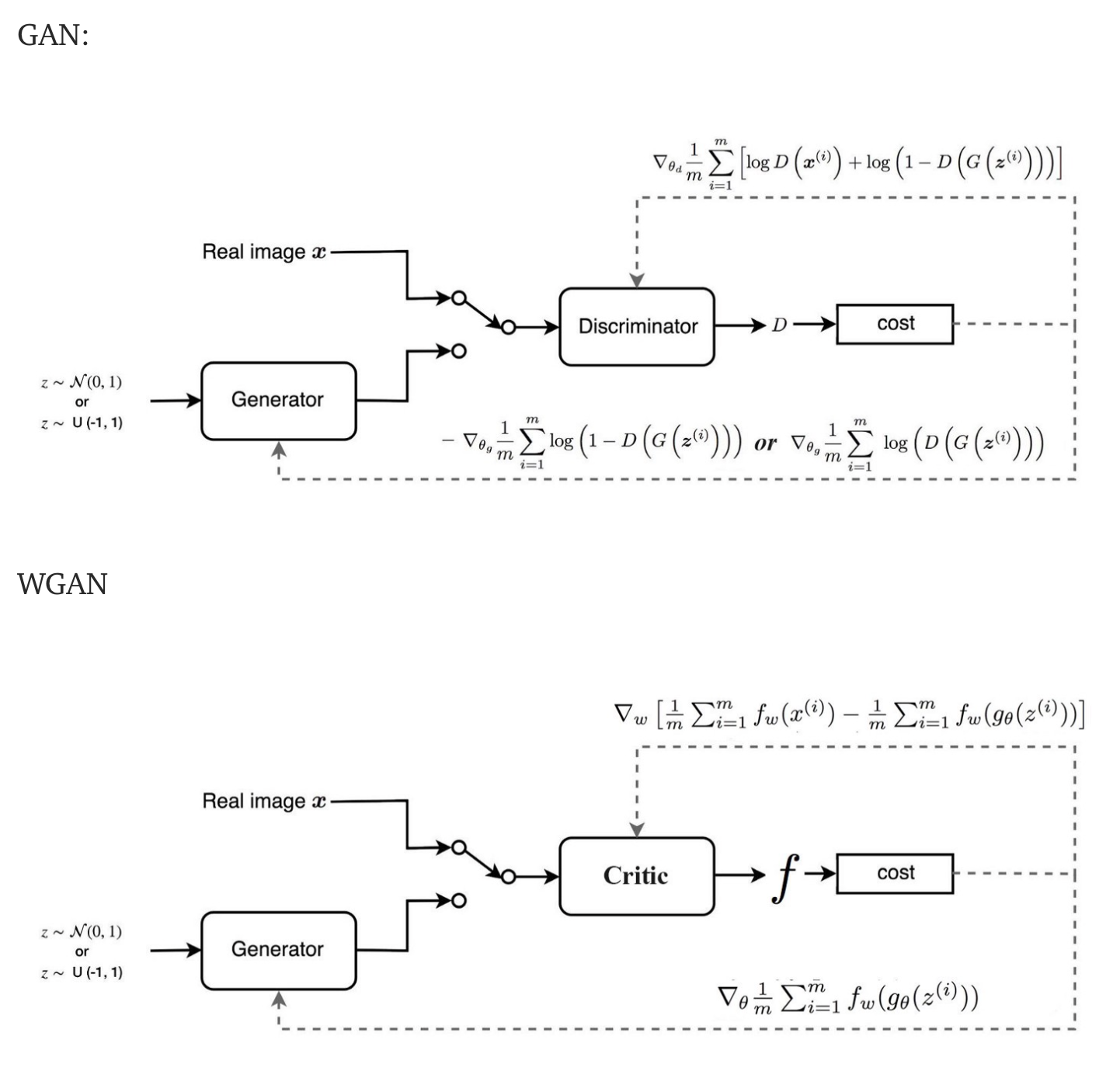
여기서 f는 1-Lipschitz function이어야 합니다. 제약 조건을 적용하기 위해 WGAN은 매우 간단한 클리핑을 적용하여 f의 최대 가중치를 제한합니다. 즉, 판별기의 가중치는 hyper parameter c에 의해 제어되는 특정 범위 내에 있어야 합니다.
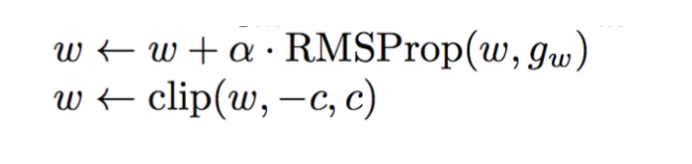
읽어보면 좋을 자료
Gan들의 여러 issue들과 설명이 자세히 되어 있으니 꼭 읽어보시길 추천드립니다.
https://jonathan-hui.medium.com/gan-gan-series-2d279f906e7b
이후 다른 gan에서의 문제점과 해결책에 대해 추가해두겠습니다!
감사합니다.
Reference
https://jonathan-hui.medium.com/gan-wasserstein-gan-wgan-gp-6a1a2aa1b490
Lipschitz 제약에 대한 추가 설명
https://jonathan-hui.medium.com/gan-spectral-normalization-893b6a4e8f53
