1. Limitations of GNN

문제점과 해결 방법

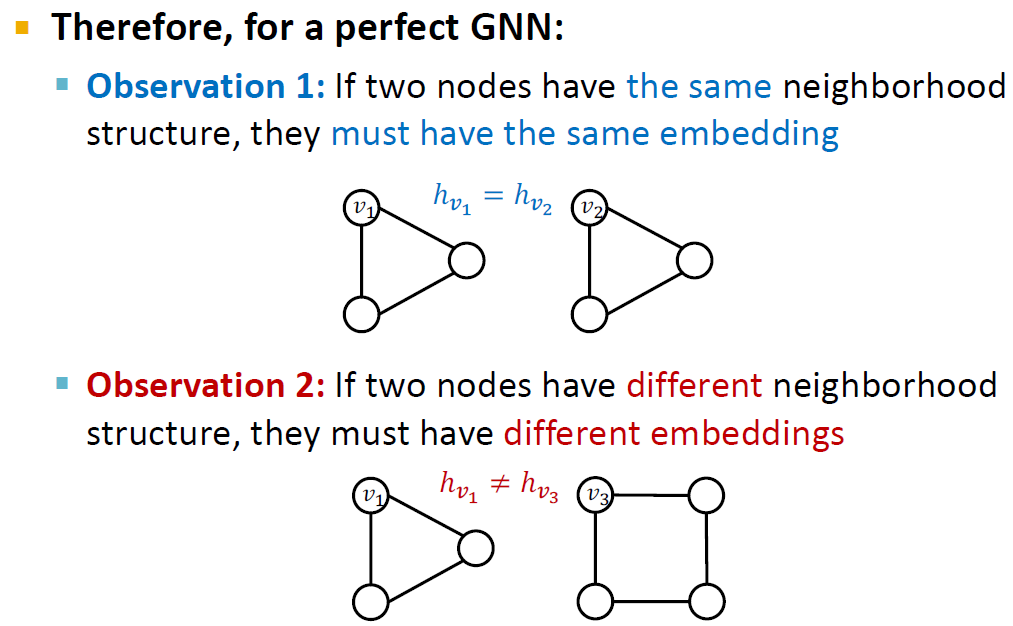
완벽한 GNN 모델이란, 1) 두 노드가 같은 neighborhood structure를 가지면 같은 임베딩을 가지고, 2) 다른 neighborhood structure를 가지면 다른 임베딩을 가지는 것을 의미합니다.

하지만, 이 두 가지 경우에는 문제점이 있습니다.

첫번째 경우에는, 서로 다른 두 노드가 같은 neighborhood structure를 가질 때 서로 다른 임베딩을 할당할 수 없다는 것입니다. 이런 task를 Position-aware tasks 라고 지칭합니다.

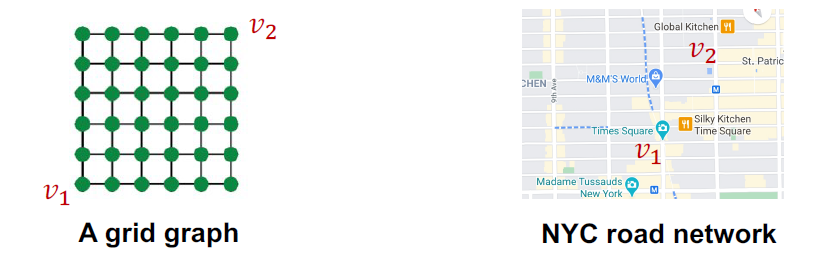
이 그림에서 $v_1$과 $v_2$는 지도 위에서 서로 구분되어야 하는 다른 점이지만, 같은 neighborhood structure를 가집니다.

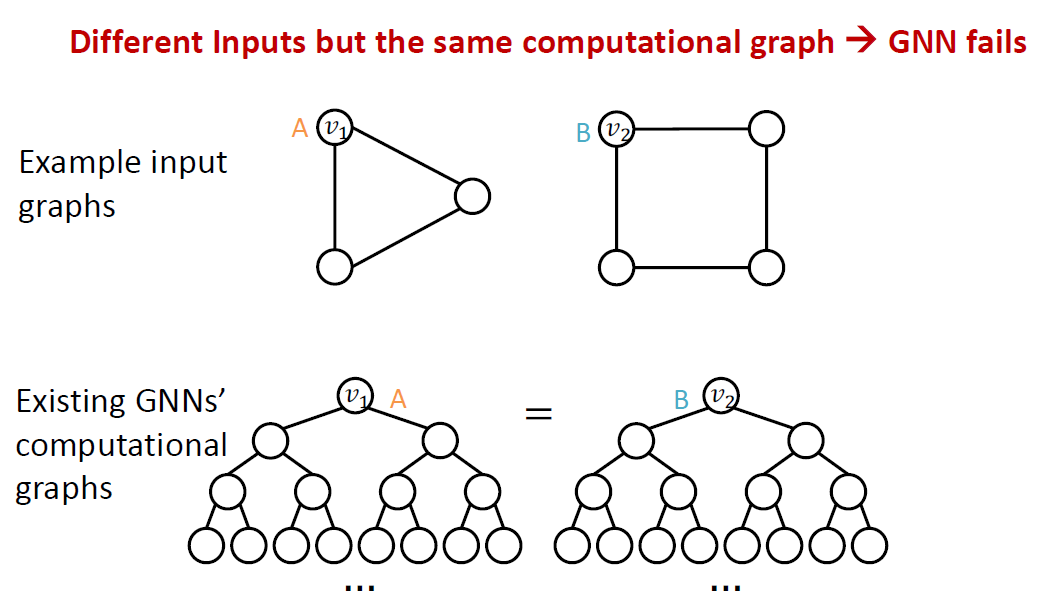
두번째 경우의 문제점도 존재합니다. Message passing GNN같은 경우에는 cycle length를 구별하지 못합니다.

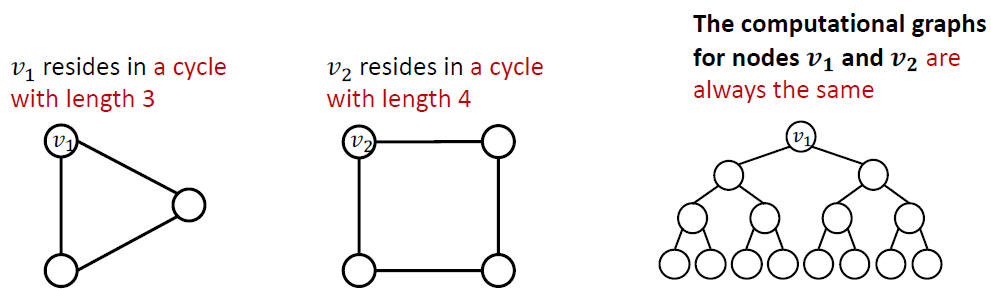
$v_1$과 $v_2$는 다른 cycle length를 가지고 있지만 computational graph는 같습니다.

두 경우의 문제를 해결하기 위한 방법이 각각 존재합니다. 첫번째 경우에 대한 해결 방법은 그래프 안에서 노드가 가지는 위치를 고려하여 노드 임베딩을 만드는 것입니다. Position-aware GNN이 예시입니다.

두번째 경우에 대한 해결 방법은 9강에서 배웠던 WL test보다 더 expressive한 message passing GNN을 만드는 것입니다. Identity-aware GNN이 그 예시입니다.

접근 방법

기본적인 아이디어는 성공적인 그래프 모델이라면 서로 다른 두개의 input(node, edge, graph)를 서로 다르게 라벨링해야 한다는 것입니다.
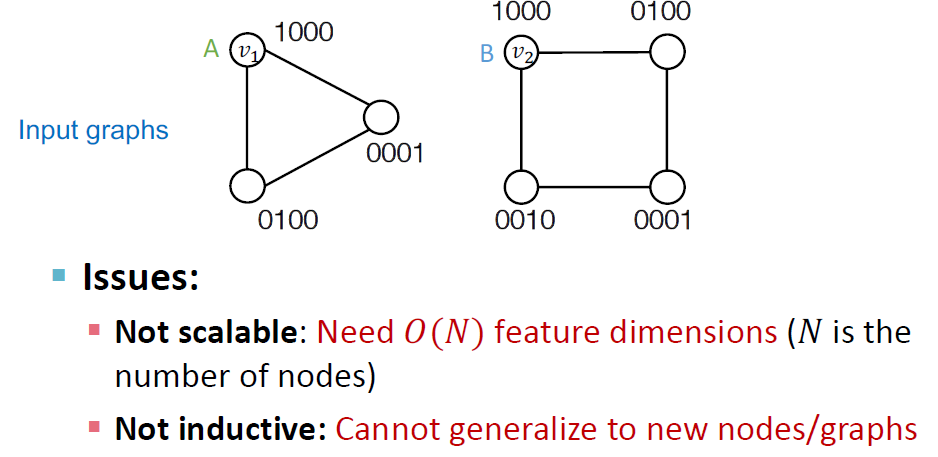
한 가지 naive한 해결방법은 모든 노드를 서로 다른 id로 인코딩하는 방법입니다. 이렇게 되면 , 모든 노드의 id를 모아 원핫인코딩을 해야 합니다. 이 방법은 당연하게도 좋은 방법이 아닙니다.

2. Position-aware GNN

Position information encoding

첫번째 경우의 해결 방법인 Position-aware GNN부터 살펴보겠습니다.
그래프에는 두 가지 종류의 task가 있습니다. Structure-aware task에서는 노드가 구조적인 역할에 의해 라벨링되고, Position-aware task 에서는 노드의 위치에 따라서 라벨링됩니다.

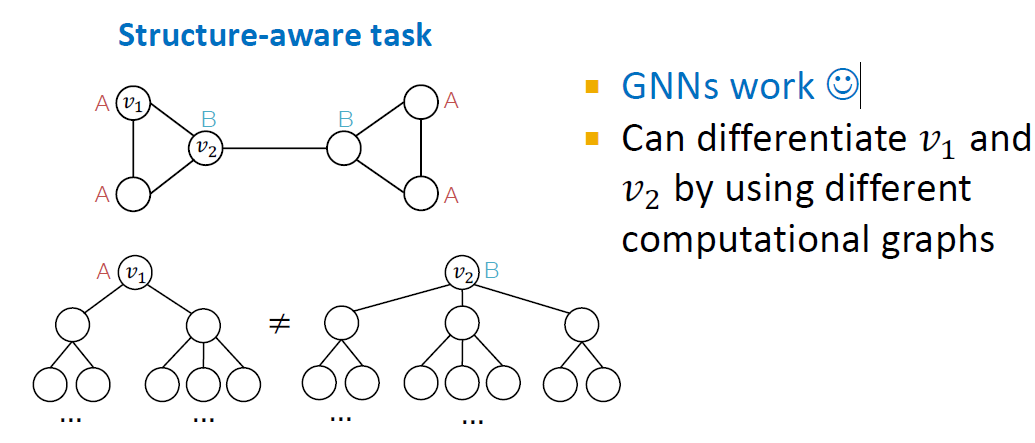
Structure-aware task(A,B의 구분이 structure aware인 경우)에서는 GNN이 대부분 성공적인 모델입니다. 이 예시에서는 $v_1$과 $v_2$의 computational graph가 다르기 때문에 $v_1$(A)과 $v_2$(B)가 잘 구별되었습니다.

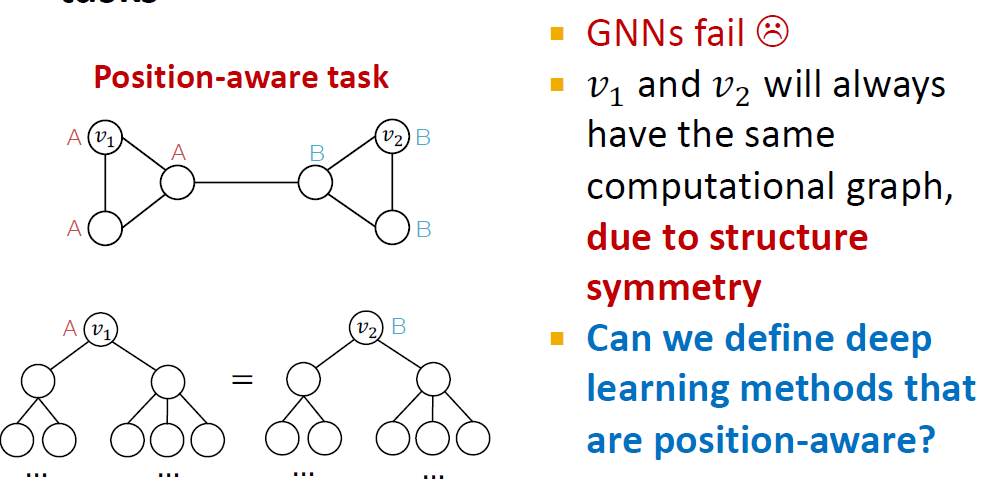
하지만 position-aware task에서 GNN은 실패하는 경우가 많습니다. $v_1$과 $v_2$가 같은 computational graph를 가지기 때문에 A와 B가 구별되지 않습니다.

따라서, position-aware task의 문제점을 해결하기 위해 Anchor라는 개념을 도입합니다.

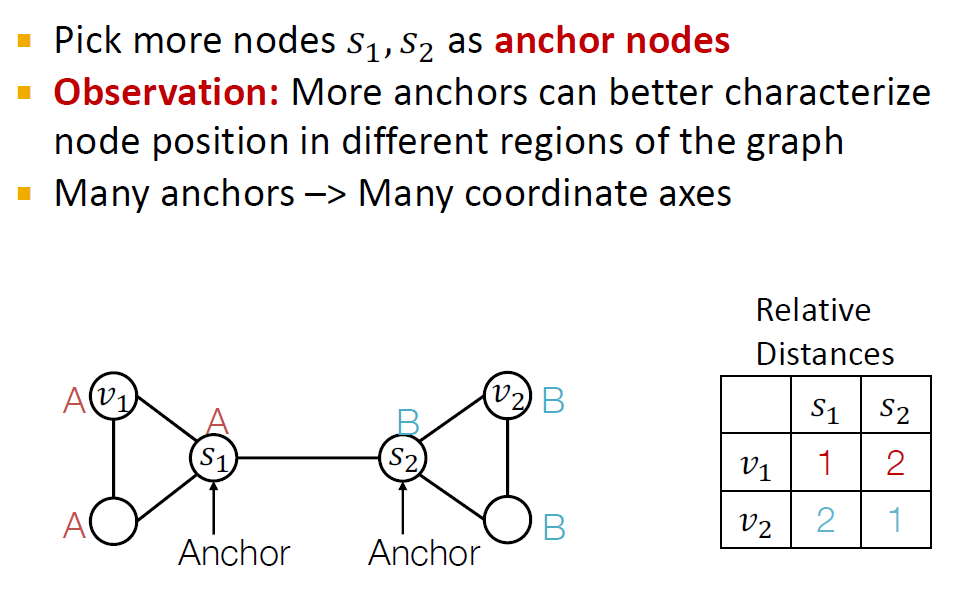
anchor에 해당하는 $S_1$과 $S_2$를 랜덤하게 정한 후, $v_1$, $v_2$와의 상대적 거리를 계산합니다. S_1에서 v_2까지의 거리는 2 hop, S_2에서 v_1까지의 거리는 1 hop 입니다.

여러 노드가 anchor가 되는 Anchor set를 구성할 수도 있습니다.

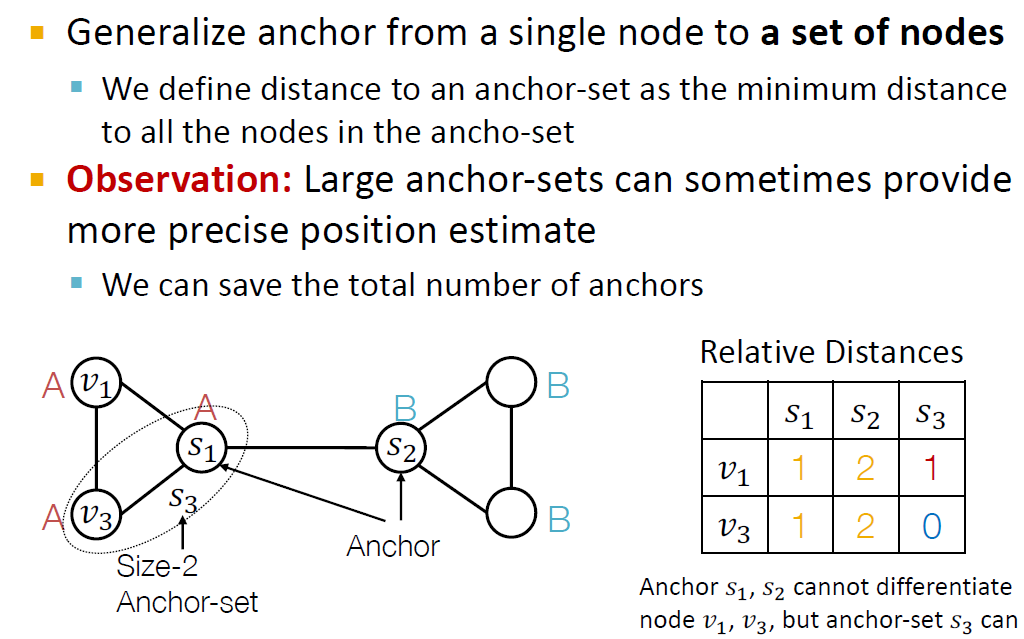
노드에서 anchor set까지의 거리는 anchor set에 속하는 모든 노드와의 거리 중 최솟값에 해당합니다.
이 경우에 S_3에서 v_1까지의 거리는 1 hop입니다.
Anchor set를 이용한 방법에서 v_1의 position encoding은 (1,2,1), v_2는 (1,2,0)이 됩니다.

Position 정보를 사용하는 방법

간단한 방법은 position 인코딩을 augmented node feature로 사용하는 것입니다. position 인코딩의 각 차원이 랜덤한 anchor에 관련지어지기 때문에 positional 인코딩의 차원이 랜덤하게 변경되지만, 의미상의 변화는 없을 것입니다.
더 나아가, position encoding의 permutation invariant property를 유지하는 NN 구조를 만드는 방법도 존재합니다. input feature의 차원을 바꾸는 것은 output 차원에만 변화를 주고, 각 차원의 값은 바뀌지 않을 것입니다. (자세한 내용은 position aware GNN 논문 참조)

3. Identity-aware GNN

Structure-aware task에서 GNN이 대부분의 경우에 문제가 없다고 앞서 언급했지만, 항상 완벽한 것은 아닙니다.
Structure-aware task에서 GNN의 실패 사례는 1)Node level, 2) Edge level, 3)Graph level로 나눌 수 있습니다.

1) Node level

$v_1$은 A, $v_2$는 B에 해당하지만 node level에서의 computational graph는 동일합니다. 따라서 이 경우에 $v_1$과 $v_2$는 구별되지 않는다는 문제가 발생합니다.

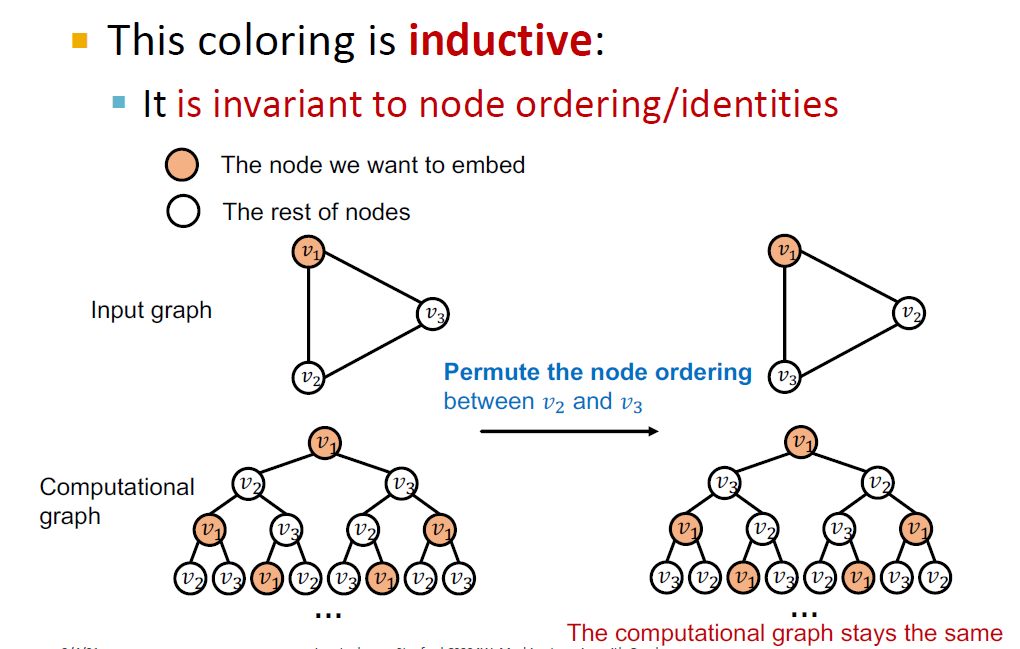
이 경우에 해결책은 우리가 임베딩하고 싶은 노드에 색을 지정하는 것입니다. 이 경우, 먼저 같은 노드($v_1$)를 임베딩하고자 할 때 이웃 노드($v_2,v_3$)의 순서가 바뀌어도 임베딩이 동일합니다. 따라서 이웃 노드에 순서에 영향을 받지 않는다는 것을 알 수 있습니다. 이 성질은 모델의 일반화 성능에 도움이 됩니다.

반면, 다른 노드에 대해서는 서로 다른 computational graph를 만들어냅니다. 두 computational graph는 가장 아래 레이어의 노드 색이 서로 달라 구별됩니다.
따라서, 노드에 색을 지정하는 방식은 Node level에서 같은 노드는 같게(더 robust한 일반화), 다른 노드는 다르게 임베딩할 수 있게 합니다.

2) Edge level

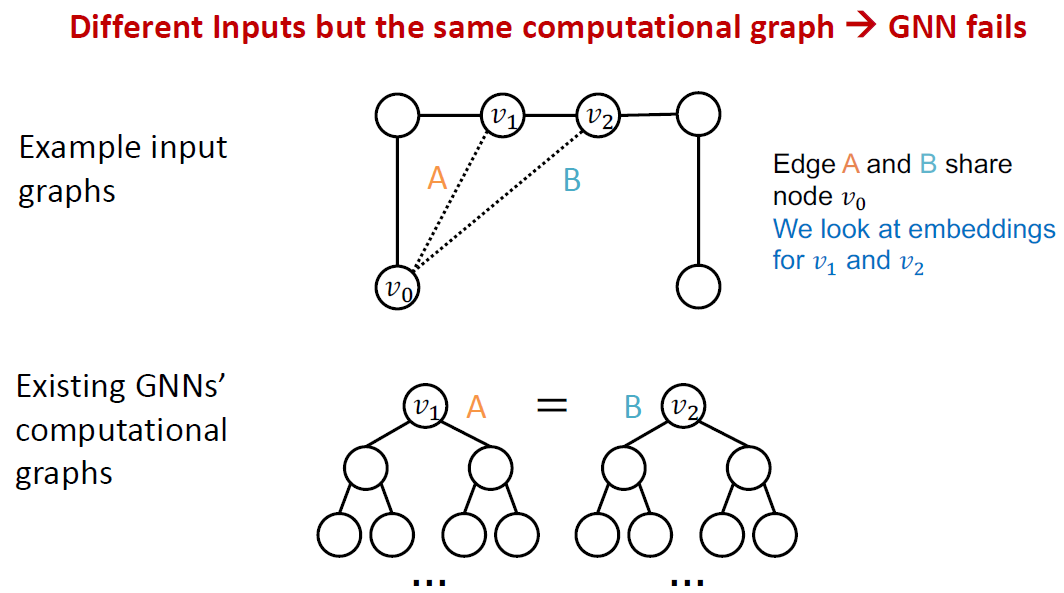
edge level에서도 두 edge A와 B는 서로 다르지만, computational graph는 동일하다는 문제점이 있습니다.

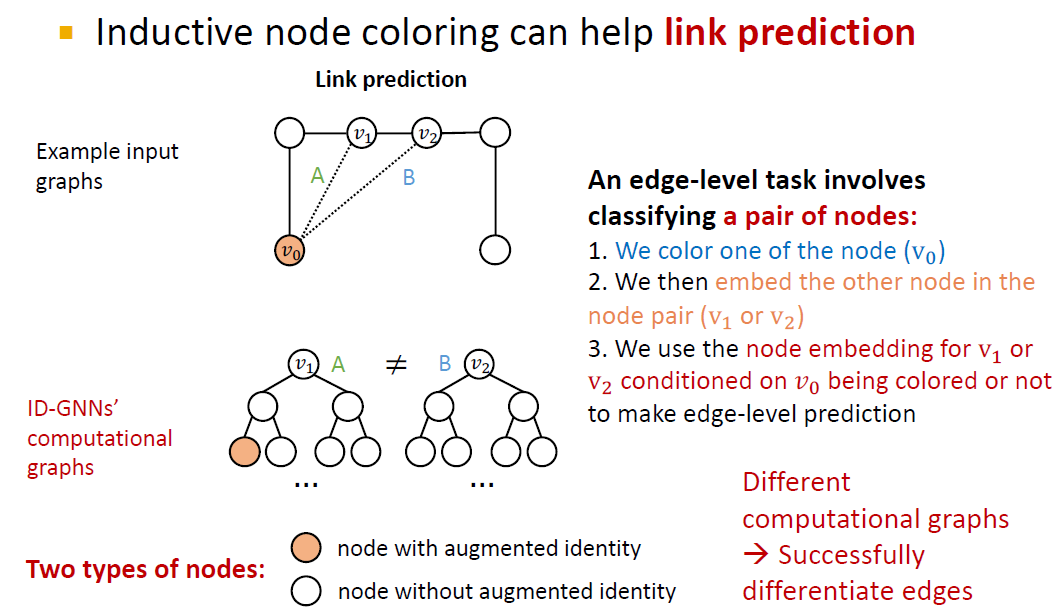
이 경우에도 node coloring 방법을 이용하면 A와 B edge에 대해 서로 다른 computational graph를 형성할 수 있습니다.

3) Graph level

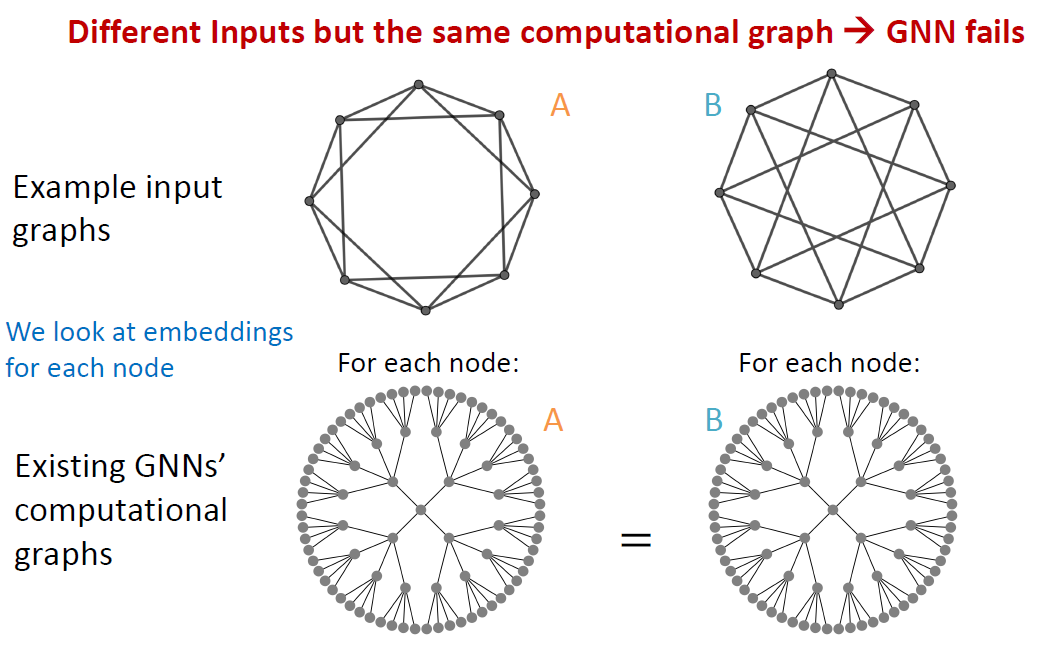
A와 B 그래프는 서로 다른 그래프이지만, computational graph를 만들었을 때, 구별되지 않는다는 문제점이 발생합니다.

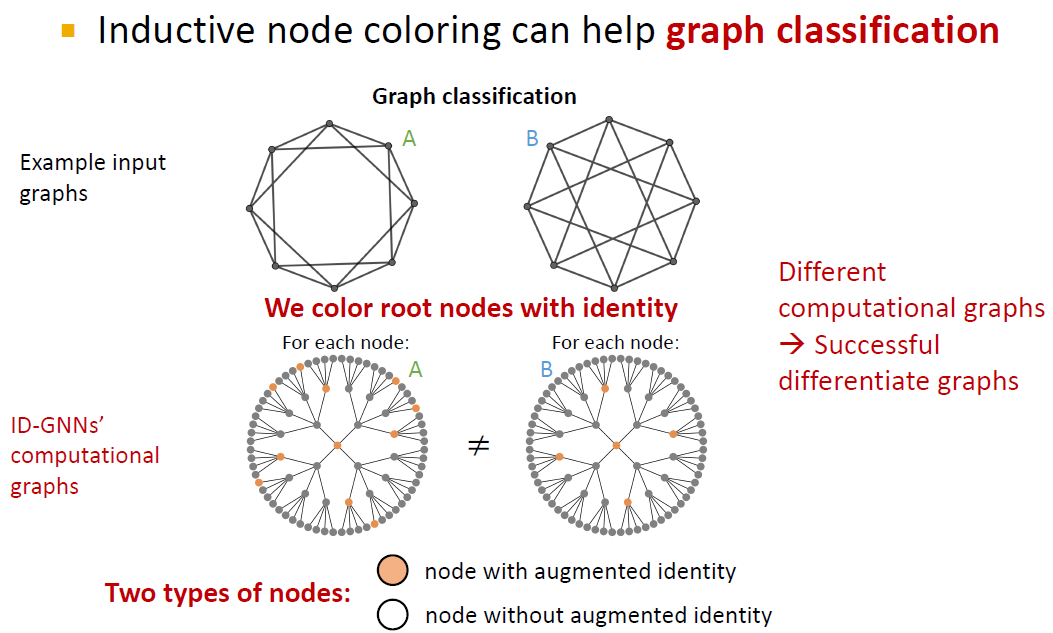
graph level에서도 node coloring 방법을 적용하면 두 그래프의 computational graph가 다르게 형성되어 구별됩니다.

Identity aware GNN

그렇다면, coloring 방법을 구현하는 방법에 대해서 알아보겠습니다.

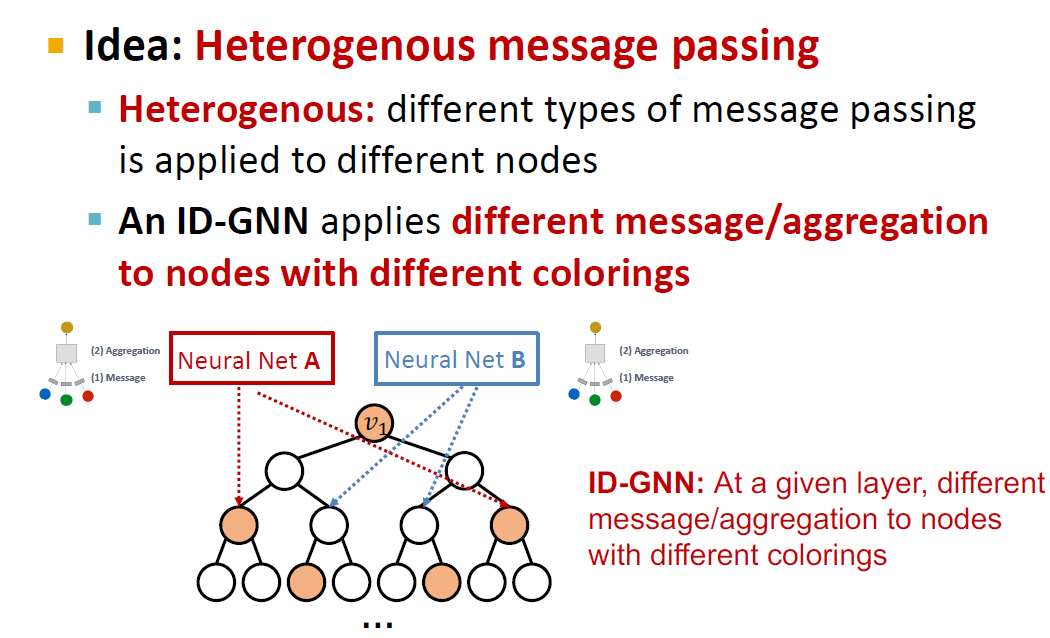
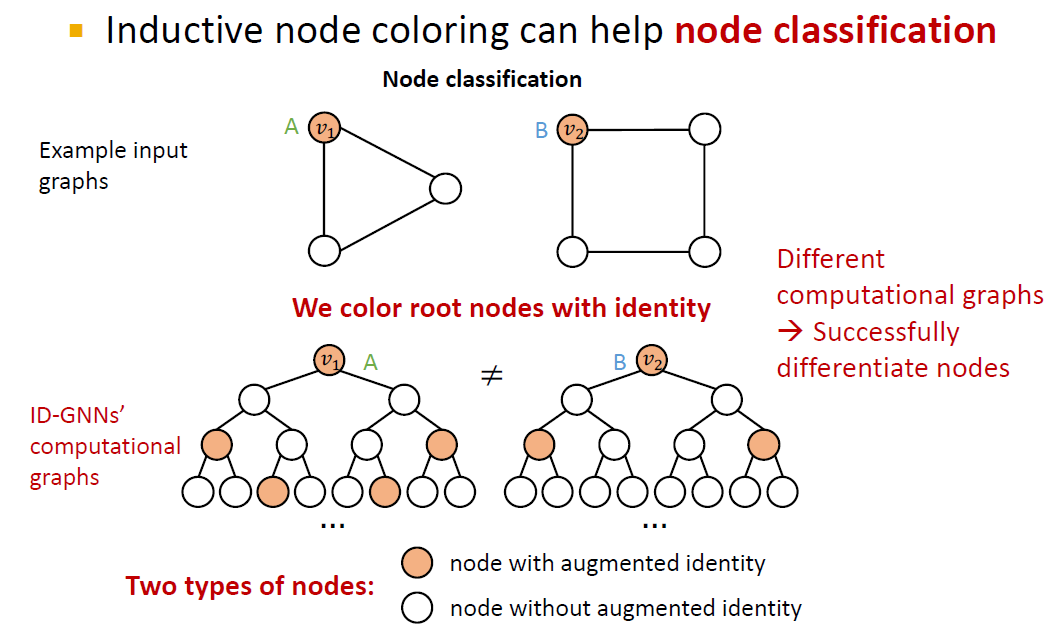
Heterogenous message passing이란, 서로 다른 노드에 다른 방법으로 message passing을 하는 것입니다. 여기서는 다른 색의 노드에 서로 다른 방법을 사용한다는 의미입니다.

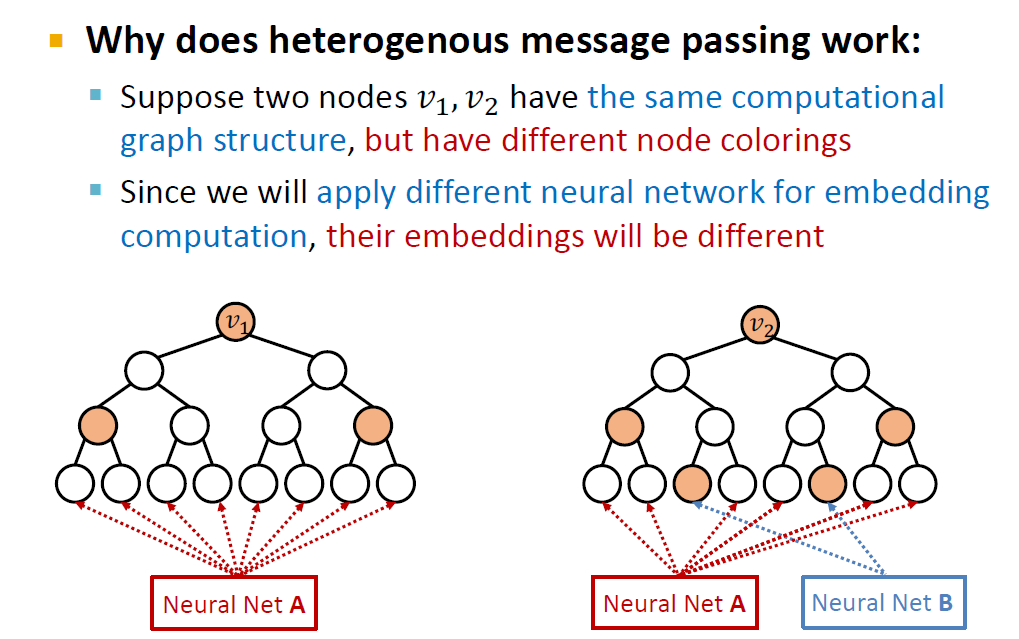
이것이 두 색의 노드를 구분하는데에 도움이 되는 이유는 v_1과 v_2가 같은 computational graph 구조를 가지고 있지만 다른 노드 색을 가질 경우, 각 노드의 색에 따라 다른 NN 임베딩을 적용하기 때문에 v_1과 v_2는 서로 다른 임베딩을 가질 것이기 때문입니다.

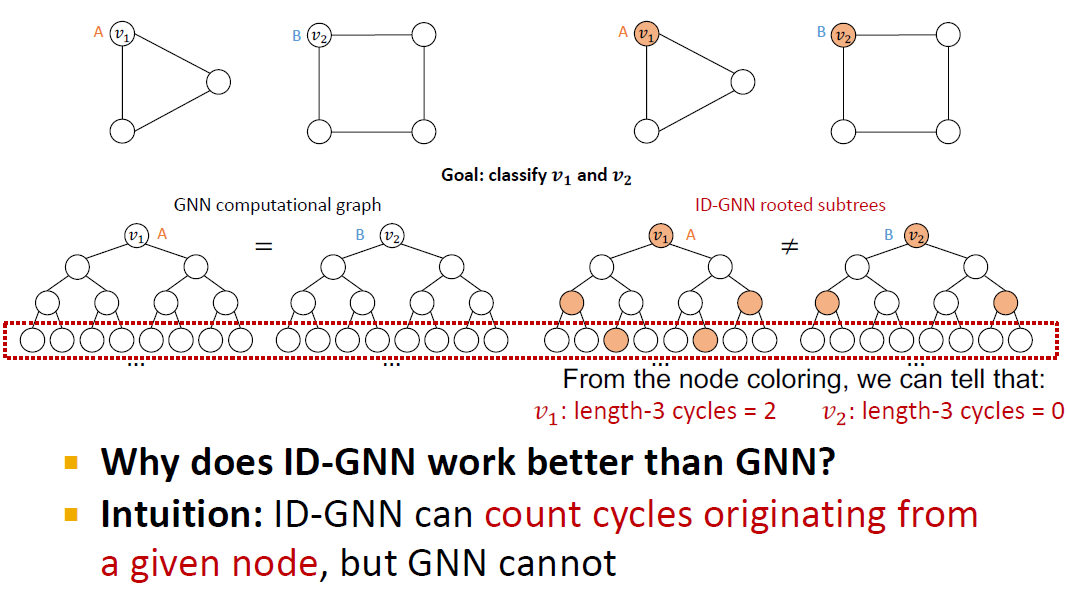
ID-GNN은 중심이 되는 노드(v_1,v_2)에 대한 cycle count를 계산할 수 있지만, GNN은 그렇지 않다는 점에서 ID-GNN이 더 우수하다고 할 수 있습니다.

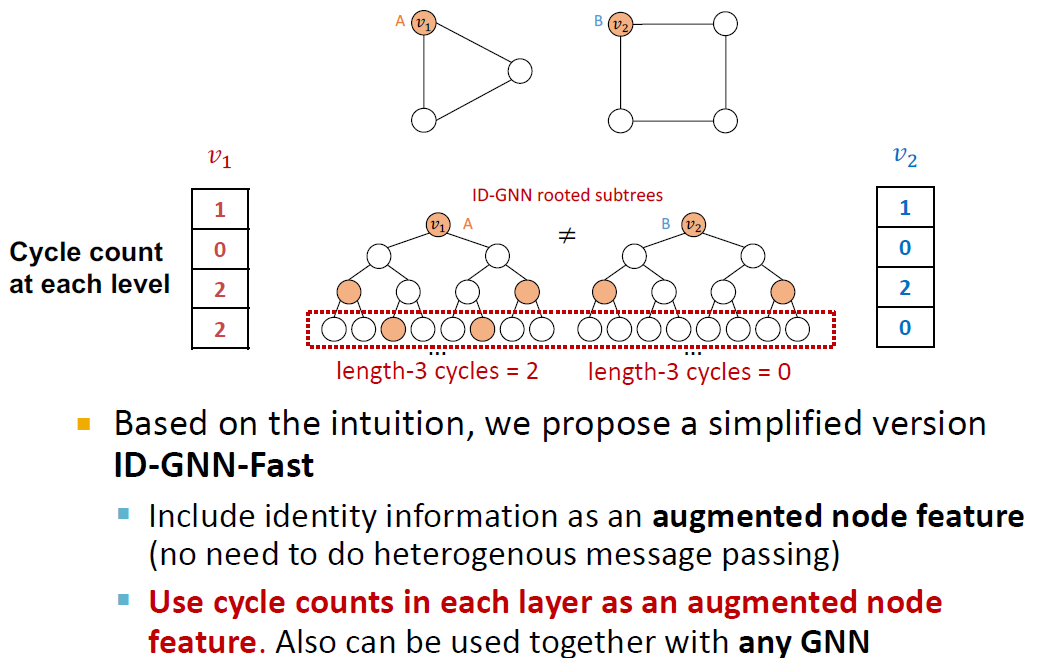
cycle count가 중요한 이유는 이것이 다른 방법으로도 유용하게 사용이 가능하기 때문입니다.
위의 예시에서 ID-GNN-Fast를 만들기 위해서 heterogenous message passing 대신에 각 그래프 level의 cycle count를 세어서 이것을 augmented node feature로 사용할 수 있습니다. 앞서 등장했던 방법보다 훨씬 간편하지만, v_1과 v_2가 서로 구별되므로 올바른 모델이라고 할 수 있습니다.

4. Robustness of GNN

1) adversarial attack possibilities

adversarial attack에는 Direct attack과 Indirect attack이 있습니다.

target node는 attacker가 label 예측값을 바꾸려고 하는 노드입니다. attacker node는 attacker가 직접 바꿀 수 있는 노드입니다.
Direct attack은 target 노드와 attacker 노드가 같은 경우입니다. 즉, attacker가 target 노드를 직접 조작할 수 있다는 의미입니다. 따라서 target 노드의 feature를 바꾸거나 target 노드의 connection을 추가 또는 삭제 할 수 있습니다.

indirect attack은 target node가 attacker node에 속하지 않는 경우, 즉, attacker가 target 노드를 직접 조작할 수 없는 경우에 해당합니다. 이 경우, attacker는 간접적으로만 그래프를 조작할 수 있습니다. attacker node의 feature를 변경하거나, attacker 노드와 연결된 엣지를 추가 / 삭제할 수 있습니다.

2) Mathmetically formalize the attack as an optimization problem

Adversarial attack 문제를 수학적으로 정의할 수 있습니다.

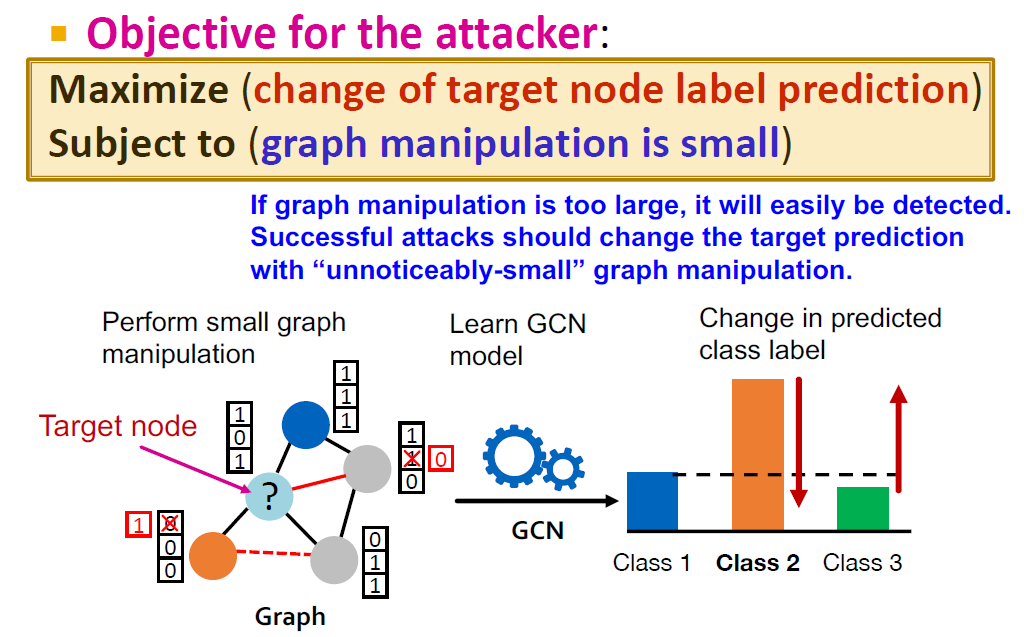
attacker의 목적은 조작이 발각되지 않는 한에서 최대한 결과물을 원래와 다르게 바꾸어놓는 것입니다. 이것을 수학적으로 접근하면, "target 노드의 label 예측값을 최대화하는데 그래프 manipulation이 적다는 제한조건이 있다" 라고 정의할 수 있습니다.

이것을 수식으로 정리하면 다음과 같습니다.


$\theta^*$ 는 조작 이전 (원래) 그래프에서 train loss를 최소화하는 파라미터의 추정값을 의미합니다.
$c^*_v$ 는 분류 확률을 최대화하는 class 예측값, 즉, 가장 높은 확률을 가진 클래스 값(=예측 값)을 의미합니다.

조작된 그래프에서도 $\theta^*$'와 $c^*_v$' 값을 구하는 방법은 같습니다.
attacker의 목표는 원래 그래프의 예측 클래스 값인 $c^*_v$와 조작된 클래스 값인 $c^*_v$'가 다른 것입니다.

다시 말하면, 조작된 $c^*_v$'의 예측 (로그)확률값은 최대한 늘리고, 원래의 $c^*_v$의 예측 (로그)확률값은 최대한 낮추는 것입니다.

최종적으로 정리한 objective function은 위와 같습니다.
이 최적화 문제에서 어려운 점은 인접행렬 A'가 이산적이기 때문에 gradient 기반 최적화 방법을 쓸 수 없다는 것입니다. 또한, 조작된 A'와 X'에 대해 GCN은 항상 다시 train되어야 한다는 것입니다. ($\theta^*$'를 새로 계산하기 위해서)

3) how vulnerable GCN is

한줄 요약: 작정하고 속이면 엄청 취약하지만, 아닌 경우에는 어느정도 robust하다.

실험에서 사용한 원래의 그래프는 ground truth label이 class 6이고, confidence가 높은 모델입니다.

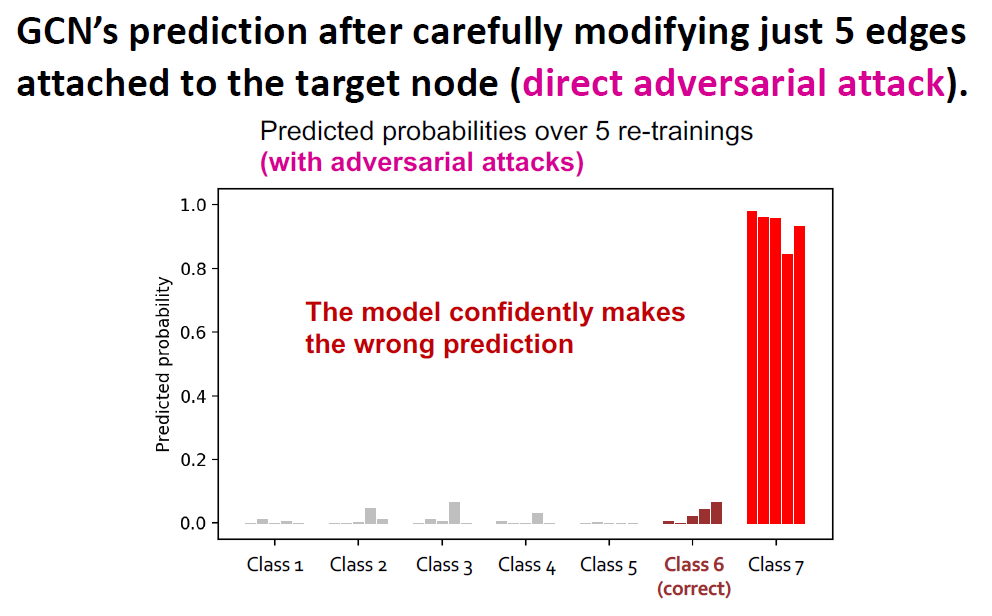
하지만, direct adversarial attack으로 단 5개의 엣지를 추가한 결과 5번의 training 모두에서 class 7로 잘못된 예측을 하게 되었고, confidence는 더 높아졌습니다.

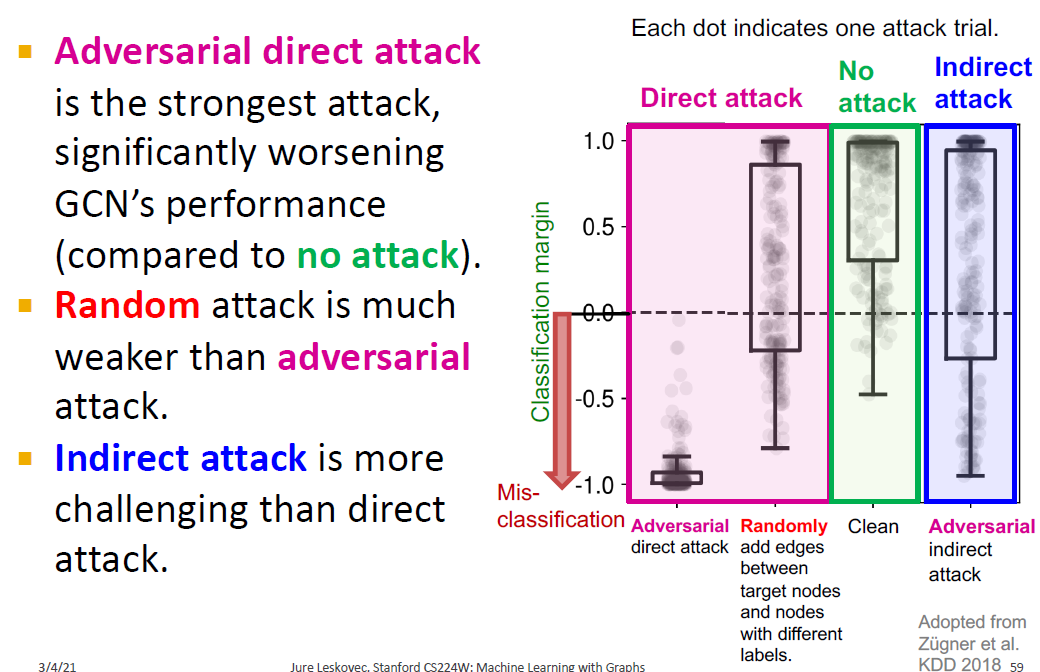
다른 종류의 공격들과 비교를 해보면, direct attack인 경우에는 상당히 취약한 것을 볼 수 있고, random attack이나 indirect attack은 영향이 크지만 direct attack만큼은 아니라는 것을 볼 수 있습니다.