
14기 김상현
Graph Generation
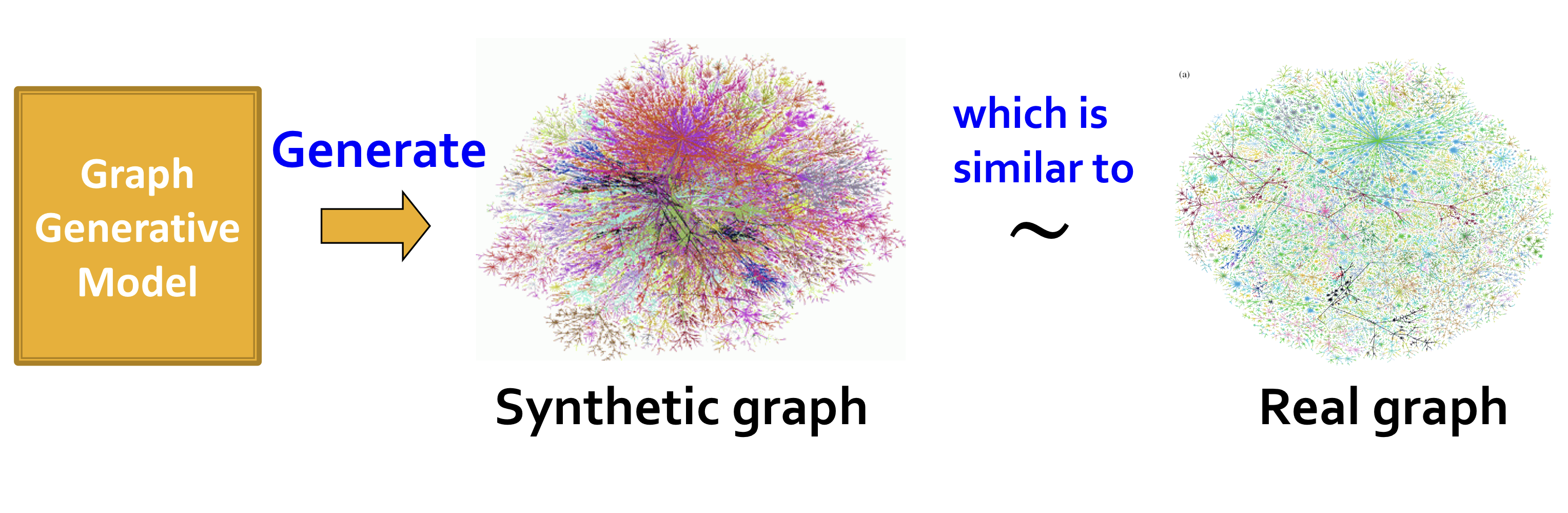
Given
- Graphs sampled from
Goal
- Learn the distribution
- sample from
실제 그래프 분포 샘플들을 이용해 를 학습하고, 학습된 에서 샘플링하여 그래프를 생성한다.
Setup
- is the data distribution, which is never known to us, but we have sampled
- is the model, parametrized by , that we use to approximate
Density Estimation
Make close to
Maximum Likelihood Estimation을 이용한다. 즉, 표본들을 이용해 의 likelihood를 최대로 하는 최적의 parameter 를 찾는다.
Sampling
Sample from
- Sample from a simple noise distribution (e.g. standard normal distribution)
- Transform the noise via
를 deep neural network로 구성하고, 갖고 있는 데이터들을 이용해 학습시킨다.
Auto-regressive models
는 density estimation과 sampling에 사용되고, 이를 위해 auto-regressive model을 사용한다.
Idea: Joint distribution이 conditional distribution들의 곱으로 표현될 수 있는 Chain rule을 이용한다.
이를 위해 를 sequence로 보고, 는 t번째 행동이 된다. 여기서 행동은 node 또는 edge를 추가하는 것이다.
GraphRNN: Generating Realistic Graphs
Model Graph as Sequences
Generating graphs via sequentially adding nodes and edges
node odering 에 따라 Graph 는 node와 edge들의 sequence인 에 유일하게 매핑된다.
Node-level
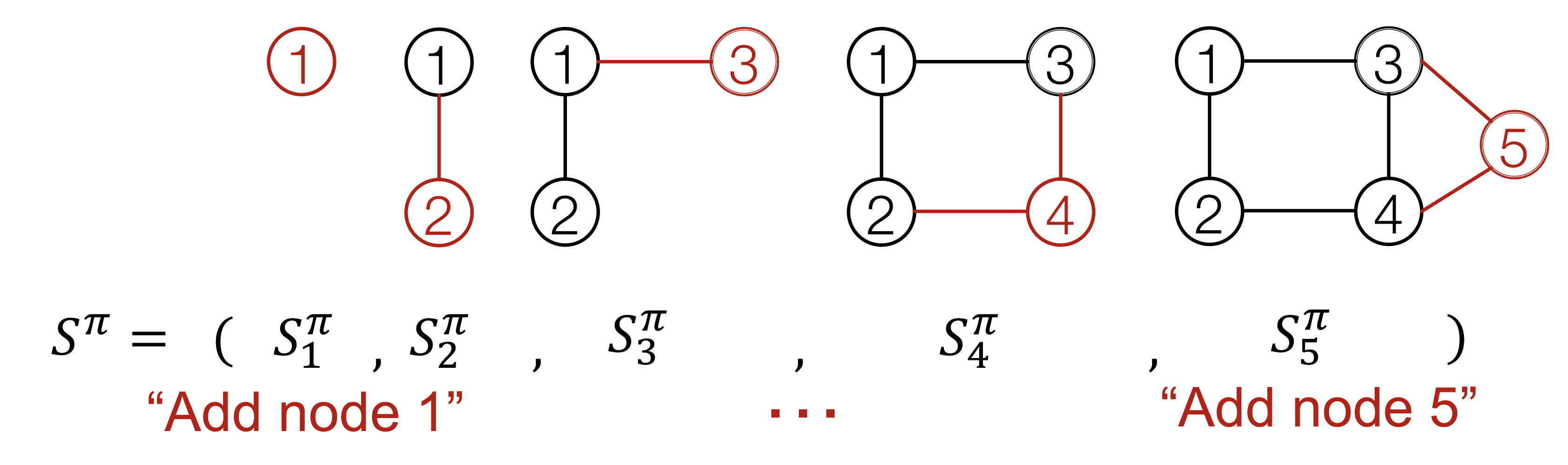
각 단계마다 새로운 노드를 하나씩 추가
Edge-level
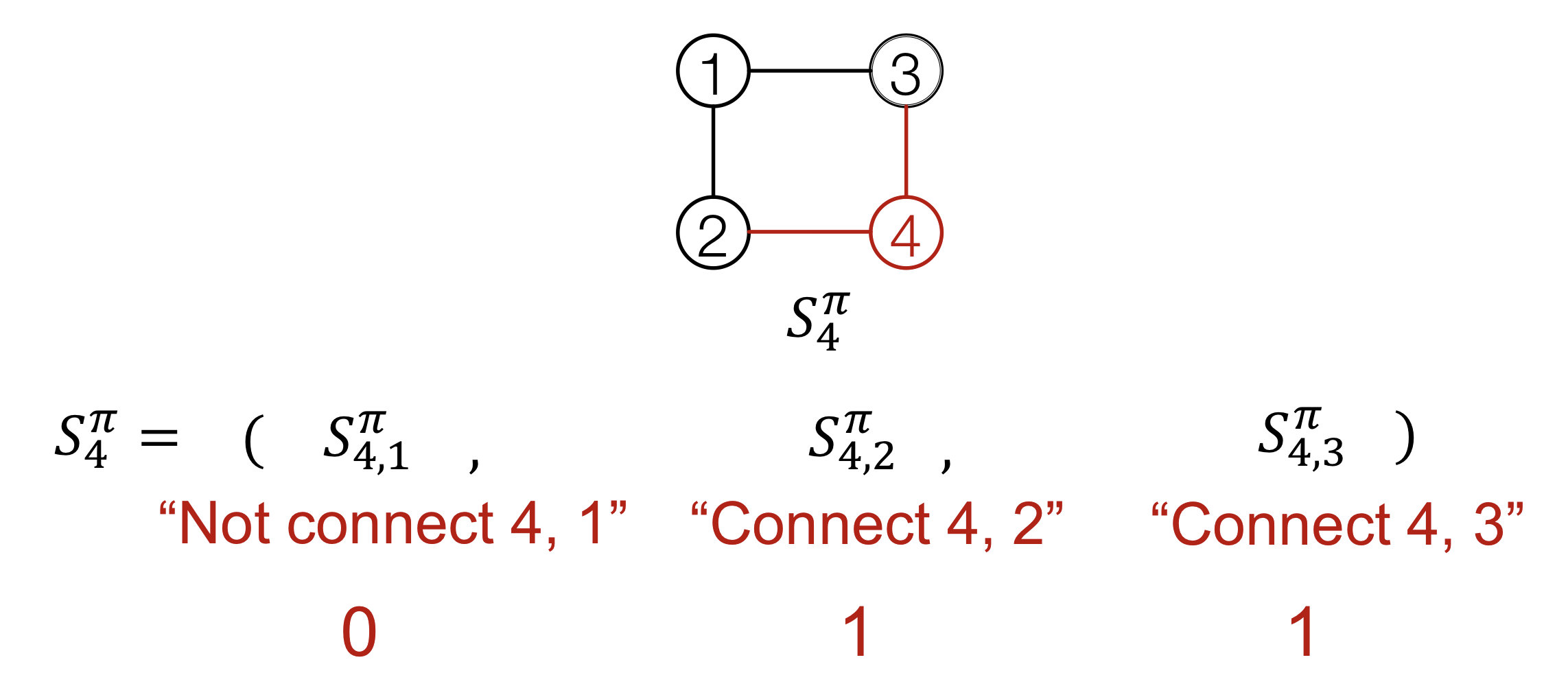
각 단계마다 존재하는 node들 간의 edge들을 추가
각 node-level 단계는 edge-level sequence로 구성된다.
Summary
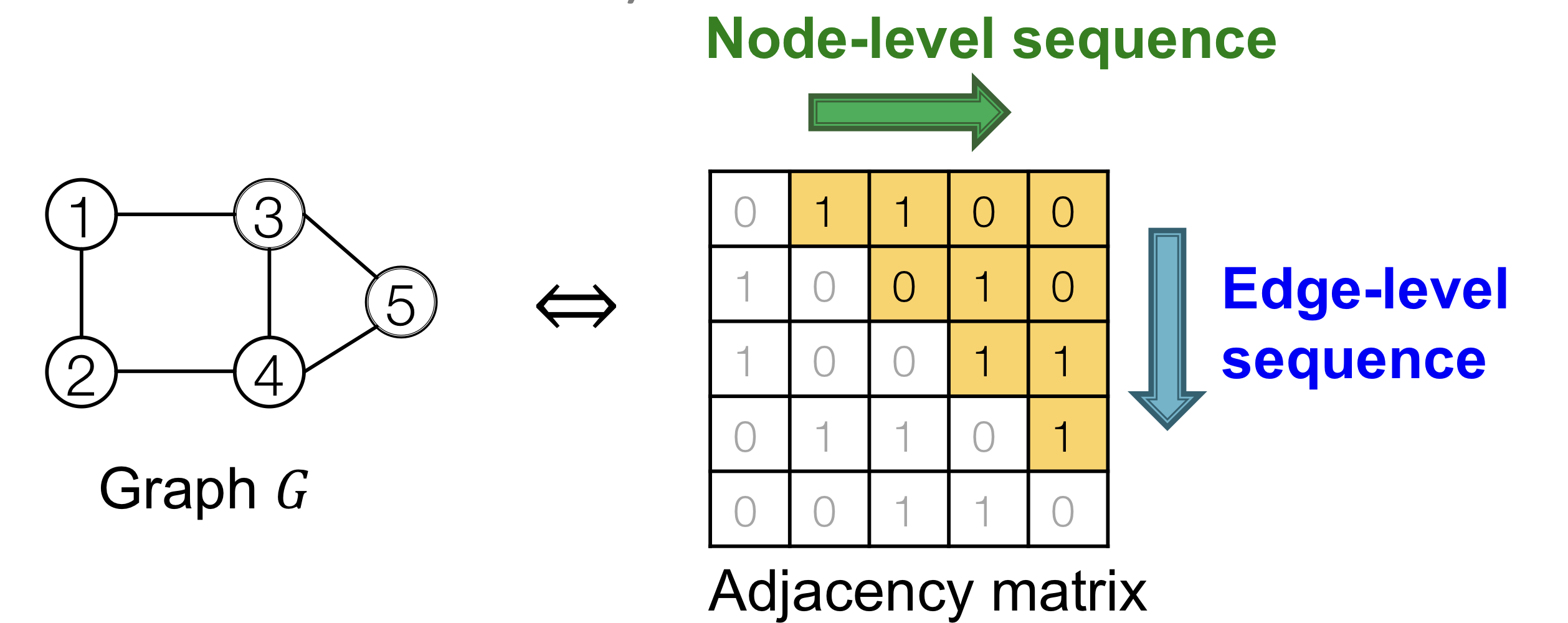
A graph + a node ordering = A sequence of sequences
따라서 graph generation을 sequence generation으로 변형해서 생각한다.
- Node-level sequence: Generate a state for a new node
- Edge-level sequence: Generate edges for the new node based on its state
위의 2개의 과정들을 RNN(Recurrent Neural Networks)를 사용해서 모델링한다.
Background: RNN
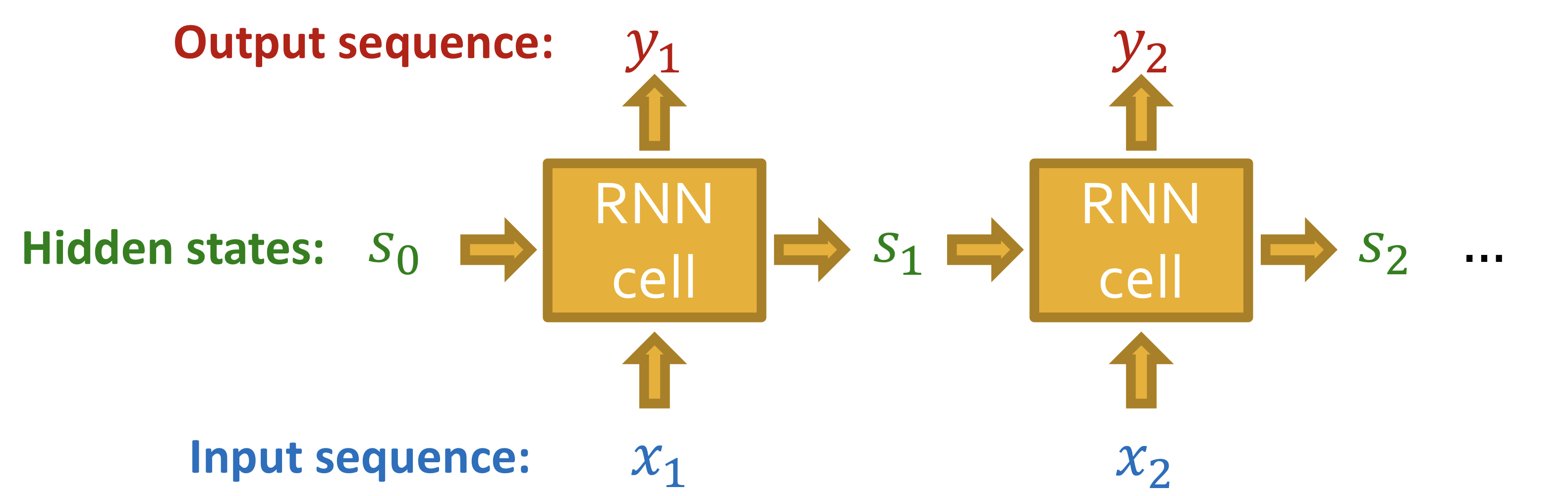
RNN은 sequential data를 위해 고안됐다.
- RNN은 순차적으로 input sequence를 받아 hidden states를 update한다.
- Hidden states는 RNN 입력의 모든 정보를 요약한다.
- Update는 아래 그림의 RNN cells를 통해 수행된다.
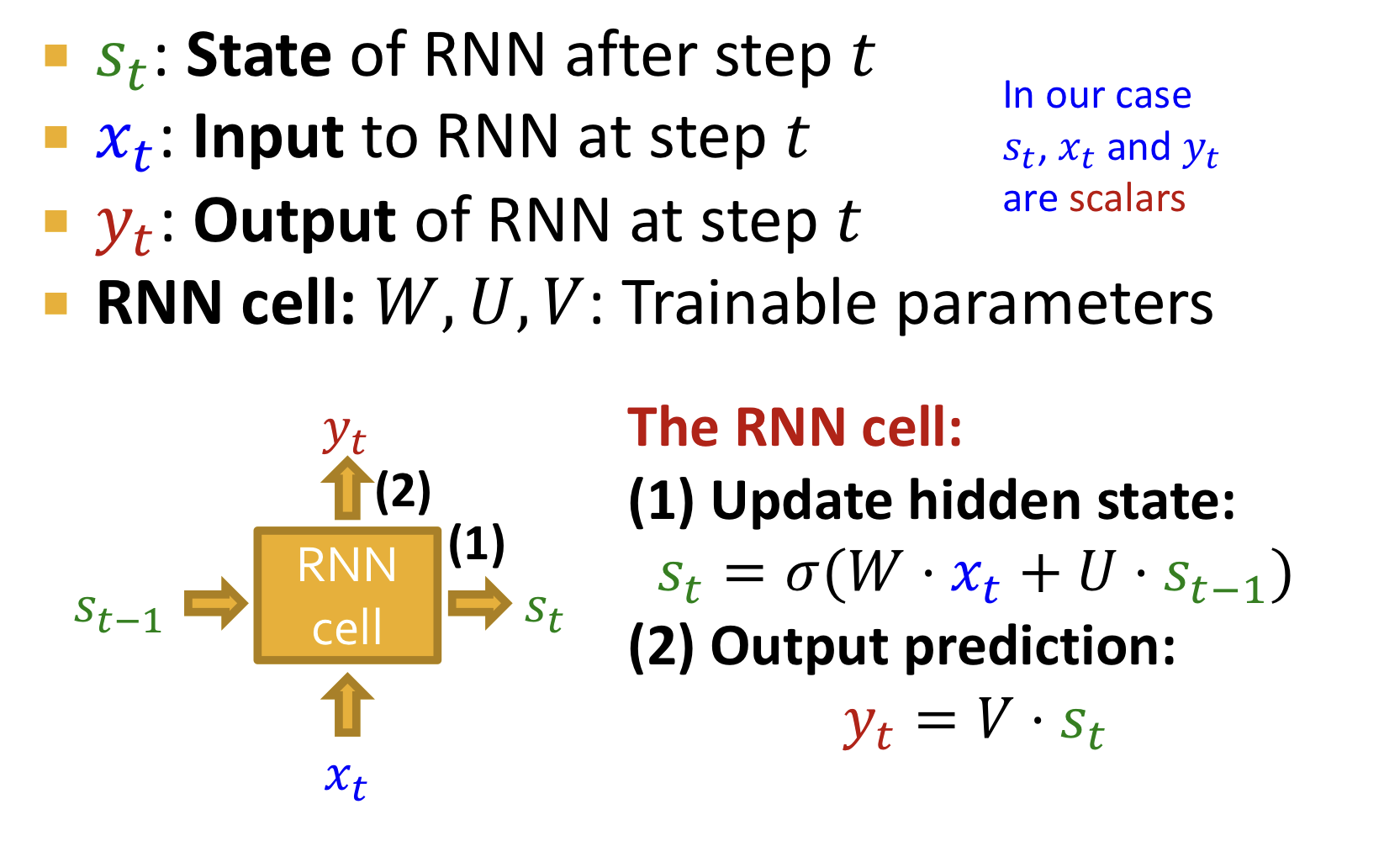
GraphRNN
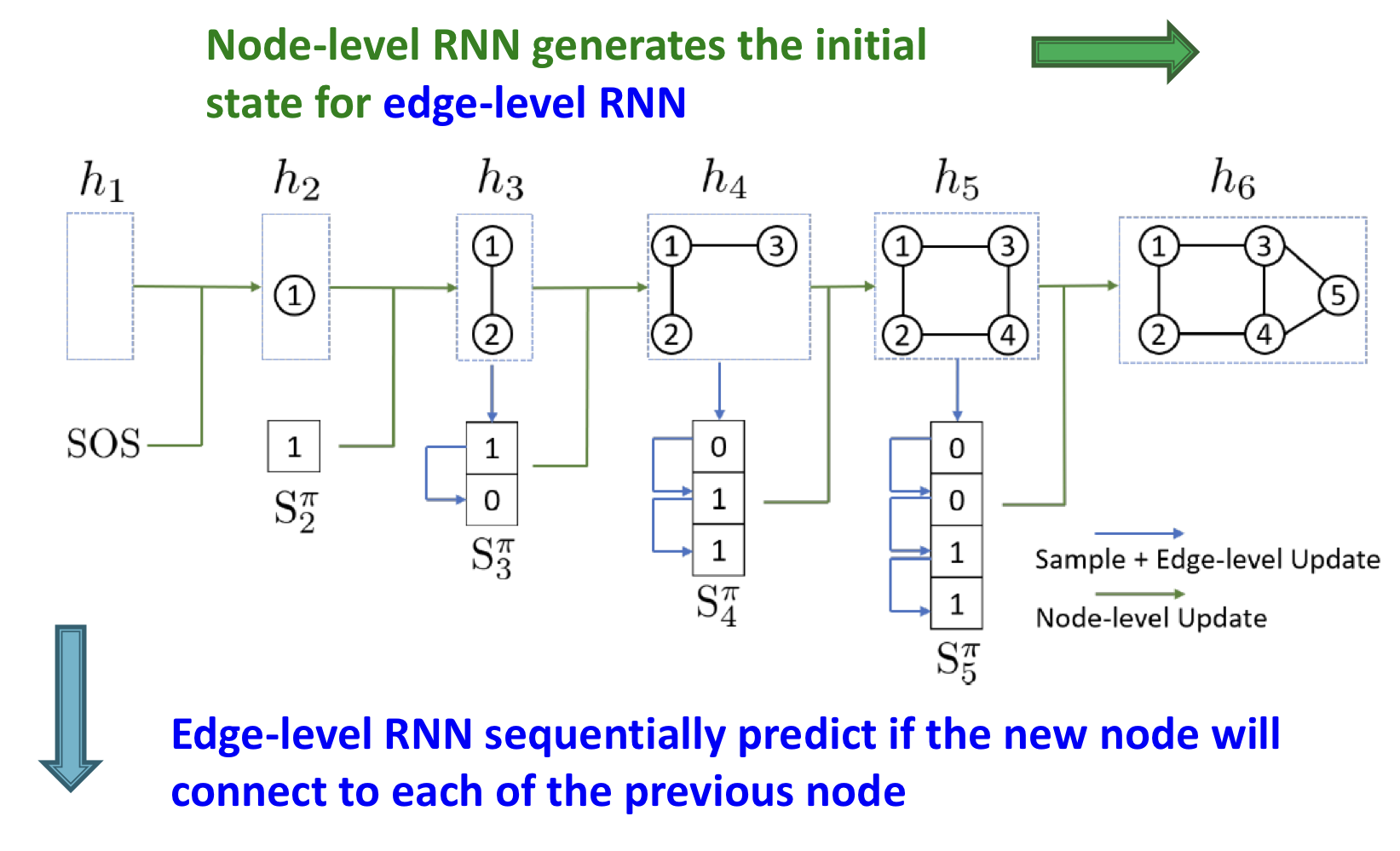
GraphRNN은 node-level RNN과 edge-level RNN을 갖는다.
Relationship between the two RNNS
- Node-level RNN generates the initial state for edge-level RNN
- Edge-level RNN sequentially predict if the new node will connect to each of the previous node
RNN for Sequence Generation
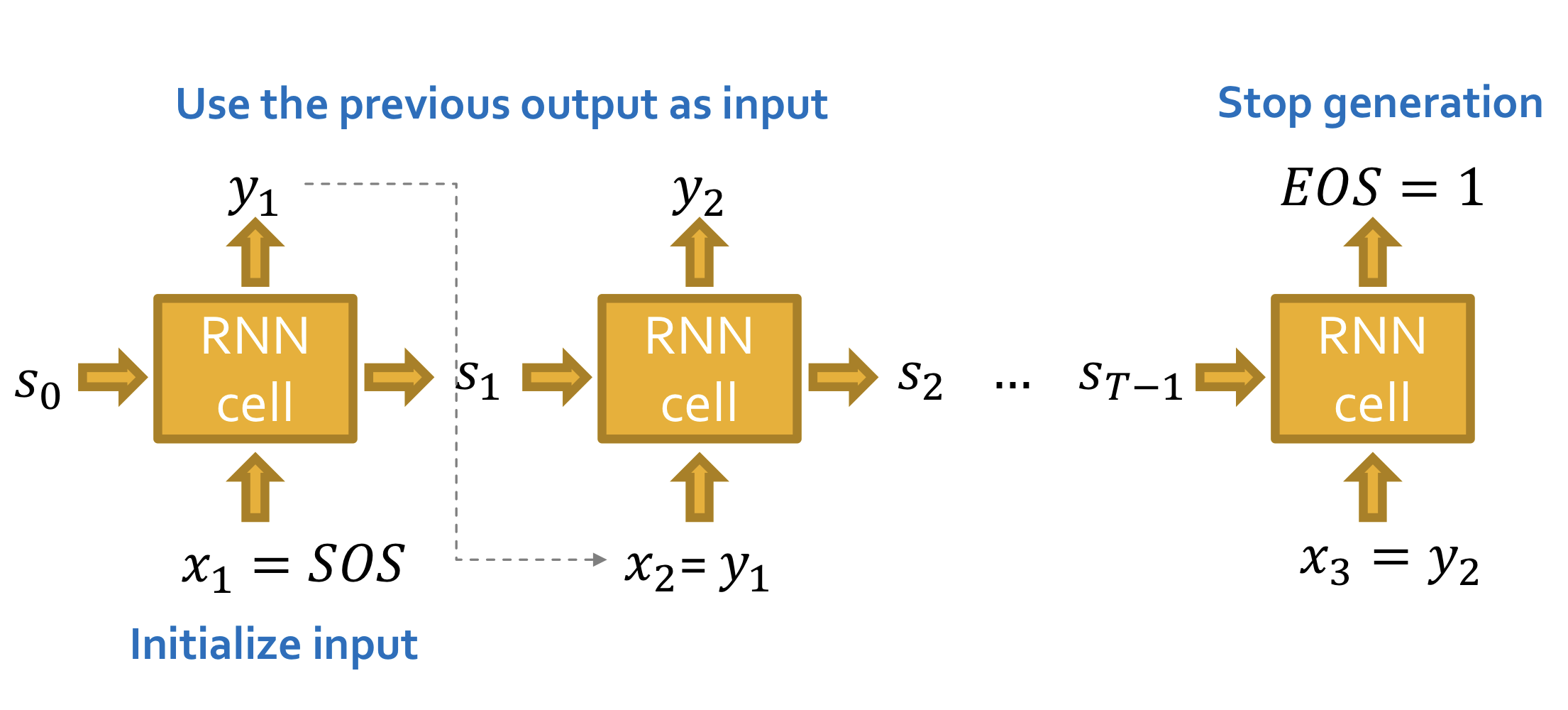
- 이전 출력(previous output)를 입력으로 사용해서 sequence를 생성
- Start of sequence token(SOS)를 초기(initial) 입력으로 사용
- End of sequence token(EOS)를 RNN의 추가 출력으로 사용해서 생성을 멈춤
이와 같이 생성할 경우 결정론적(deteministic)인 모델이 된다.
Our goal: Use RNN to model
라 하자. 그러면 를 에서 샘플링 해야한다. 즉,
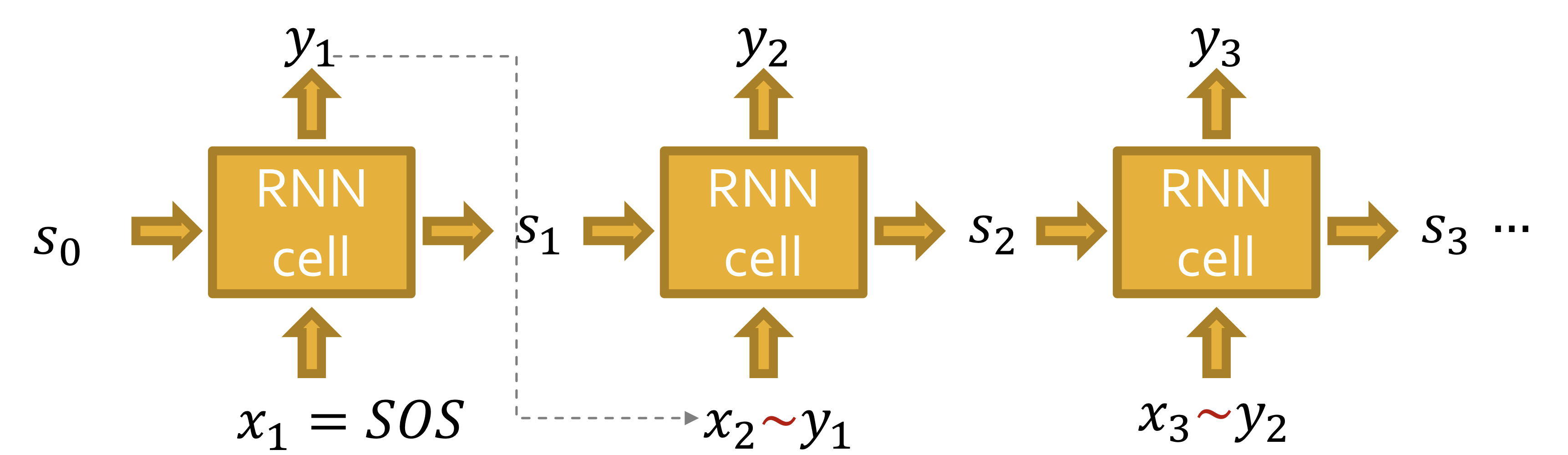
- RNN은 각 단계에서 확률을 출력
- 확률 분포에서 샘플링하고, 다음 단계의 입력으로 사용
Test Time
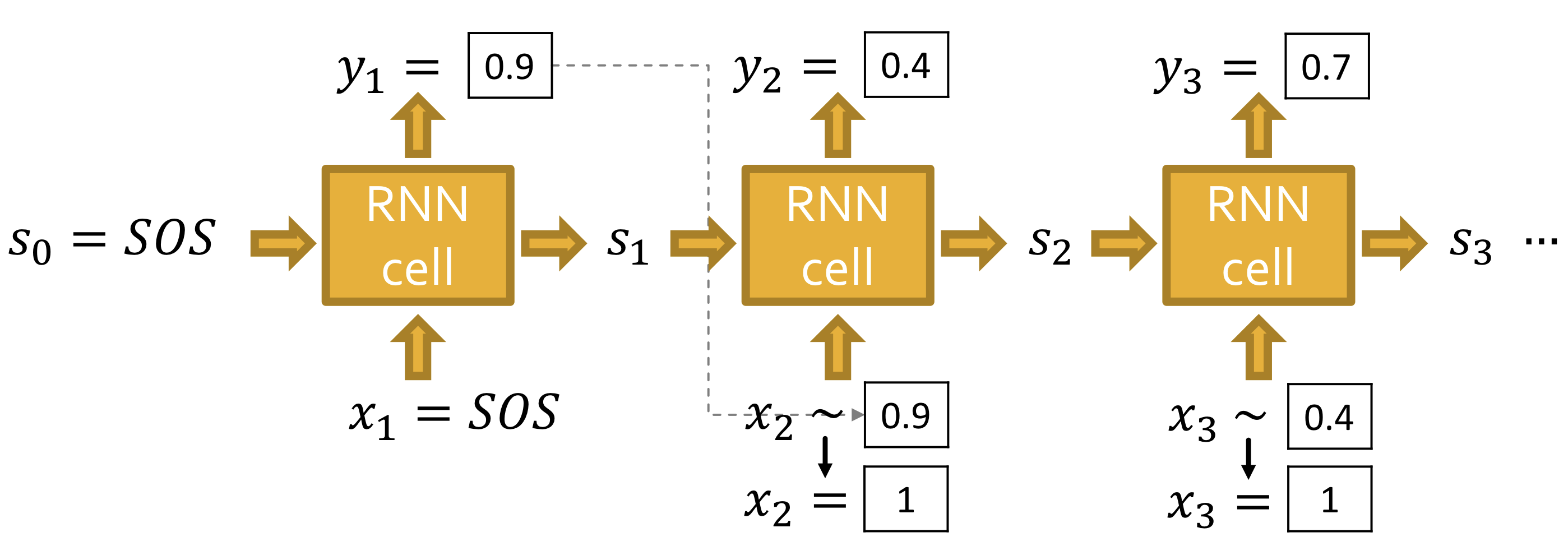
이미 학습된 모델을 갖고 있다고 가정하자
- 는 베르누이 분포를 따르는 scalar
- 의 확률에 따라 을 샘플링해서 다음 단계의 입력으로 사용
Traning time
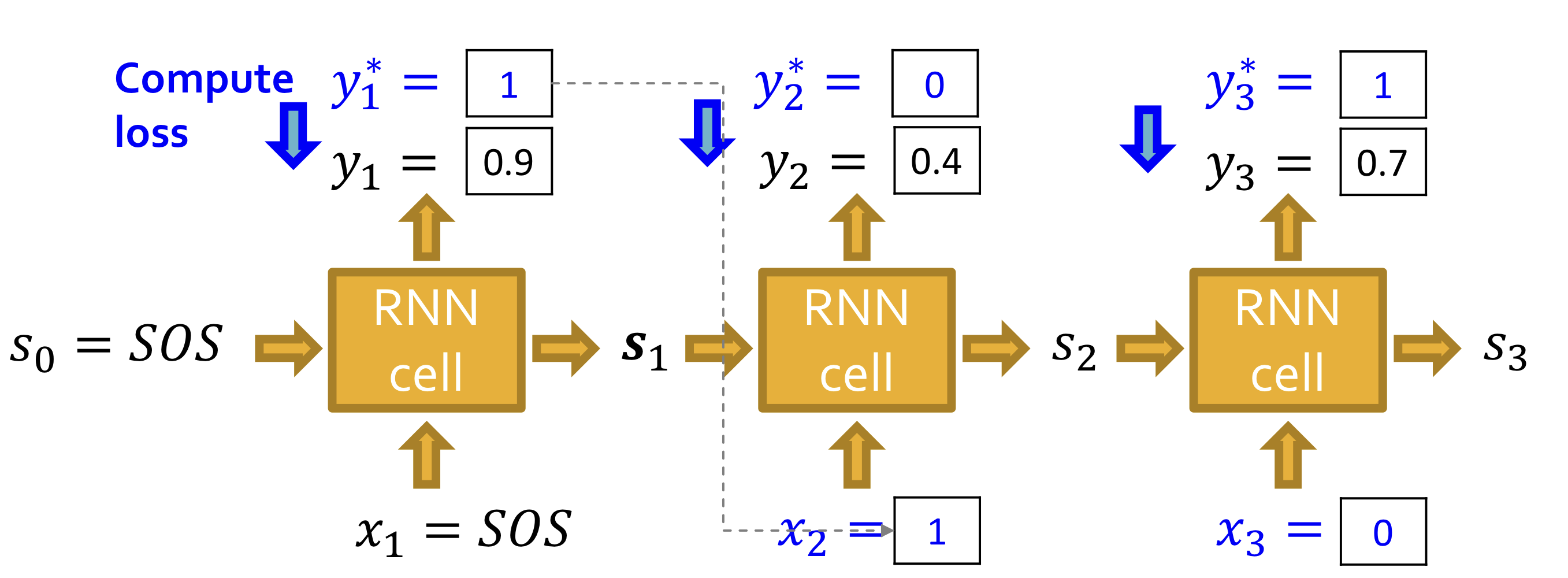
위의 그림과 같이 ground truth 와 prediction 를 비교해 loss를 계산하고, teacher forcing을 이용해 다음 단계 입력으로 ground truth를 사용한다.
Teacher Forcing(교사 강요)
훈련 과정에서는 이전 시점의 디코더 셀의 출력을 현재 시점의 디코더 셀의 입력으로 넣어주지 않고, 이전 시점의 실제값을 현재 시점의 디코더 셀의 입력값으로 하는 방법을 사용할 겁니다. 그 이유는 이전 시점의 디코더 셀의 예측이 틀렸는데 이를 현재 시점의 디코더 셀의 입력으로 사용하면 현재 시점의 디코더 셀의 예측도 잘못될 가능성이 높고 이는 연쇄 작용으로 디코더 전체의 예측을 어렵게 합니다. 이런 상황이 반복되면 훈련 시간이 느려집니다. 만약 이 상황을 원하지 않는다면 이전 시점의 디코더 셀의 예측값 대신 실제값을 현재 시점의 디코더 셀의 입력으로 사용하는 방법을 사용할 수 있습니다. 이와 같이 RNN의 모든 시점에 대해서 이전 시점의 예측값 대신 실제값을 입력으로 주는 방법을 교사 강요라고 합니다.
참조:https://wikidocs.net/24996
Binary cross entropy를 통해 loss를 계산하고, back propagation을 통해 RNN 모델의 parameter를 update한다.
Putting Things Together
Our plans
- Add a new node: Node RNN을 실행하고, Node RNN의 출력을 Edge RNN의 초기치로 사용
- Add new edges for the new node: Edge RNN을 실행하여 새로운 node가 이전의 node 각각과 연결되는지 예측
- Add another new node: Edge RNN의 마지막 hiddent state를 사용해서 Node RNN을 실행
- Stop graph generation: Edge RNN이 EOS를 출력하면 그래프 생성을 종료
Training
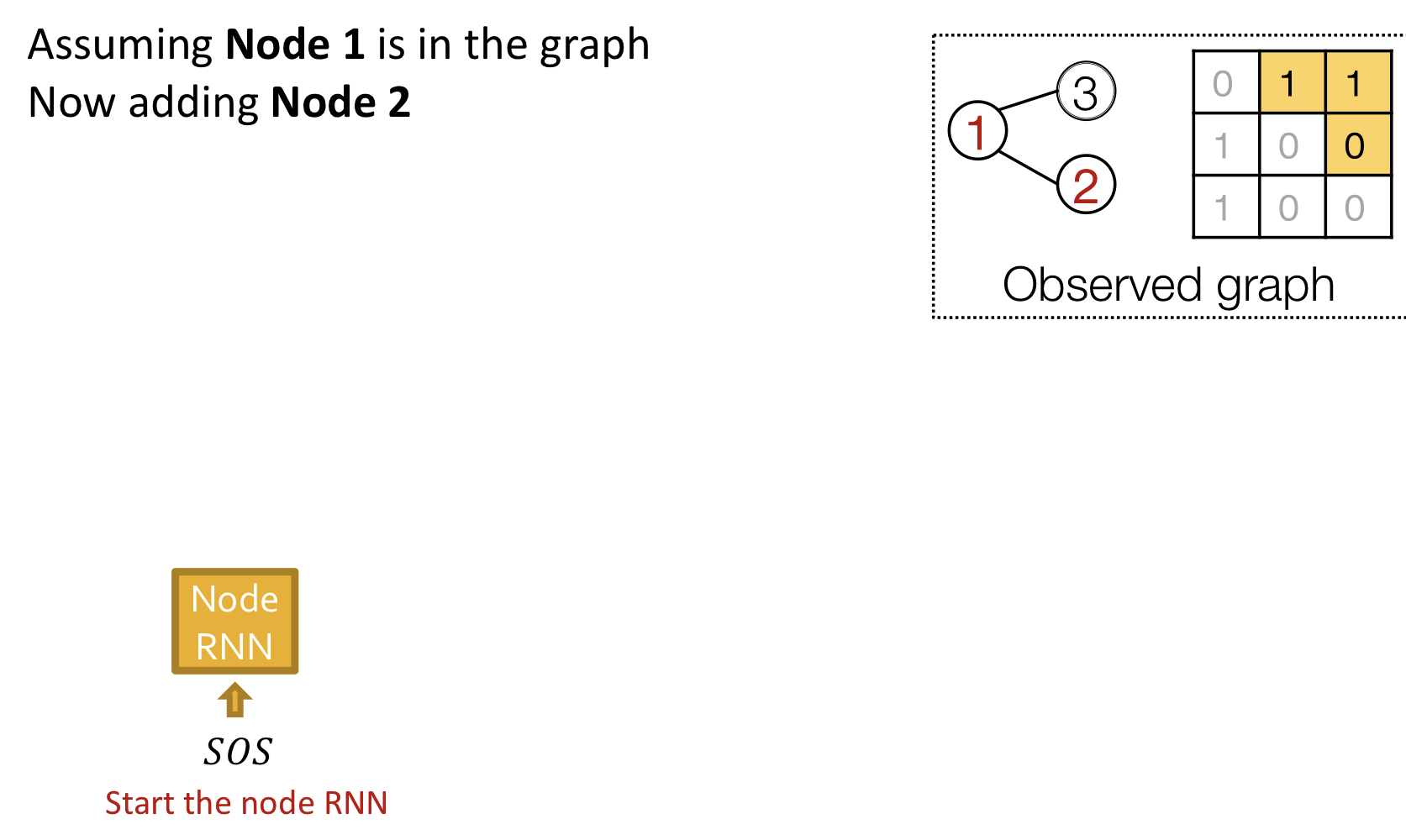
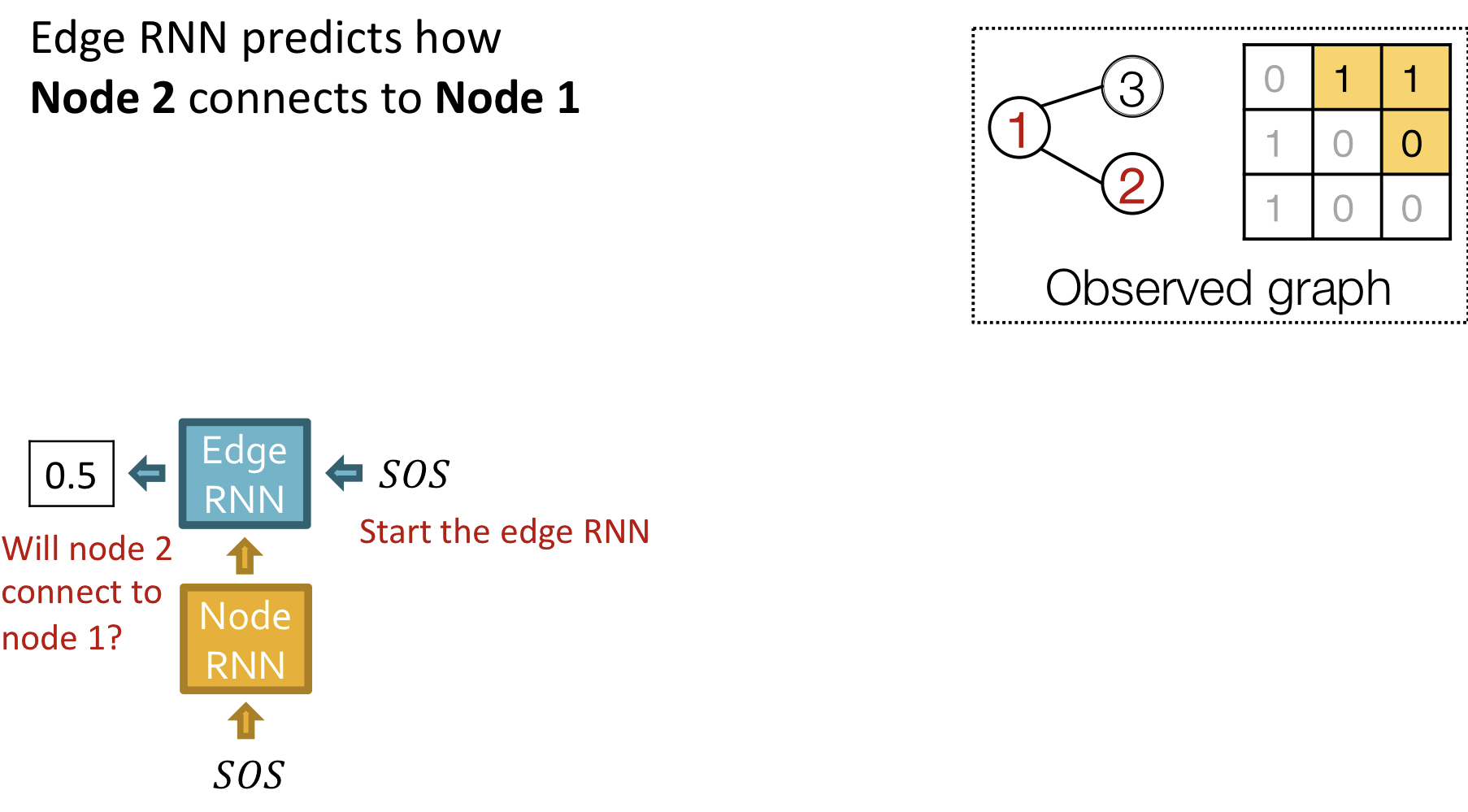
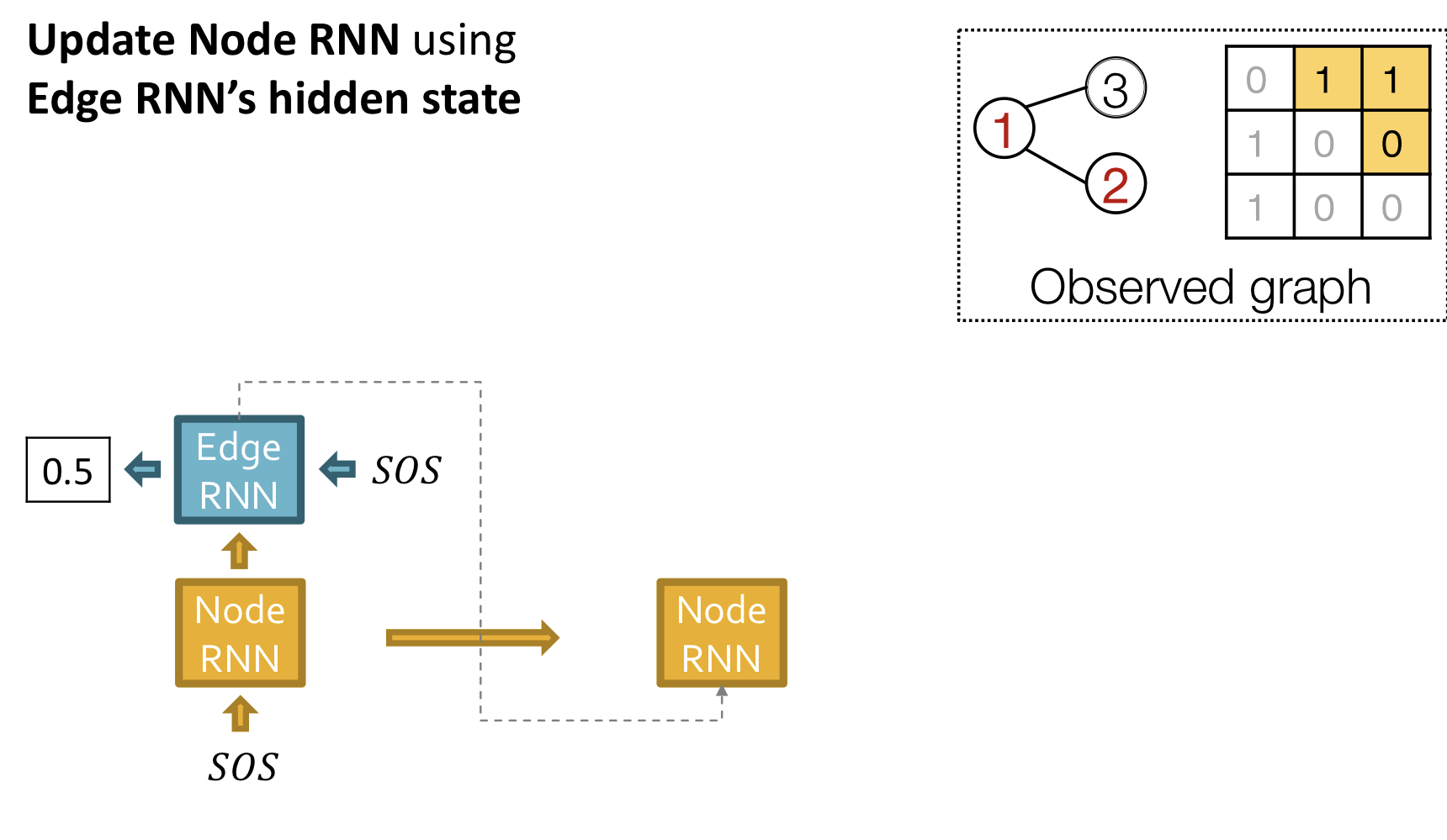
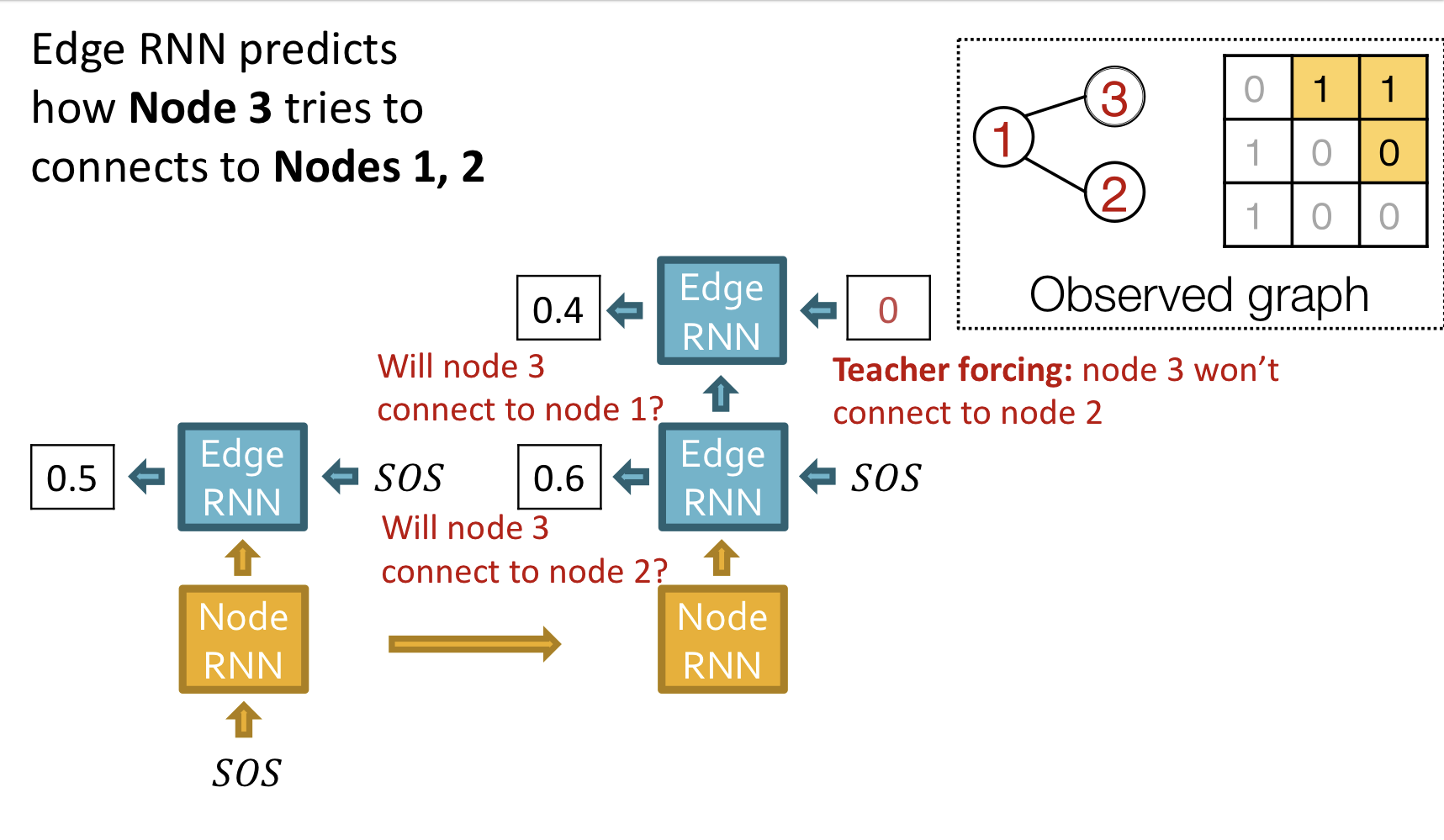
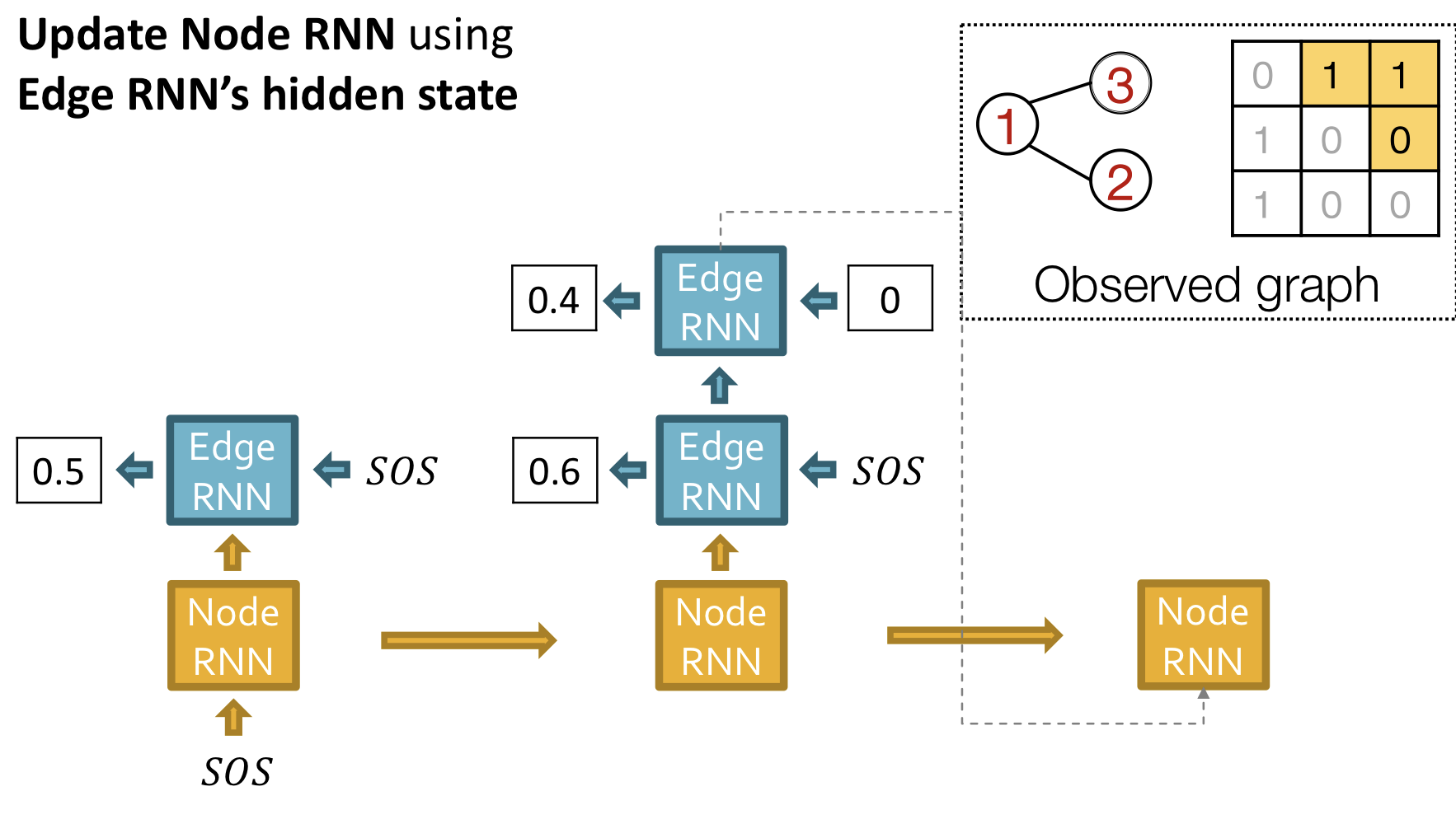
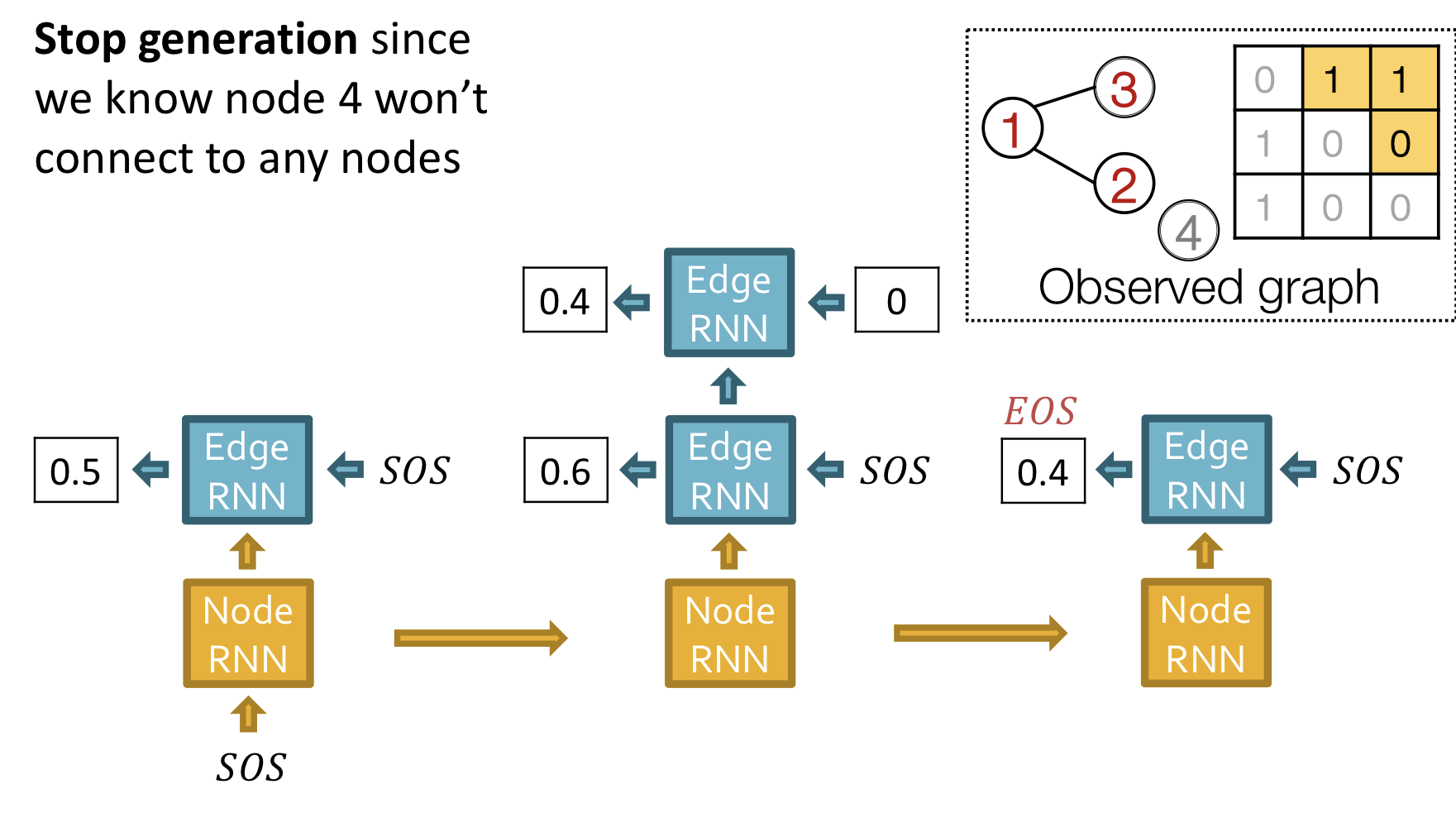
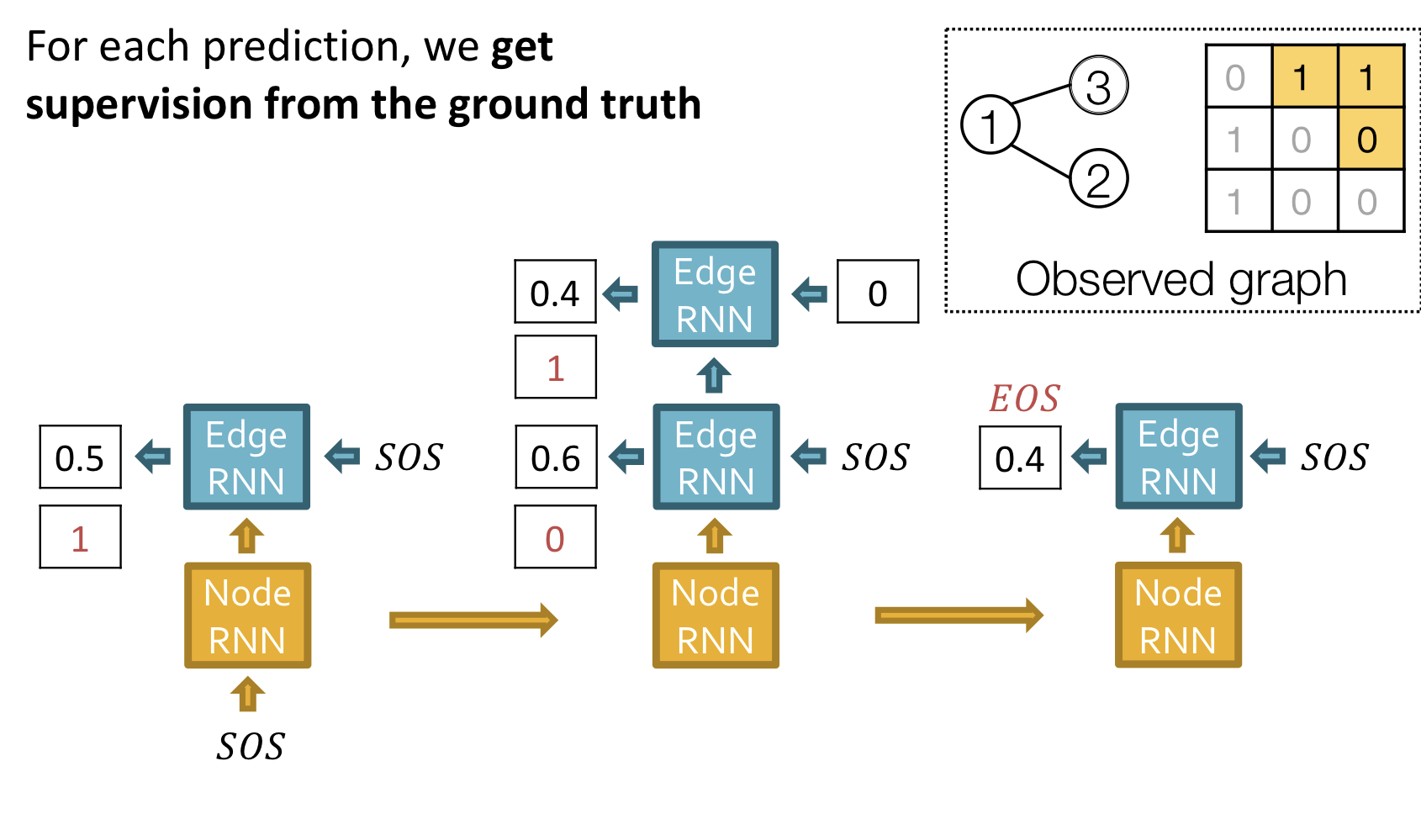
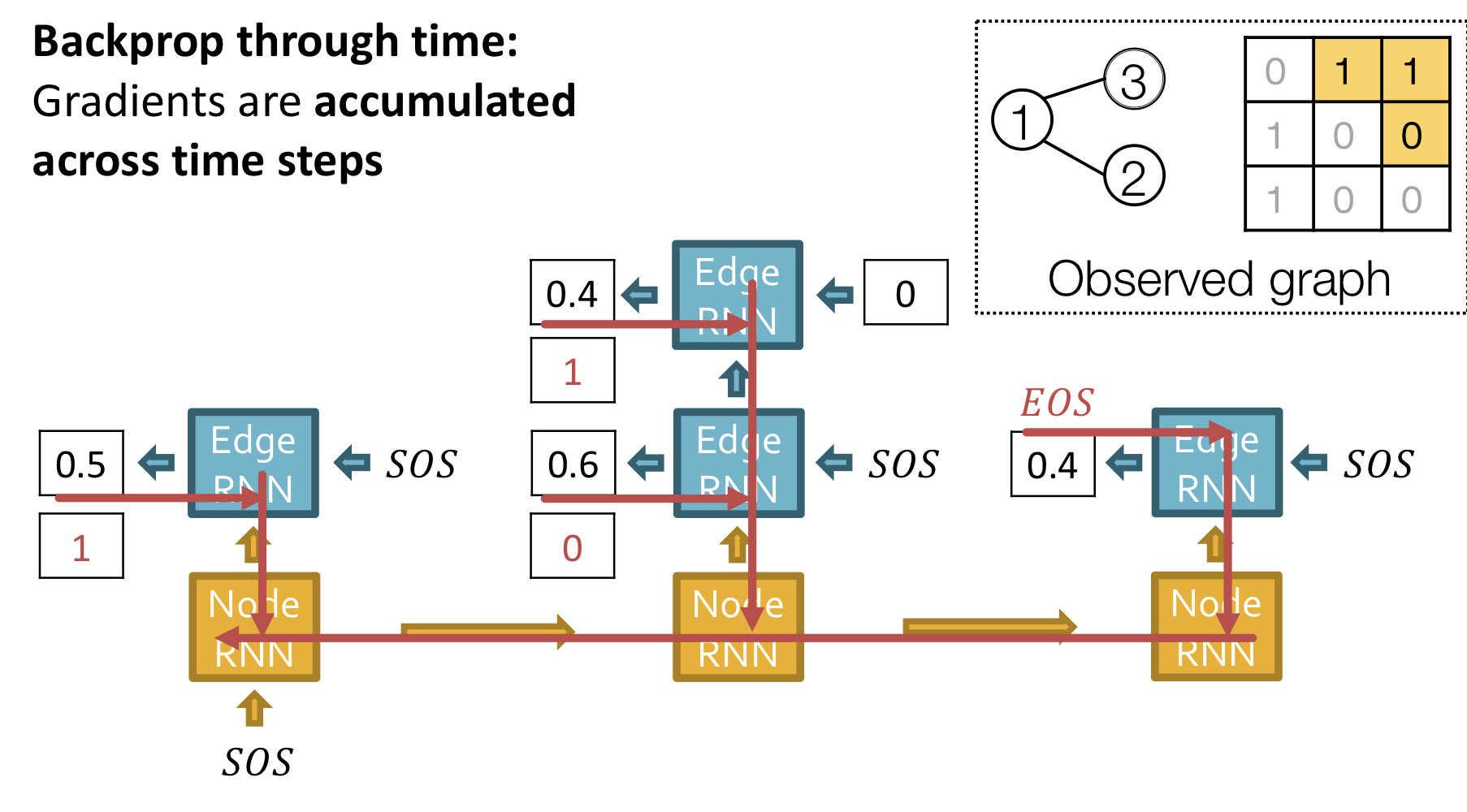
Test
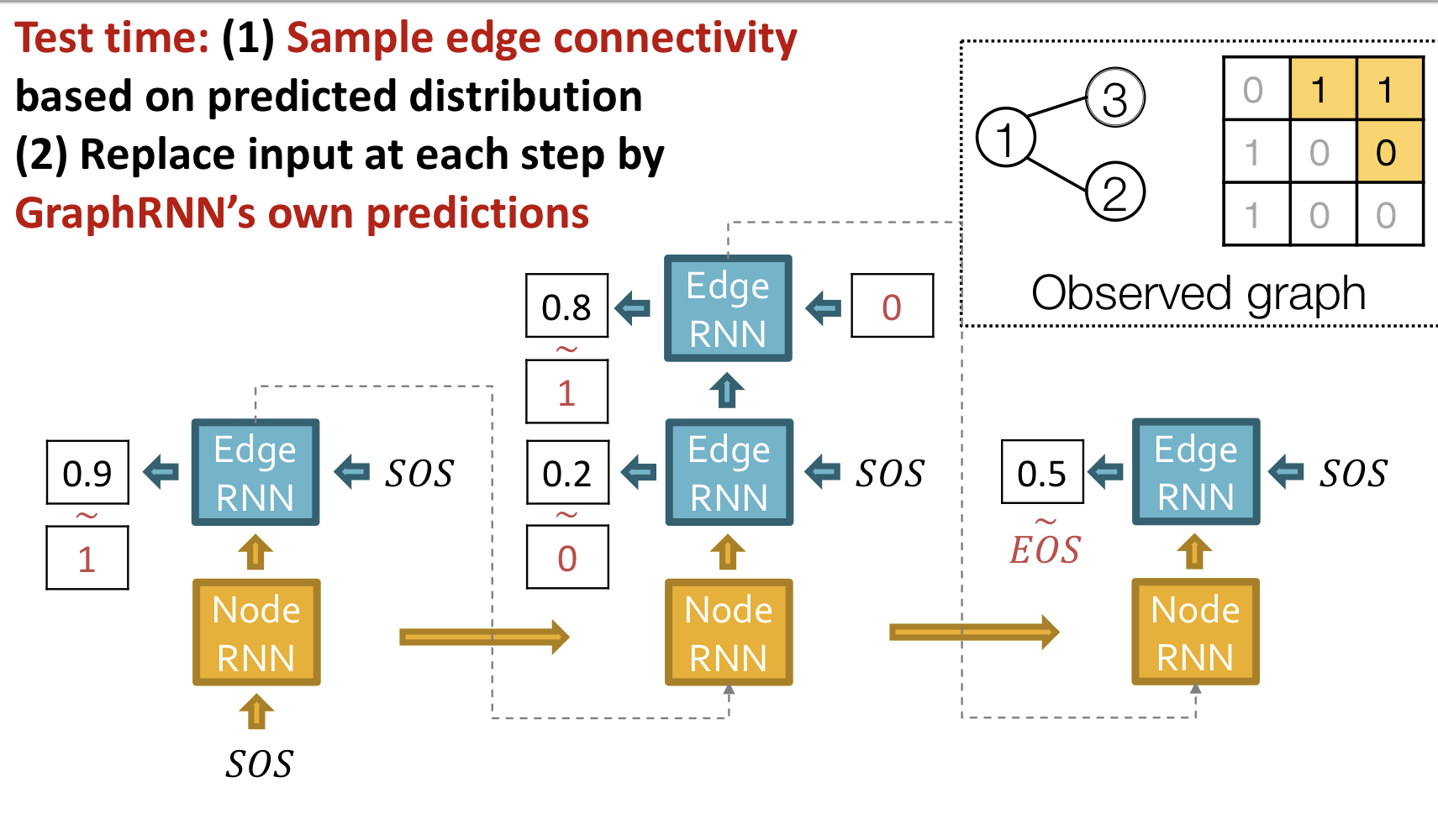
Tractability
Random node ordering의 경우 edge generation시 이전의 모든 노드들을 고려해야해서 복잡도가 증가하고, long-term dependency 문제가 발생한다. 이를 해결하기 위해 BFS(Breadth-First Search) node ordering을 사용한다.
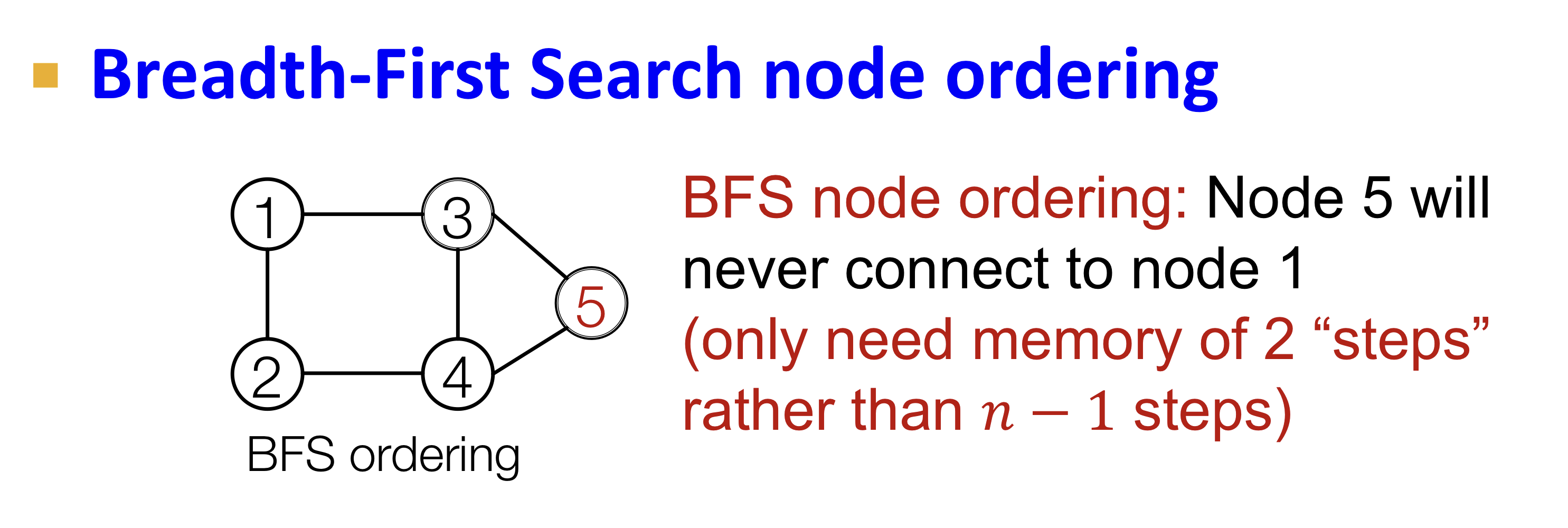
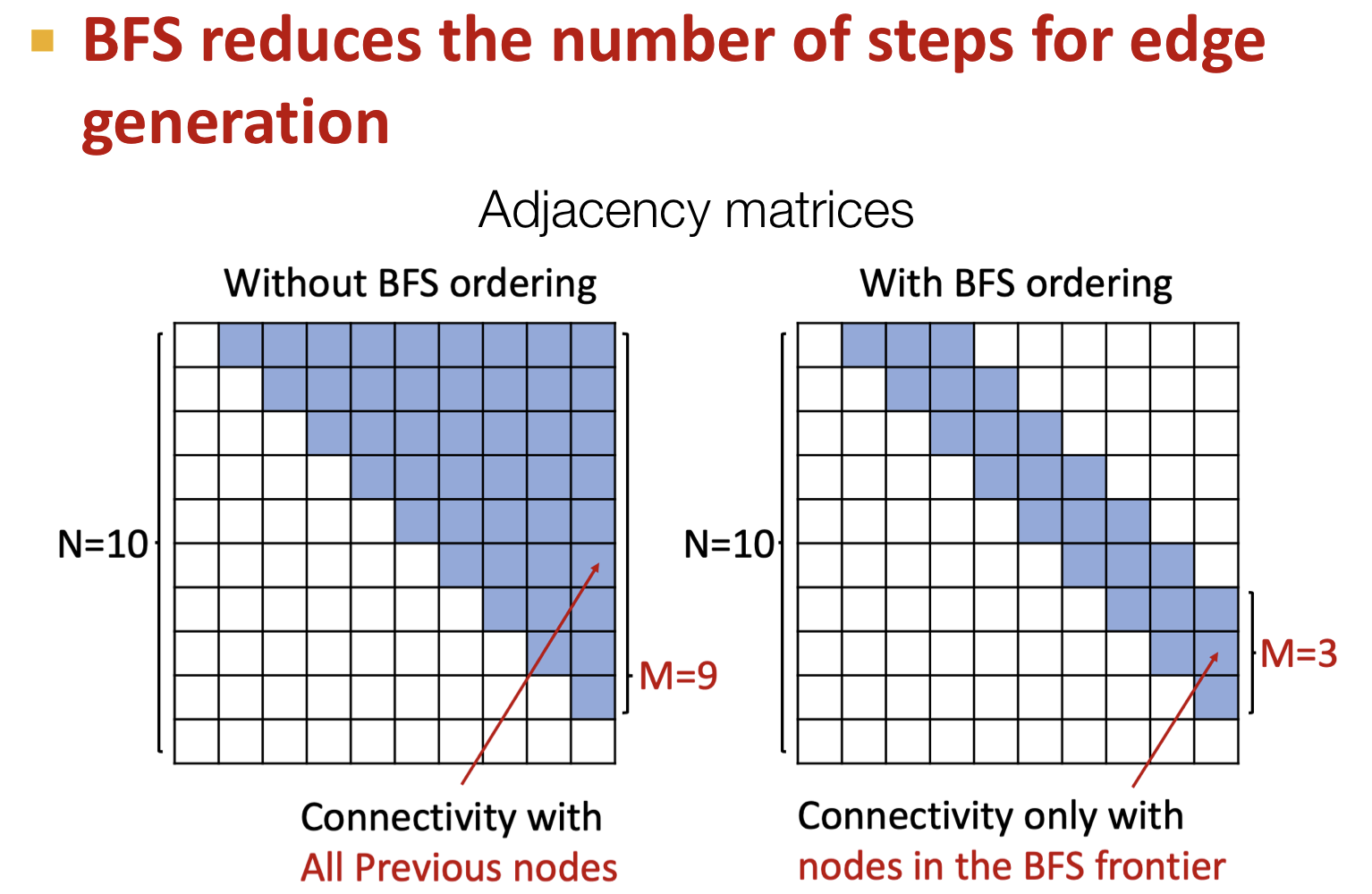
너비 우선 탐색 방법으로 인접한 노드들에 따라 node ordering을 진행한다. 이와 같은 방법은 다음 2가지의 이점이 있다.
- Reduce possible node orderings: node ordering 방법의 경우의 수가 줄어든다. 왜냐하면 random ordering의 경우 이지만, BFS의 경우 이보다 적은 node ordering 경우의 수를 갖는다.
- Reduce steps for edge generation: edge 생성시 인접 노드들과의 관계만 고려할 수 있어 long-term dependency 문제를 해결한다.
Evaluating Generated Graphs

- Visual similarity
- Graph statistics similarity
Visual similarity
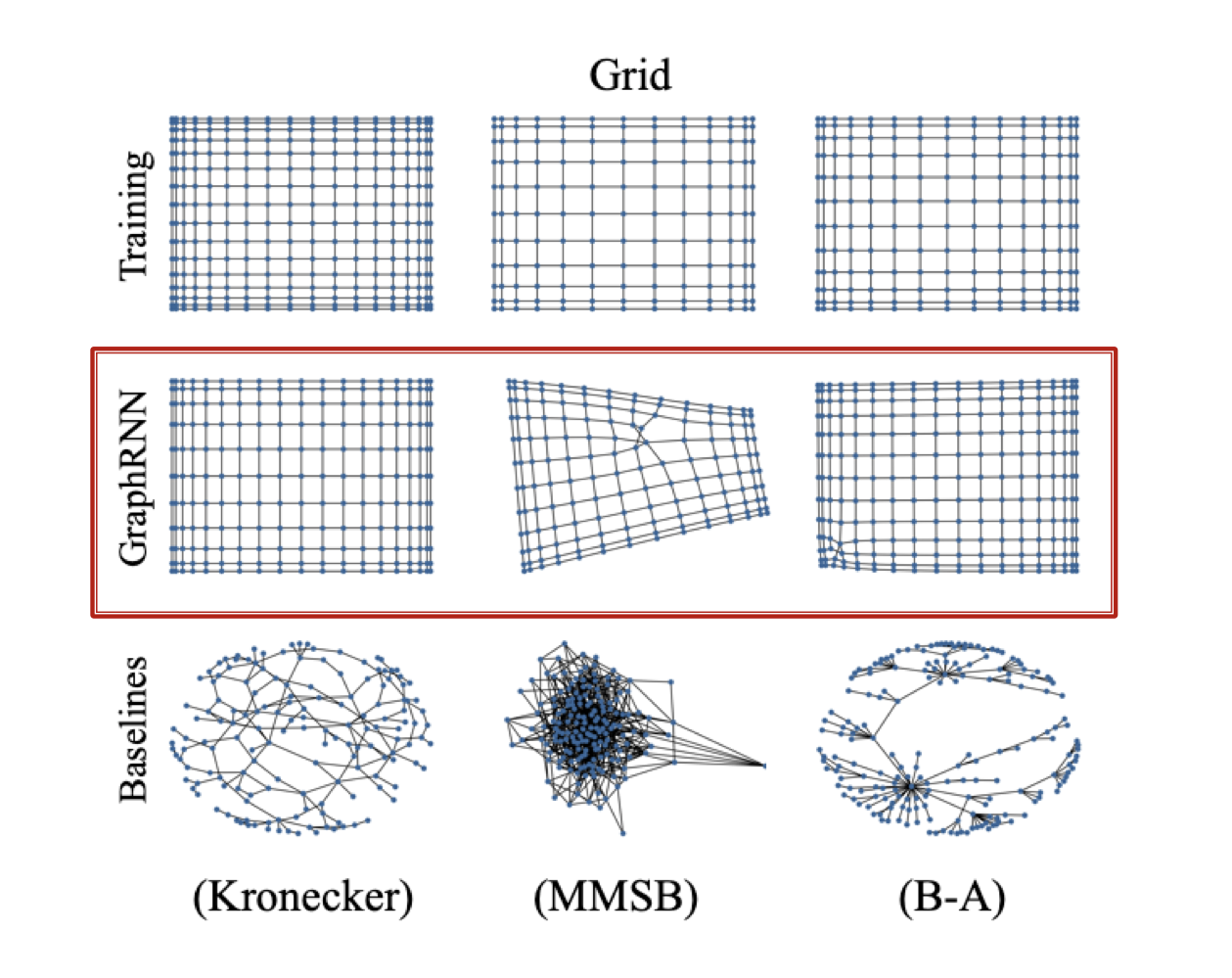
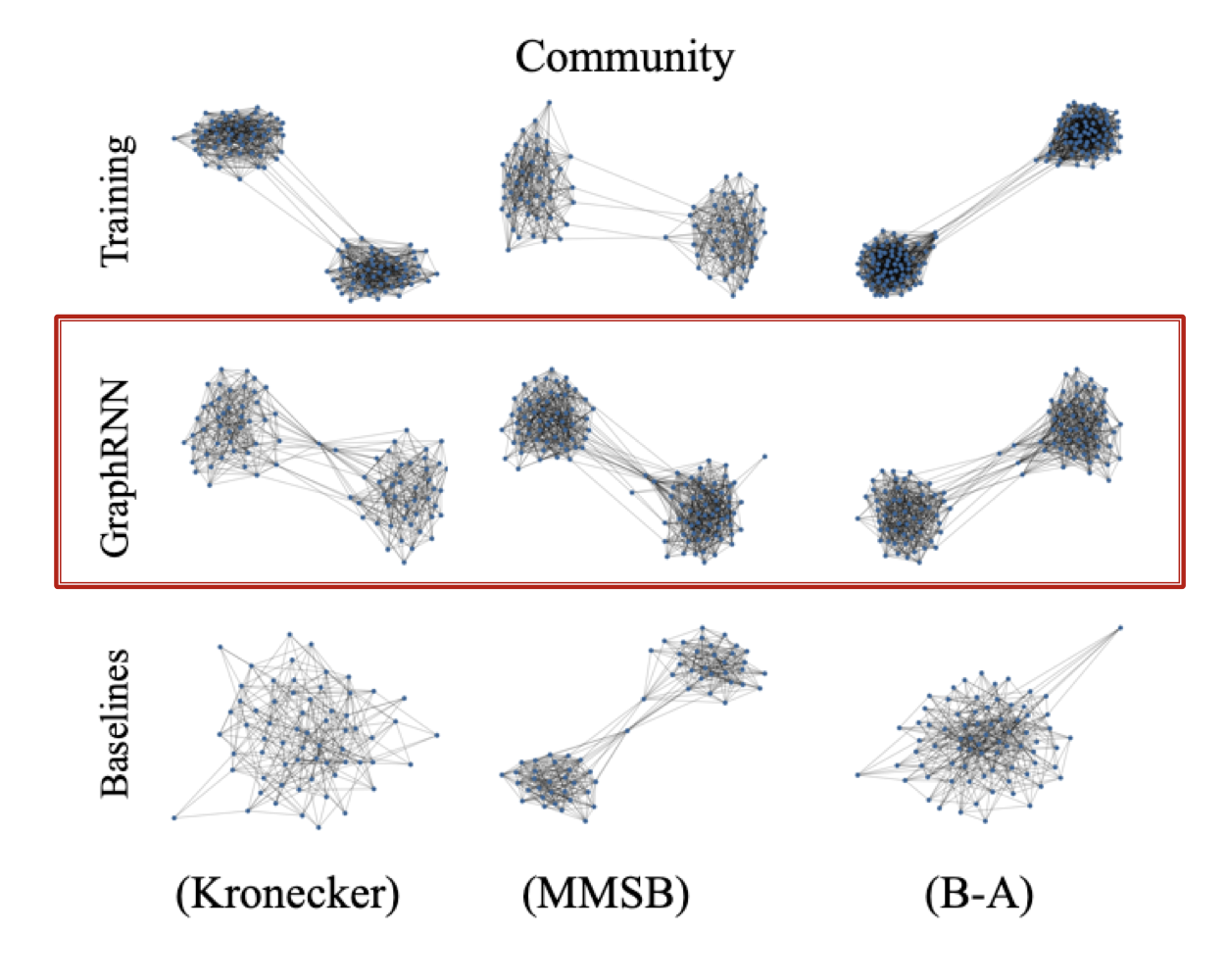
시각화 했을 때, GraphRNN을 통해 생성된 그래프가 실제 그래프와 더 유사한 것을 확인할 수 있다.
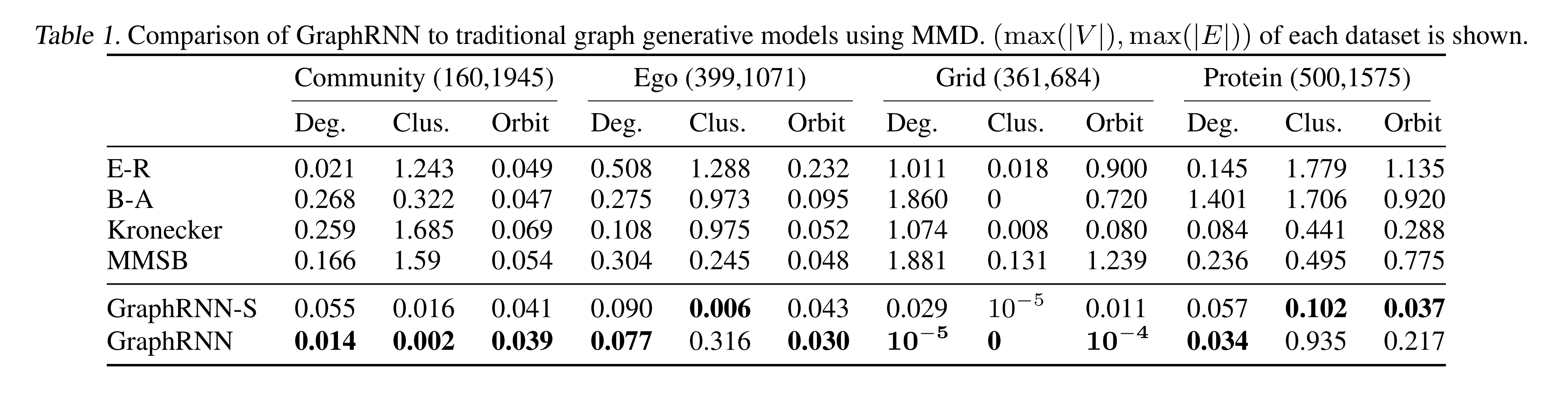
Graph Statistics similarity
시각적으로 유사성을 파악하는 문제는 어렵기 때문에 정량적으로 유사성을 파악하기 위해 그래프 통계치(graph statistics)를 이용해 비교한다.
Typical Graph Statistics
- Degree distribution
- Clustering coefficient distribution
- Orbit count statistics
Training graph statistics 집합과 generated graph statistics를 비교하기 위해 EMD(Earth Mover Distance)와 MMD(Maximum Mean Discrepancy)를 사용한다.
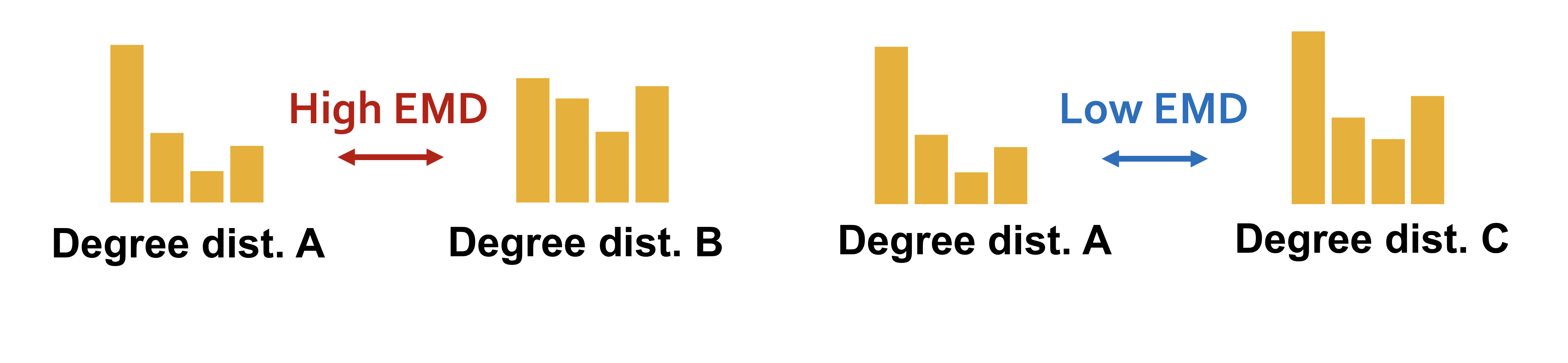
: two distribution
: the set of all distributions whose marginals are p and q respectively
: valid transport plan
EMD는 두 분포의 거리를 측정하는 지표로 하나의 분포에서 다른 분포로 이동할 때 드는 힘(노력)의 최소값을 측정한다. 이때, transport plan에 따라 측정되는 각각의 이동시키는 힘(노력)이 다르기 때문에 이를 최소로 하는 transport plan에 따라 이동시켰을 때 드는 힘(노력)의 기대값을 EMD로 정의한다. 참고로 Earth Mover Distance는 1-Wasserstein Distance와 같다.
Transport plan을 직관적으로 이해하자면 위의 그림에서 A 분포와 B 분포가 존재할 때, A 분포를 이산화(블록 단위로 쪼개는 행위)를 하면 이 되고, B 분포도 마찬가지로 이산화 하면 이 된다. 이때, 블록 와 를 매칭시키는 방법을 tranport plan이라 할 수 있고, 이렇게 매칭된 방법에 따라 블록을 이동시켜 그 때 들어가는 힘(노력)을 계산한 것이 EMD 이다.
참고) 위의 EMD에 대한 설명은 직관적인 이해를 위한 설명입니다.
: kernel function
MMD의 정의는 위의 수식과 같다.
우리는 kernel function으로 EMD를 사용해서 training graph statistics 집합과 generated graph statistics 집합을 비교한다.
즉, 수식에서 는 training graph statistics 집합 분포이고, 는 generated graph statistics 집합 분포이다.
Application of Deep Graph Generative Models
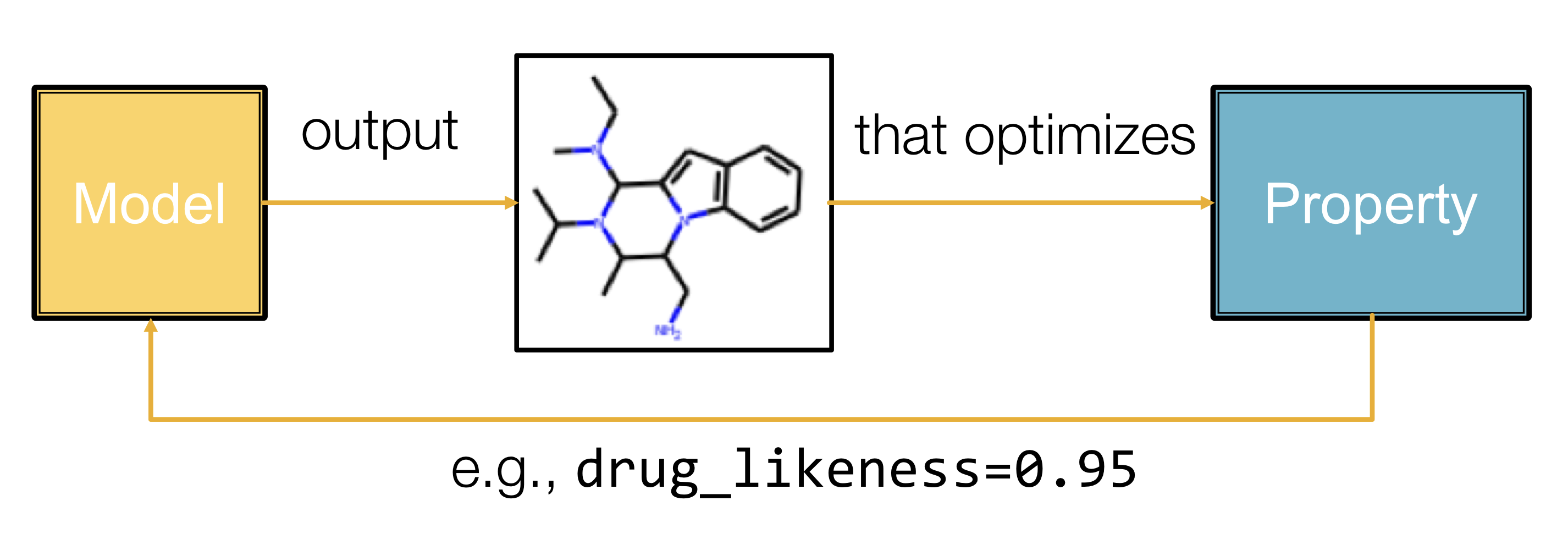
그래프 생성 모델을 사용해 신약 개발(drug discovery)에 활용할 수 있다. 이를 위해서는 다음 조건을 만족해야 한다.
- Optimize a given objective (high scores): 약과 같은 특성을 갖게 최적화 되어야 한다.
- Obey underlying rules (valid): 타당한 화학적 규칙을 따라야 한다.
- Are learned from examples (Realistic): 실제 분자 그래프를 모방해야 한다.

강화학습(Reinforcement Learning): ML agent는 Environment를 관찰(파악)하고, action을 취해 Environment와 상호작용을 하고, Reward를 받는다.
강화학습을 이용해 위의 언급된 규칙을 만족하게 한다.
GCPN
Graph Convolutional Policy Network = Graph representation(graph convolution) + Reinforcement Learning(policy)
key component
- Graph Neural Network가 그래프 구조적 정보를 포착한다.
- Reinforcement learning으로 desired objectives를 따르게 생성한다.
- Supervised training으로 주어진 데이터셋을 모방한다.
GCPN vs GraphRNN
공통점
- 순차적으로(sequentially) 그래프를 생성한다.
- 주어진 그래프 데이터셋을 모방한다.
차이점
-
GCPN은 generation action을 예측하기 위해 GNN을 사용한다.
- 장점: GNN이 RNN 보다 expressive 하다.
- 단점: GNN이 RNN 보다 연산(compute)하는데 오랜 시간이 걸린다.
-
GCPN은 RL을 사용해 goal-directed graph generation을 한다.
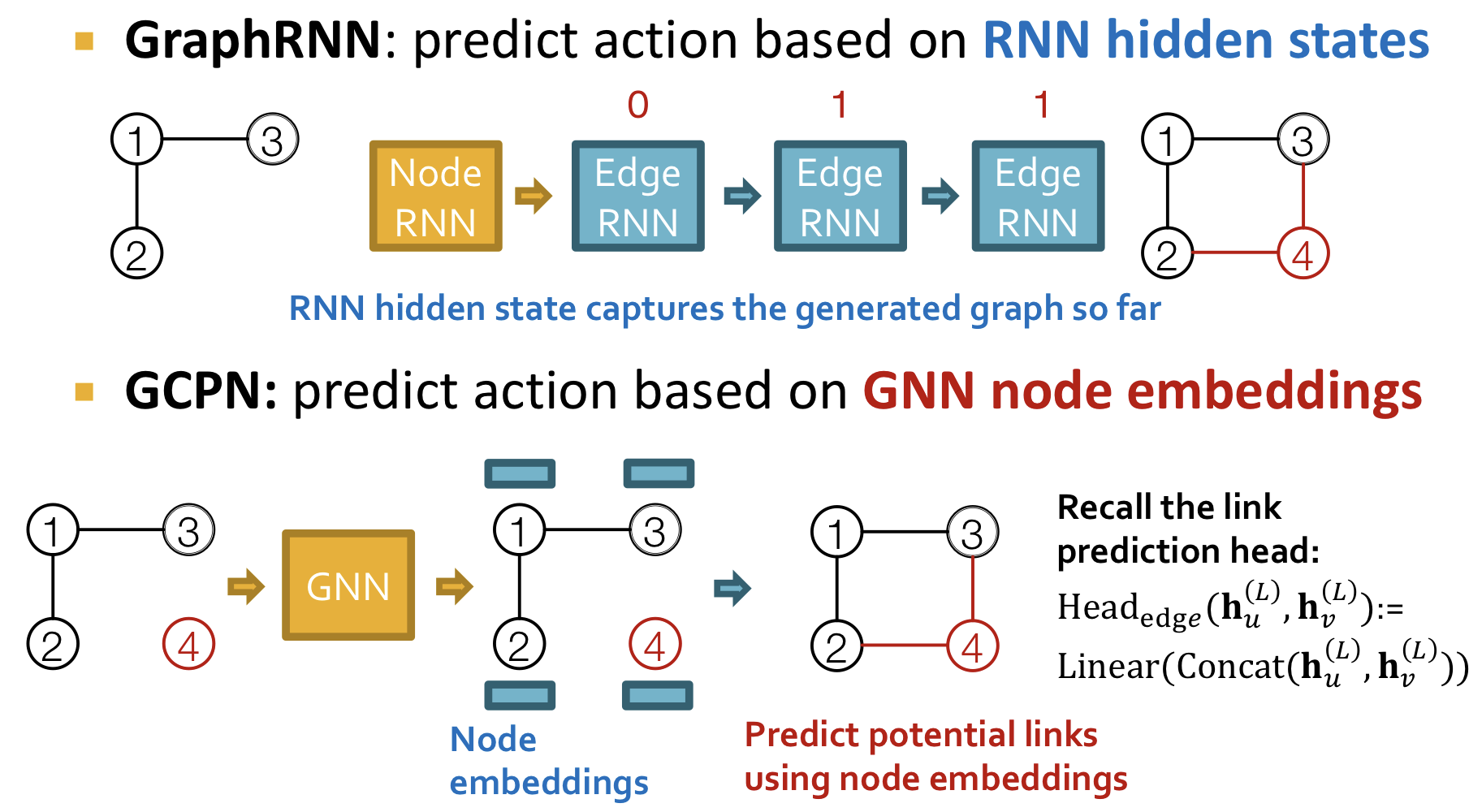
두 모델 모두 순차적으로(sequentially) node를 추가하면서 그래프를 생성하는데, edge를 연결하는 방법에 있어 차이가 존재한다. GraphRNN은 hidden states를 이용해 action(edge)을 예측한다. 반면에 GCPN의 경우 각각의 node embedding을 GNN을 통해 구한 후 prediction head를 통해 action(edge)을 예측한다.
Overview of GCPN
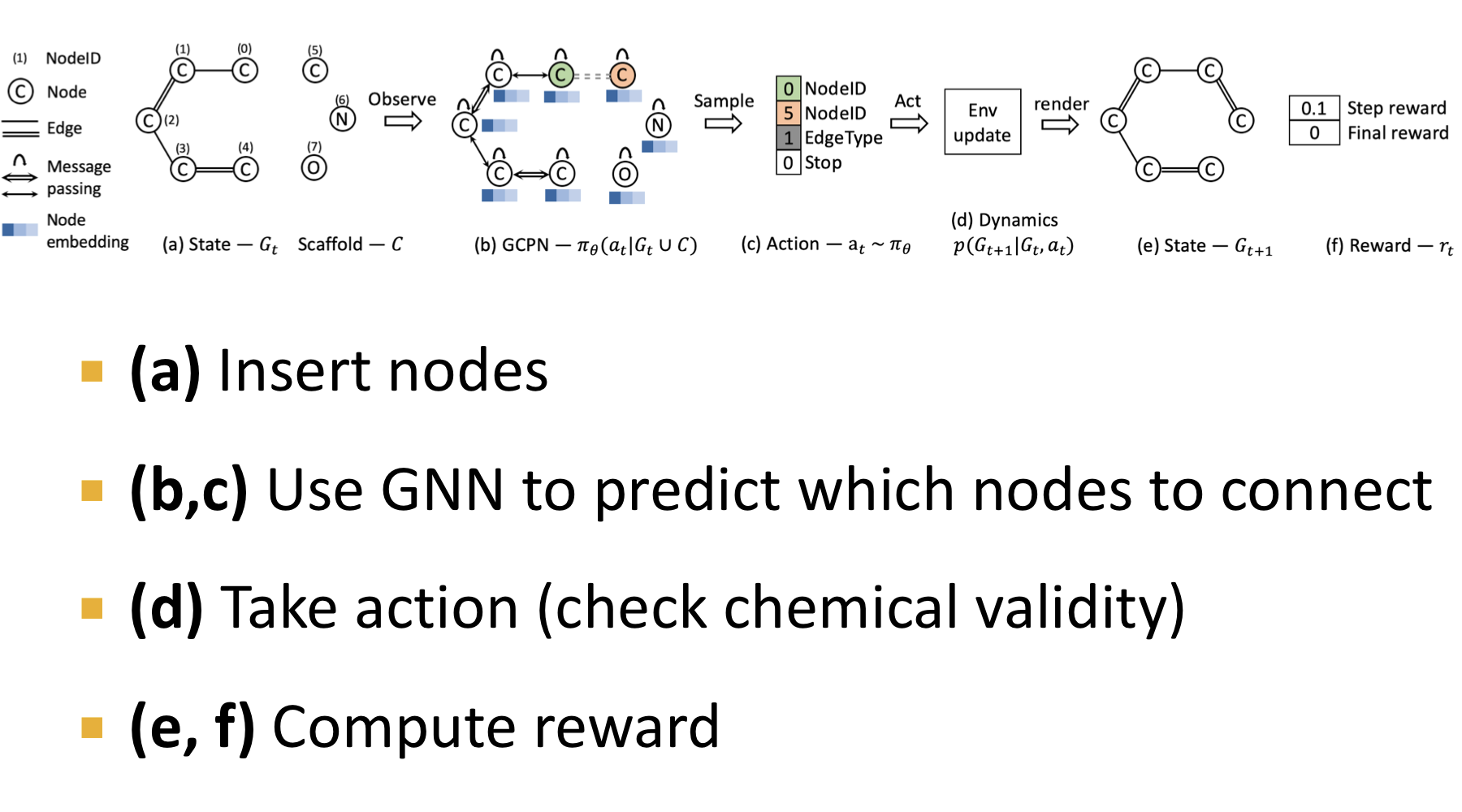
Train
강화학습을 진행하기 위해서는 reward를 정의해야 한다. GCPN에 두 종류의 reward의 합으로 이뤄진다.
- step reward: 각 단계마다 타당한 action을 했을 때 얻는 보상. 타당한 action은 타당하게 edge를 연결시킨 것
- final reward: 최종 단계에서 desired properties를 갖을 때 얻는 보상.
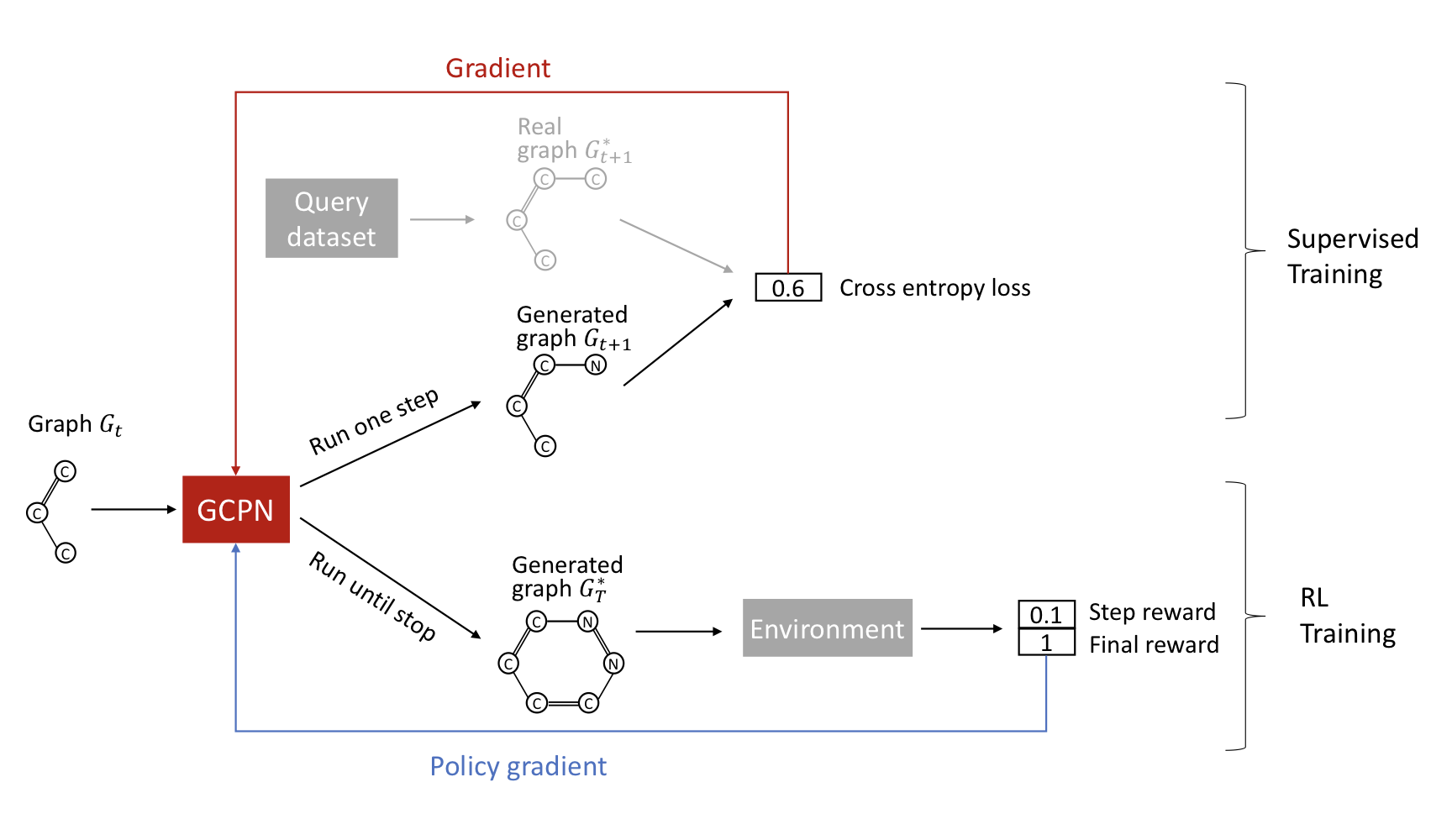
Training은 Supervised와 RL 두 부분으로 나뉜다.
- Supervised: Gradient를 사용해서 모델이 그래프 샘플들을 모방하게 학습
- RL: Policy gradient algorithm을 사용해서 보상이 최적화 되게 학습
Qaulitative Results
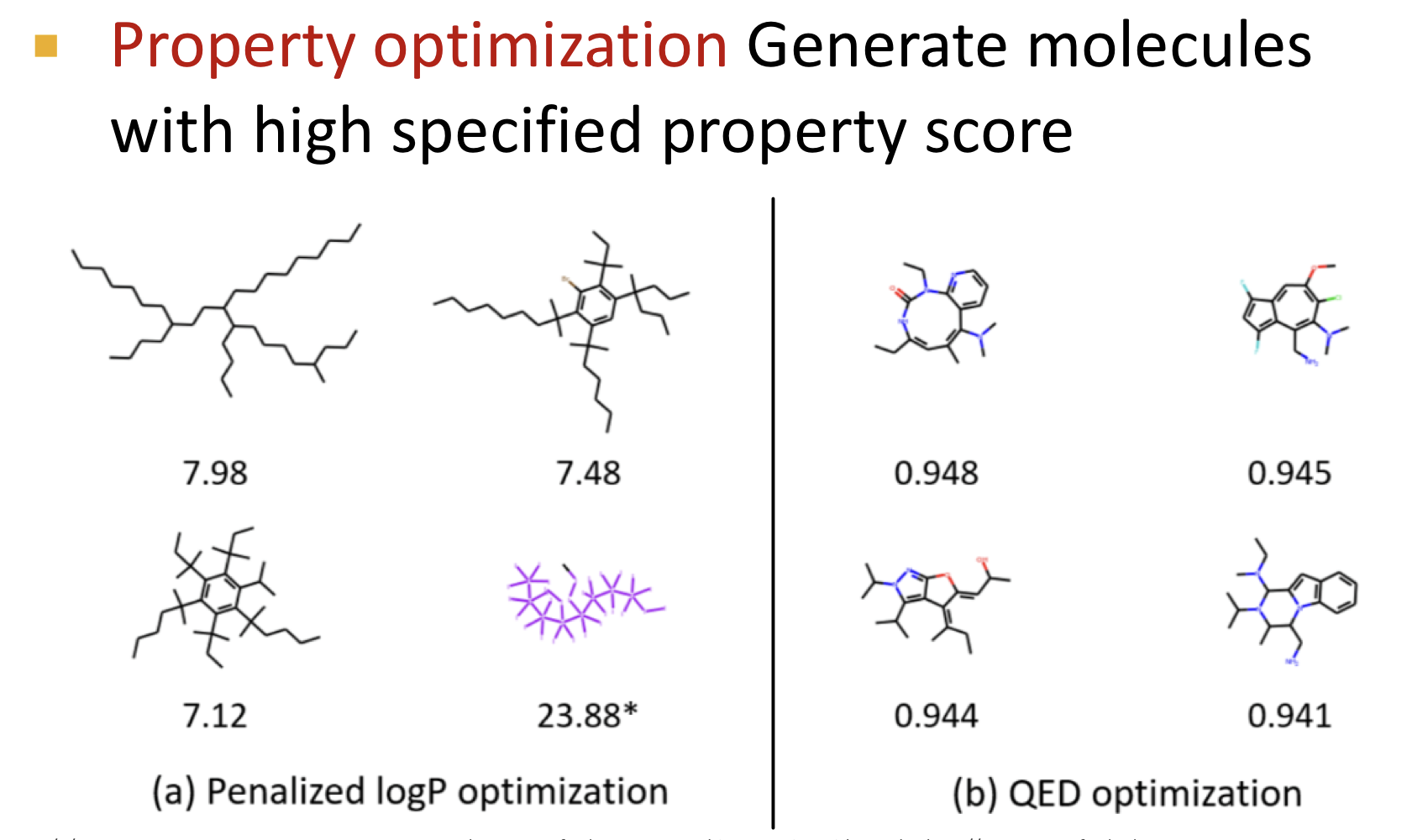
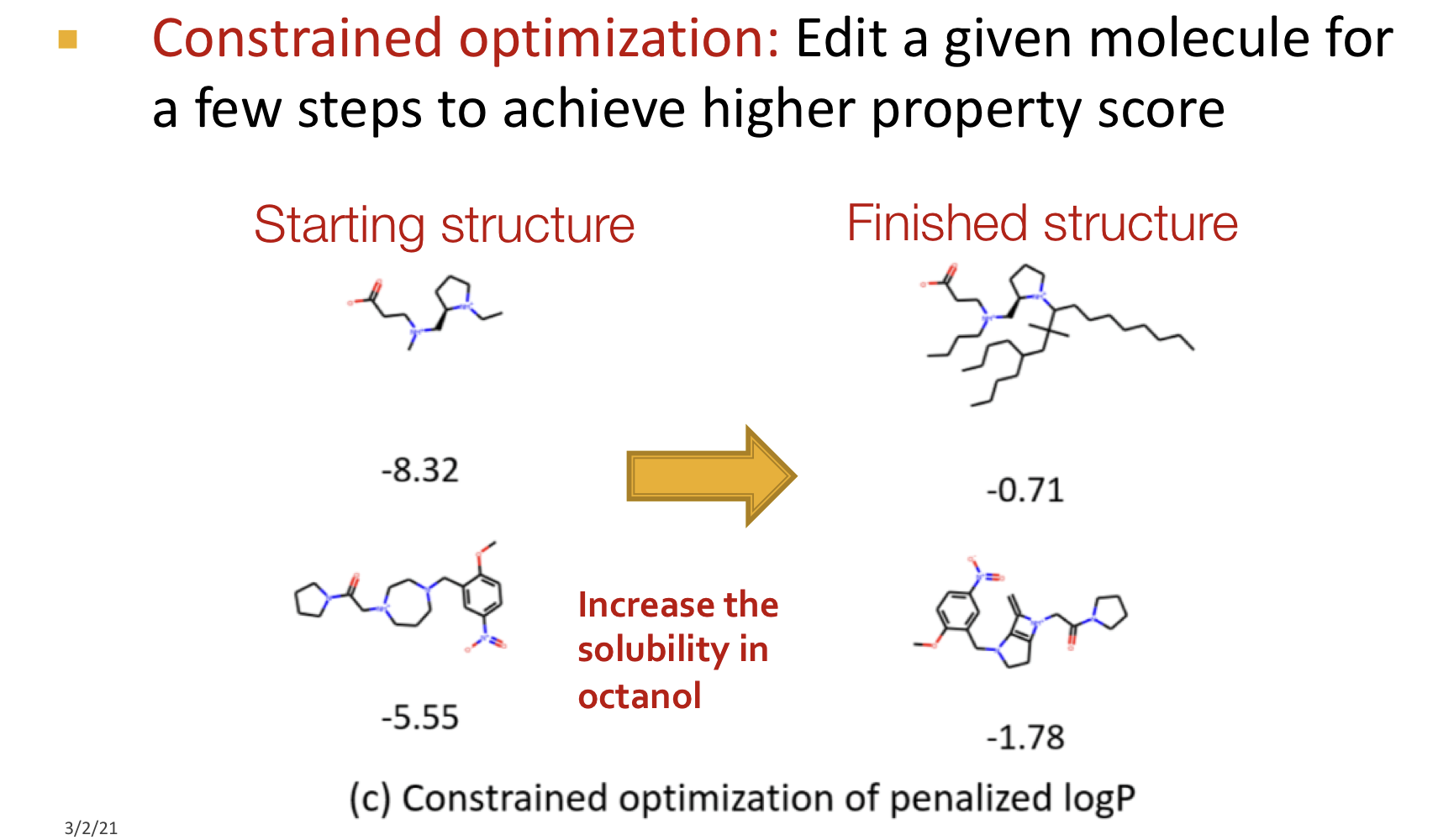
References
- CS224W: Machine Learning with Graphs (Winter 2021) 15강
- GraphRNN: Generating Realistic Graphs with Deep Auto-regressive Models 논문
- Wikipedia
- Wasserstein distance 관련 자료: https://www.youtube.com/watch?v=CDiol4LG2Ao
