[1주차] 디지털신호처리(DSP) 기초

Tobigs Sound Seminar·2021년 10월 9일
DSP
0

DSP

목록 보기
1/1

0. Audio Task

스마트 스피커 등의 voice agent의 등장으로 인해 음성 인터페이스의 중요도가 점점 커지고 있다. 먼저 1) 화자를 인식하여 voice agent를 wake하고, 2) 음성을 입력으로 받아 디바이스를 제어하고, 명령을 실행한 결과 또한 3) 음성 합성을 통해 출력된다. 이 과정과 관렫된 주요task로는 크게 세가지가 있다. Sound 분야에서는 Speech Classification과 Auto-tagging이 있고, Speech 분야에서는 음성인식(STT), 음성합성(TTS), 음성변환(STS) 등이 있다. 각각의 task에 대해 간단히 짚고 넘어가고자 한다.

0-1. Sound Classification & Auto-tagging

이미지 출처: http://dcase.community/challenge2020/task-acoustic-scene-classification

The goal of acoustic scene classification is to classify a test recording into one of the provided predefined classes that characterizes the environment in which it was recorded.

dcase라는 챌린지의 task 중 하나로 Acoustic Scene Classification이 있다. 다양한 device로부터 소리가 입력으로 주어질 때, 어떤 장소인지를 예측하는 문제이다. 위 과제를 수행하고 나면, 사용자가 위치하고 있는 장소 및 맥락을 이용하여 알맞은 서비스를 제공하는 데 활용될 수 있다.

0-2. STT (Speech-To-Text)

이미지 출처: https://paperswithcode.com/task/speech-recognition

STT는 음성을 텍스트로 변환하는 과업을 의미하며 ASR (Automatic Speech Recognition)이라 부르기도 한다. 특정 키워드를 찾거나 화자를 인식할 때도 사용되며, STT의 output을 NLP task의 input으로 연결시키기도 한다.

0-3. TTS (Text-To-Speech)

이미지 출처: https://myvoice.twip.kr/

텍스트를 입력으로 받아 사람의 음성처럼 합성해주는 task를 의미한다. 주로 text -> spectrogram 등의 intermediate representation -> speech 형태로 합성이 이뤄진다. text-> spectrogram 부분을 acoustic model, spectrogram -> speech 부분을 vocoder라 칭한다.

1. Digital Signal

1-1. Sound

소리의 물리량

소리는 일반적으로 진동으로 인한 공기의 압축으로 생성된다. 그압축이 얼마나 되었느냐에 따라서 표현되는 것이 바로 Wave(파동)이다. 파동은 진동하며 공간/매질을 전파해 나가는 현상이다. 질량의 이동은 없지만 에너지/운동량의 운반은 존재한다. 파동에서 얻을 수 있는 물리량은 크게 아래 세가지가 있다.

  1. Amplitude: 진폭
  2. Frequency: 주파수
  3. Phase: 위상

이미지 출처: https://blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=thddudghk0&logNo=221220483145

심리 음향

소리의 물리적 특성이 동일하더라도 소리는 종종 청자에 따라 다르게 인식되곤 한다. 공간에서 발생하는 소리라는 물리적 현상을 인간은 기계적으로 받아들이지 않고 주관적이고 감각적으로 인식하는 것을 연구하는 분야가 심리 음향이다.

이미지 출처: https://blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=tonmeistersu&logNo=70047115506

Sinusoid

정현파(Sinusoid)는 주기신호를 총칭하는 말이다. 정현파는 일반적으로 아래와 같은 방식으로 표현한다. 여기서 AA: 진폭, ω0\omega_0: 주파(=2πf)(=2\pi f), Φ\Phi: 위상을 의미한다.

오일러 공식: ejθ=cos⁡θ+jsin⁡θe^{j\theta}=\cos \theta + j \sin \theta

  1. 삼각함수에 의한 표현: x(t)=Acos⁡(ω0t+Φ)x(t) = A \cos (\omega_{0} t+\Phi)
  2. 복소지수에 의한 표현: x(t)=Re{Aej(ω0t+Φ)}=Aej(ω0t+Φ)+Ae−j(ω0t+Φ)2x(t) = Re\{Ae^{j(\omega_0 t+\Phi)}\}={Ae^{j(\omega_0 t+\Phi)}+Ae^{-j(\omega_0 t+\Phi)}\over 2}

Code: Sinusoid

def sinusoid(t, f, phi = 0):
    return np.cos(2 * np.pi * f * t + phi)
    
def complex_sinusoid(t, f, phi=0):
    cSin = np.exp(1j*(2 * np.pi * f * t + phi))+np.exp(-1j*(2 * np.pi * f * t + phi))
    return cSin/2

def uniform_samples(sr, dur):
    return np.arange(sr * dur) / sr

def sinusoid_samples(sr, f = 8000, dur = 1, isComplex = False):
    ts = uniform_samples(sr, dur)
    if isComplex:
        sin = complex_sinusoid(ts, f)
    else:
        sin = sinusoid(ts, f)
    return ts, sin

import librosa.display

sr = 48000
fig, ax = plt.subplots(2, sharex = 'all')
ts, sin = sinusoid_samples(sr, isComplex = False)
ax[0].plot(ts[:100], sin[:100])
ax[0].set_title("Real Sinusoids")

cts, csin = sinusoid_samples(sr, isComplex = True)
ax[1].plot(cts[:100], csin[:100])
ax[1].set_title("Complex Sinusoids")

ax[1].set_xlabel("time (sec)")
fig.tight_layout()
plt.show()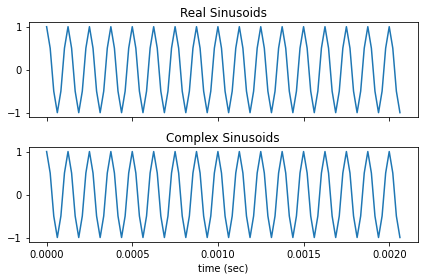

1-2. Sampling & Quantization

소리는 연속적인 데이터이다. 소리 데이터를 컴퓨터에 저장하기 위해서는 Sampling과 Quantization을 통해 discrete하게 표현해야 한다. 먼저, 실수형태인 시간을 저장하기 위해 sampling을 진행한다.

Sampling이란?

시간을 이산적인 구간으로 나누는 것이다. 즉, 샘플링 간격에 따라 amplitude를 측정하는 것이다. 1초의 연속적인 신호를 몇개의 숫자들의 sequence로 표현할 것인가를 sampling rate fsf_s이다.

xs[n]=xc(nTs)=xc(nfs)x_s[n] = x_c(nT_s)=x_c\begin{pmatrix}{n\over f_s}\end{pmatrix}

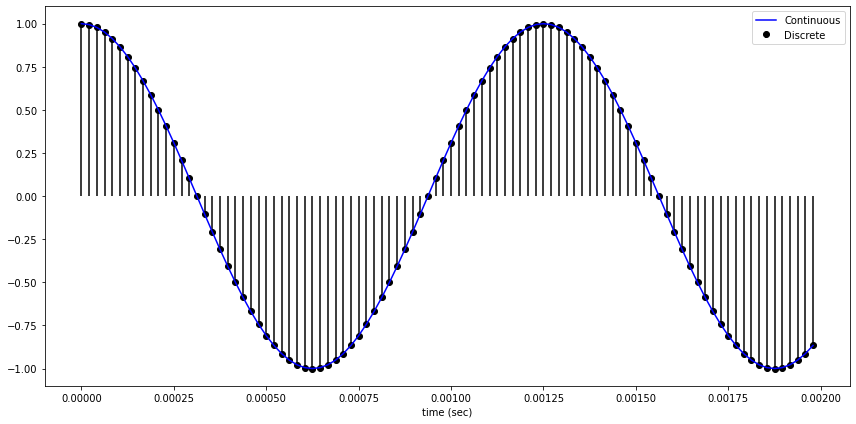
sampling rate가 클수록 즉, 자주 sampling할 수록 원본 데이터와 비슷할 것이다. 그러나 그만큼 저장해야 하는 데이터의 양이 늘어나게 된다. sampling rate가 작게 되면 아래와 같이 aliasing이 일어나 원본 데이터로 복원하는 데 어려움을 겪을 수 있다. 붉은 선이 원래 신호인데, sampling rate가 낮은 경우 원래 신호보다 주파수가 낮은 검은색 점선 형태로 복원될 수 있다.

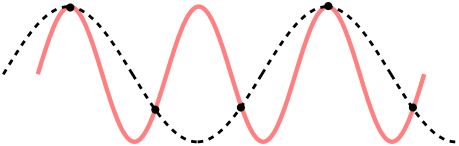이미지 출처: https://ko.m.wikipedia.org/wiki/%EC%9C%84%EC%8B%A0%ED%98%B8

Nyquist 이론에 의해 sampling rate가 원래 신호에 존재하는 주파수의 최댓값의 2배 보다 크면 원래 신호를 손실없이 복원할 수 있다.

즉, fs>fm,fmf_s > f_m, f_m은 최대 주파수를 의미한다. 일반적으로 Audio CD의 경우 44.1kHz, Speech는 8kHz의 sampling rate를 사용한다.
참고: Alias-Free GAN

Code: Sampling

import IPython.display as ipd

wav, sr = librosa.load(librosa.ex('brahms'), duration = 5)
for new_sr in [sr, 16000, 8000, 4000]:
    new_wav = librosa.resample(wav, sr, new_sr)
    print("Sampling rate:", new_sr)
    ipd.display(ipd.Audio(new_wav, rate=new_sr))

Quantization이란?

Amplitude를 이산적인 구간으로 나누고, signal 데이터의 Amplitude를 반올림하여 저장한다. 보통 bit로 나타낸다.

  • B bit의 Quantization : −2B−1-2^{B-1} ~ 2B−1−12^{B-1}-1
  • Audio CD의 Quantization (16 bits) : −215-2^{15} ~ 215−12^{15}-1

위 값들은 보통 -1.0 ~ 1.0 영역으로 scaling하기도 한다.

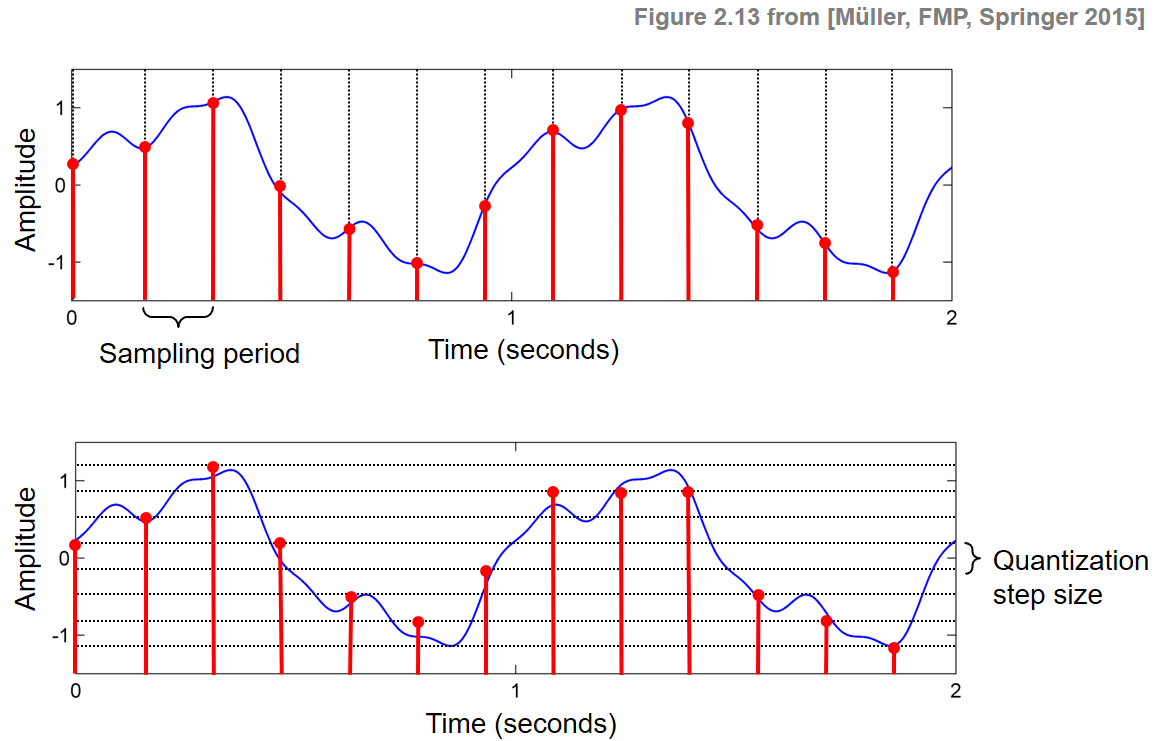이미지 출처: https://www.audiolabs-erlangen.de/resources/MIR/FMP/C2/C2S2_DigitalSignalQuantization.html

Code: Quantization

wav, sr = librosa.load(librosa.ex('brahms'), duration = 5)
normed_wav = wav / max(np.abs(wav))
print("Scaled to [-1., 1.]")
ipd.display(ipd.Audio(normed_wav, rate=sr))

Bit = 4
max_value = 2 ** (Bit-1)
quantized_8_wav = normed_wav * max_value
quantized_8_wav = np.round(quantized_8_wav).astype(int)
quantized_8_wav = np.clip(quantized_8_wav, -max_value, max_value-1)
print(Bit, "bit Quantization")
ipd.display(ipd.Audio(quantized_8_wav, rate=sr))

2. Fourier Transforms

푸리에 변환(Fourier transform)을 직관적으로 설명하면 푸리에 변환은 임의의 입력 신호를 다양한 주파수를 갖는 주기함수(복수 지수함수)들의 합으로 분해하여 표현하는 것이다. 그리고 각 주기함수들의 진폭을 구하는 과정을 퓨리에 변환이라고 한다.

2-1. Fourier Series

1807년 푸리에는 임의의 함수를 삼각함수의 (무한) 선형조합으로 표현할 수 있다고 주장하였다. (참고)

이미지 출처: https://link.springer.com/chapter/10.1007/978-3-030-60515-5_22

힐버트 공간 F=L2([0,2π])\mathcal{F}=L^2([0, 2\pi]) 상에서 지수함수계 E={12πejnt:n=0,±1,±2,⋯}E=\begin{Bmatrix}{1\over\sqrt{2\pi}}e^{jnt} : n=0, \pm1, \pm2, \cdots \end{Bmatrix}는 완비정규직교 기저집합이므로 [0,2π][0, 2\pi]에서 정의되는 주기함수들은 다음과 같이 푸리에 급수로 표현된다.

x(t)=∑n=−∞∞an12πejntan=⟨f,pn⟩=∫02πx(t)12πe−jntdtx(t)=\sum_{n=-\infty}^\infty a_n {1\over \sqrt{2\pi}}e^{jnt} \\ a_n=\left\langle f, p_n\right\rangle=\int_0^{2\pi}x(t){1\over \sqrt{2\pi}}e^{-jnt}dt

먼저 첫번째 식을 보면 nn는 −∞-\infty ~ ∞\infty의 범위를 가지고 움직인다. 즉, 어떠한 신호가 서로 다른 주기함수들의 합으로 표현되는데, 그 주기함수는 무한개가 있어야 함을 의미한다.
한가지 더 주목할 점은 지수함수계의 함수들이 모두 직교한다는 점이다. 즉, x(t)x(t)는 기저를 E로 두면, (a−∞,⋯ ,a∞)\left( a_{-\infty}, \cdots, a_\infty\right)라는 좌표로 표현할 수 있게 된다.

2-2. DFT (Discrete Fourier Transform)

Fourier Transform

위 결과를 주기가 무한대인 일반적인 함수로 일반화하면, Fourier Transform 식을 얻을 수 있다.

Inverse Fourier Transform: x(t)=12π∫−∞∞X(jω)ejωtdωFourier Transform: X(jω)=∫−∞∞x(t)e−jωtdt\text{Inverse Fourier Transform: }x(t)={1\over 2\pi}\int_{-\infty}^\infty X(j\omega)e^{j\omega t} d\omega\\ \text{Fourier Transform: }X(j\omega)=\int_{-\infty}^\infty x(t)e^{-j\omega t} dt

즉, time domain에서 연속적이고 무한한 길이의 신호를 frequency domain에서 연속적이고 무한한 주파수로 나타낼 수 있다.

Discrete Fourier Transform

우리가 sampling한 신호는 바로 시간의 간격과 소리의 amplitude가 모두 discrete한 데이터이다. 따라서 위의 푸리에 변환 식을 Discrete한 영역으로 바꾸어야 한다. 연속적인 신호에서 N개 샘플링한 이산적인 신호에서는 다음과 같이 푸리에 급수로 표현된다.

Inverse Discrete Fourier Transform: x[t]=1N∑k=0N−1X[k]ejωknDiscrete Fourier Transform: X[k]=∑n=0N−1x[n]e−jωkn\text{Inverse Discrete Fourier Transform: }x[t]={1\over N}\sum_{k=0}^{N-1} X[k]e^{j\omega_kn} \\ \text{Discrete Fourier Transform: }X[k]=\sum_{n=0}^{N-1}x[n]e^{-j\omega_k n}

우리가 가진 신호 x[t]x[t]에서, 이산 시계열 데이터가 주기 NN으로 반복한다고 할때, DFT는 주파수와 진폭이 서로 다른 NN개의 사인 함수의 합으로 표현이 가능하다.

위 식을 보면 k의 range가 0부터 N−1N-1로 변화했음을 알 수 있다. 이때 Spectrum X[k]X[k]를 원래의 시계열 데이터에 대한 퓨리에 변환값이라 한다.

이미지 출처: https://dsp.stackexchange.com/questions/646/what-is-the-most-lucid-intuitive-explanation-for-the-various-fts-cft-dft-dt

Zero Padding

이미지 출처: https://flylib.com/books/en/2.729.1/dft_resolution_zero_padding_and_frequency_domain_sampling.html

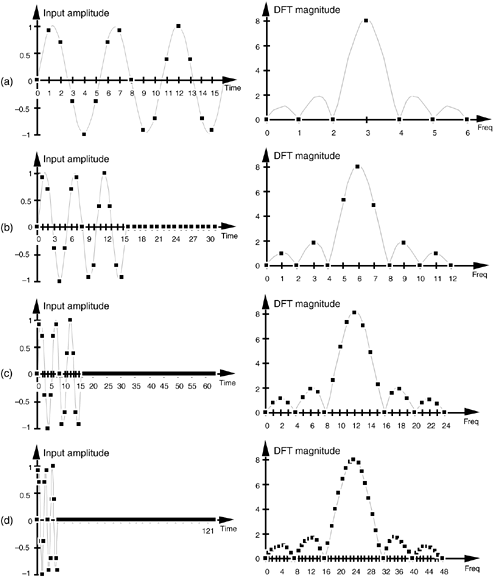
첫번째 행의 입력 신호의 길이가 짧기 때문에 DFT로 나온 스펙트럼 또한 적은 개수의 주파수만을 표현할 수 있다. 즉, 신호의 길이가 짧아서 DFT 된 신호가 정확히 표현되지 않은 경우이다. 좀 더 정확한 주파수 영역의 신호를 얻기 위해서는, 위의 예시와 같은 문제점을 해결해야한다. 이 때 사용하는 방법이 바로 zero-padding 이다. zero padding은 x(n)의 뒤에 0을 여러개 덧붙여서 강제로 x(n)의 길이를 늘려줌으로써 DFT된 X(m)을 더 촘촘하게 나타내는 방법이다.

신호의 뒤에 0을 덧붙여 DFT 를 수행한다면, 샘플 수가 늘어난 X(m)을 얻을 수 있다. 이러한 방식으로 고밀도의 스펙트럼을 얻을 수 있다 신호의 샘플 수는 늘어나게 되어 X(m)이 더욱 촘촘한 간격의 한주기 신호로 생성되었고, 단순히 0을 덧붙였으므로 신호의 특성이나 분해능에는 영향을 미치지 않는다. 따라서, zero padding은 고밀도의 스펙트럼을 얻게 해주지만 고분해능의 스펙트럼을 얻을 수 있는 것은 아니다.

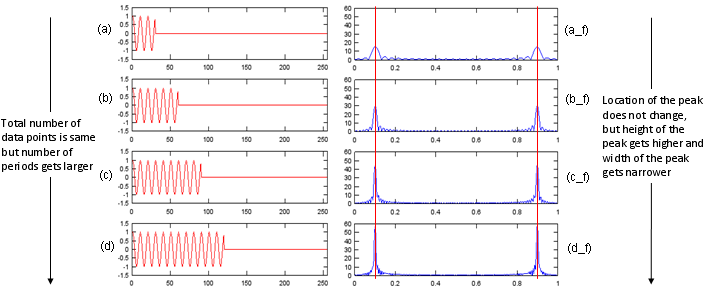
이미지 출처: https://www.sharetechnote.com/html/Eng_FFT.html

위 그림과 같이 실제로 신호의 길이가 길어진 경우와 단순히 zero padding을 붙여서 신호의 길이를 길게 만든 경우의 스펙트럼은 다르게 나타난다. 신호의 길이가 길어진 경우 main lobe가 점점 좁아지는 것을 확인할 수 있다.

신호의 길이가 길어지면 원래 신호의 주파수가 어떻게 분포하는지를 정확하게 파악할 수 있다. 반면에 zero padding을 붙인 경우는 위에서 볼 수 있듯이 고밀도로 간격은 좁아졌지만 main lobe의 폭은 변화가 없기 때문에 고분해능이라 보기는 힘들다.

Code: DFT

def DFT(x):
    N = len(x)
    X = np.array([])
    nv = np.arange(N)
    for k in range(N):
        s = np.exp(1j*2*np.pi*k/N*nv)
        X = np.append(X, sum(x*np.conjugate(s)))
    return X

def plot_magnitude(DFT, ax, N):
    magnitude = np.abs(DFT)
    freq_axis = 2 * np.pi * np.arange(magnitude.shape[-1]) / N
    ax.stem(freq_axis, magnitude, 'k', markerfmt = 'ko', basefmt = " ", use_line_collection = True)
    ax.set(title="Magnitude of DFT", xlim = (0, np.pi), xticks=[0, np.pi / 2, np.pi], xticklabels=[r'$0$', r'$\pi/2$', r'$\pi$'], xlabel = 'Frequency (rad)', ylabel='Manigude')

def plot_phase(DFT, ax, N):
    phase = np.angle(DFT)
    freq_axis = 2 * np.pi * np.arange(magnitude.shape[-1]) / N
    ax.stem(freq_axis, phase, 'k', markerfmt = 'ko', basefmt = " ", use_line_collection = True)
    ax.set(title="Phase of DFT", xlim = (0, np.pi), xticks=[0, np.pi / 2, np.pi], xticklabels=[r'$0$', r'$\pi/2$', r'$\pi$'], xlabel = 'Frequency (rad)', 
           ylabel='Phase (rad)', ylim=(-np.pi, np.pi),  yticks=[-np.pi, 0, np.pi], yticklabels=[r'$-\pi$', r'$0$', r'$\pi$'])

num_samples = 47
sinusoid = np.cos(np.pi * 2 / 5.5 * np.arange(num_samples))
X = DFT(sinusoid)
fig, axes = plt.subplots(ncols=3)
axes[0].stem(np.arange(num_samples), sinusoid, 'k', markerfmt = 'ko', basefmt = " ", use_line_collection = True,)
axes[0].set(title="Discrete signal", xlabel="Discrete index", ylabel="Amplitude")
plot_magnitude(X, axes[1], sinusoid.shape[-1])
plot_phase(X, axes[2], sinusoid.shape[-1])
fig.set_size_inches(18, 6)
fig.tight_layout()
plt.show()

DFT의 실제 구현은 FFT를 이용하기 때문에 O(nlogn)O(nlogn)의 시간복잡도를 가진다. (참고)

2-3. STFT (Short Time Fourier Transform)

spectrogram vs spectrum

wav, sr = librosa.load(librosa.ex("brahms"), duration = 3)
ipd.display(ipd.Audio(wav, rate=sr))
S = librosa.core.stft(wav, n_fft=1024, hop_length=512, win_length=1024)
log_S = librosa.power_to_db(np.abs(S)**2, ref=np.max)

fig, axes = plt.subplots(ncols=2)
plot_magnitude(np.fft.rfft(wav), axes[0], wav.shape[-1])

librosa.display.specshow(log_S, sr=sr, x_axis='time', y_axis='hz', ax = axes[1])
axes[1].set_title("STFT")
fig.set_size_inches(12, 4)
fig.tight_layout()
plt.show()

왼쪽 그림이 spectrum이고, 오른쪽 그림이 spectrogram이다. spectrum과 spectrogram의 가장 큰 차이는 시간 축의 유무이다.

spectrum은 시간 축이 없기 때문에 특정 시간대의 snapshot을 찍어 소리의 에너지를 분석한 것이다. 반면에 spectrogram은 시간에 따른 소리의 변화를 시각화한 것이다.

대부분의 신호는 시간에 따라 주파수가 변하게 된다. 그러나 FFT는 어느 시간대에 주파수가 변하는지 알 수 없다. 즉 FFT를 하면 Time domina에 대한 정보가 사라진다. 이러한 한계를 극복하기 위해서, STFT는 시간을 프레임별로 나눠서 FFT를 수행한다.

STFT

X(l,k)=∑n=0N−1w(n)x(n+lH)exp⁡−2πknNX(l,k) = \sum_{n=0}^{N-1} w(n) x(n+lH)\exp^{\frac{-2\pi k n}{N}}

STFT는 주파수의 특성이 시간에 따라 달라지는 사운드를 분석하는 방법이다. speech signal의 특성이 상대적으로 느리게 변한다고 가정하고, 짧은 시간간격 안에서는 stationary하다고 가정한다. 짧은 시간간격으로 나누는 framing과정을 거쳐서 short-time에 대한 processing을 하게된다. 시계열 데이터를 일정한 시간 구간 (window size)로 나누고, 각 구간에 대해서 스펙트럼을 구하는 데이터이다. 따라서 STFT를 수행하면, (time, frequncy, magnitude) 꼴로 spectrogram이 나온다. 시각화할 때는 일반적으로 시간을 x축으로, 주파수를 y축으로, 크기를 색깔로 표현한다.

Parameter of STFT

  • NN : FFT size

    • Window를 얼마나 많은 주파수 밴드로 나누는가

  • w(n)w(n) : Window function

    • 일반적으로 Hann window가 쓰인다.

  • nn : Window size

    • Window 함수에 들어가는 Sample의 양이다.
    • 작을수록 Low-frequency resolution을 가지게 되고, high-time resolution을 가진다.
    • 길수록 High-frequency, low time resolution을 가진다.

  • HH : Hop size

    • 윈도우가 겹치는 사이즈이다. 일반적으로는 1/2 혹은 1/4정도를 겹치게 한다.

3. Convolution Theorem

Convolution

(x∗y)[n]:=∑m=−∞∞x[m]y[n−m](x∗y)(t):=∫−∞∞x(τ)y(t−τ)dτ(x*y)[n]:=\sum_{m=-\infty}^\infty x[m]y[n-m]\\ (x*y)(t):=\int_{-\infty}^\infty x(\tau)y(t-\tau)d\tau

Circular Convolution

(x⊛y)[n]:=∑m=0N−1x[m]y[(n−m)N](x⊛y)(t):=∫τ=0Tx(τ)y((t−τ)T)dτ(x\circledast y)[n]:=\sum_{m=0}^{N-1}x[m]y[(n-m)_N]\\ (x\circledast y)(t):=\int_{\tau=0}^T x(\tau)y\left((t-\tau)_T\right)d\tau

3-1. Convolution Theorem

한 도메인에서의 convolution은 다른 도메인에서의 element-wise multiplication이다. 역도 성립한다.

증명은 여기를 참고하면 된다. convolution은 주파수 도메인에서의 연산과 시간 도메인에서의 연산을 자유자재로 변환할 수 있기 때문에 계산 효율을 높일 때도 많이 쓰인다. 이 외에도 LTI 시스템을 분석할 때도 사용된다. (참고)

3-2. Window

STFT의 parameter 중에는 window라는 것이 있다. STFT는 signal을 frame별로 잘라서 FFT를 수행하는데, frame을 어떻게 자를 것인지 결정하는 것이 window이다. 일반적으로는 frame간의 불연속성을 없애주기 위해 양 끝단을 0으로 만드는 window함수를 사용한다. 아래 그림은 hann window를 사용하여 DFT를 수행한 결과이다. 

num_samples = 47
sinusoid = np.cos(np.pi * 2 / 5.5 * np.arange(num_samples))
sinusoid_windowed = sinusoid * np.hanning(len(sinusoid))
fig, axes = plt.subplots(1, 2)

for idx, (win, wav) in enumerate([("rectangular", sinusoid), ("hann", sinusoid_windowed)]):
    color = ["k", "g"][idx]
    X = DFT(wav)
    axes[0].stem(np.arange(num_samples), wav, color, markerfmt = color+'o', basefmt = " ", use_line_collection = True, label = win)
    axes[0].set(title="Discrete signal", xlabel="Discrete index", ylabel="Amplitude")
    plot_magnitude(X, axes[1], wav.shape[-1], c= color, label = win)
    
fig.set_size_inches(10, 4)
fig.tight_layout()
plt.legend()
plt.show()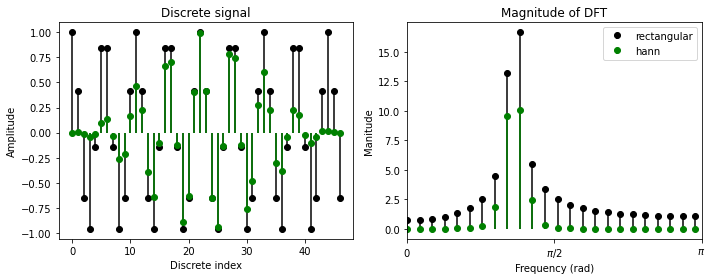


hann window를 취하게 되면 amplitude의 크기는 작아졌지만 side lobe의 크기가 굉장히 작아진 것을 확인할 수 있다. 즉, spectral leakage를 막을 수 있기 때문에 신호에 window를 취해 FFT를 수행한다.

rectangular window(No window)를 취했을 때, spectral leakge가 나오는 현상을 Convolution theorem을 이용하여 설명할 수 있다. 위 그림은 단일 sinusoid signal에 FFT를 수행한 것이다. 그럼에도 불구하고 Frequency가 하나로 나오지 않는다. 윈도우를 아무것도 적용하지 않은 경우 time domain에서 signal과 rectangular window의 element-wise multiplication이다. 이를 주파수 도메인에서 보면 convolution연산으로 바뀌게 된다. 아래 그림은 다양한 window들에 FFT를 적용하여 주파수 도메인으로 바꾼 것이다. 즉, 원래 신호의 스펙트럼에 rectangular window의 스펙트럼이 convolution이 되기 때문에 FFT를 수행한 결과에 spectral leakage가 발생하게 된다. hann window가 rectangular window보다 leakage가 적게 발생하는 이유도 아래 그림을 통해 알 수 있다.

이미지 출처: https://www.researchgate.net/publication/273339582_A_Comparative_Study_of_State-of-the-Art_HighPerformance_Spectral_Test_Methods/link/5665a55f08ae15e74634a522/download

4. Ceptrum Analysis

4-1. Speech Model

(출처: 카카오엔터프라이즈 TECH LOG)

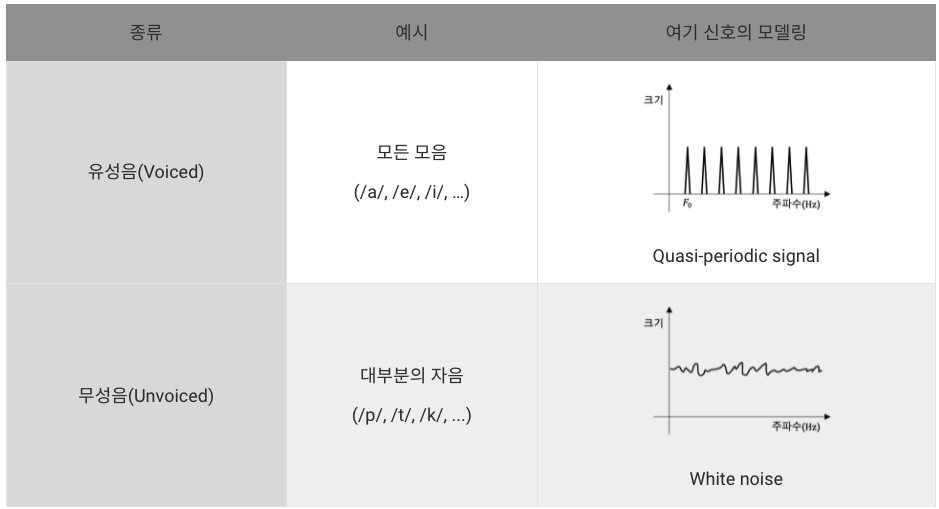
발음을 결정하는 소리의 최소 단위인 음소(phoneme)는 크게 2가지로 구분할 수 있는데, 발성할 때 성대(vocal cord)의 진동을 동반하는 유성음(voiced)과 진동 없이 성대를 통과하는 무성음(unvoiced)이 있다. (출처: 다음백과)
사람의 발성 구조를 공학적으로 해석할 때, 성대를 막 통과한 소리를 여기 신호(excitation signal)라고 부른다. 이때 유성음 여기 신호의 파형은 준주기성(quasi-periodic)을 띄게 되며, 성대의 진동 속도에 따라 고유의 기본 주파수(fundamental frequency)와 기본 주파수의 배수에 해당하는 여러 배음(harmonics)들로 전체 스펙트럼이 구성된다. 반면, 무성음 여기 신호의 파형은 성대가 진동하지 않아 다양한 주파수 성분이 고르게 포함된 백색소음(white noise)과 같은 스펙트럼을 갖는다.

이미지 출처: https://tech.kakaoenterprise.com/66

위 그림은 사람이 음성을 만들 때 사용하는 기관들의 동작과 이들을 각각 공학적으로 모델링한 특징 정보들의 관계를 나타낸다. 처음 폐에서 만드는 압축된 공기는 백색소음에 가까운 비주기성(aperiodicity) 신호로, 정규분포와 같이 쉽게 사용할 수 있는 확률분포로 모델링할 수 있다. 성대를 통과한 직후의 여기 신호는 유성음/무성음 여부에 따라 구분되며, 유성음의 경우 기본 주파수 등의 특징을 담고 있다. 이후 목, 코, 입, 혀 등의 성도(vocal tract)를 통과하며 발음이 결정되는데, 발음마다 성도의 구조가 달라져 증폭되는 주파수 대역과 감쇠되는 대역 역시 달라지게 된다. 이를 스펙트럼 포락선(spectral envelope)이라고 하며, 발음의 종류를 결정하는 주요한 특징으로 꼽힌다.

이미지 출처: https://hyunlee103.tistory.com/45

4-2. Ceptrum Analysis

이미지 출처: https://www.researchgate.net/publication/26335113_Automatic_Detection_of_Laryngeal_Pathologies_in_Records_of_Sustained_Vowels_by_Means_of_MelFrequency_Cepstral_Coefficient_Parameters_and_Differentiation_of_Patients_by_Sex

위에서 보았듯이 발음 혹은 음색 등을 결정하는 주요한 특징으로는 spectral envelope가 있다. 왼쪽 그림은 FFT를 거쳐서 얻은 스펙트럼이다.

spectral evelope를 얻기 위해서는 DFT -> log -> IDFT -> liftering -> DFT 형태로 연산한다.

"음성 신호의 스펙트럼 S(f) = 빠른 신호의 스펙트럼 X(f) * 느린신호의 스펙트럼 h(f)"꼴로 나타난다. 즉, S(f)=X(f)H(f)S(f) = X(f)H(f)이다. 여기에 로그를 취하면, log⁡∣S(f)∣=log⁡∣X(f)H(f)∣=log⁡∣X(f)∣+log⁡∣H(f)∣\log |S(f)| = \log |X(f)H(f)| = \log |X(f)| + \log|H(f)|가 된다. 즉, 빠른신호와 느린신호가 덧셈의 형태로 존재하게 되며, 이 신호를 다시 IDF를 취하면 시간축과 주파수축의 duality 성질 때문에 느린 신호는 time축의 낮은 영역(0과 가까운 부분)에 존재하며, 빠른 신호는 time축의 높은 영역에 존재한다.DFT를 수행하고 IDFT를 수행하였는데, 그 결과는 마치 주파수측의 모양을 주파수 분해한것과 같은 상태가 된다. 그래서 붙여진 이름이 spec을 거꾸로하여 cepstrum이다.

그럼 여기서 envelope을 얻기위해서 time축의 낮은 영역을 가져온다. 이것도 주파수 축에서 lowband를 가져오는 것과 비슷한 형태이기 때문에 주파수축에서 수행하던 filtering의 이름을 바꿔서 liftering이라 부른다. 이 리프터링 된 신호를 다시 DFT하면 왼쪽의 spectral envelope를 얻을 수 있다.

4-3. MFCC

Mel Scale

이미지 출처: https://tech.kakaoenterprise.com/66

일반적으로 사람은, 인접한 주파수를 크게 구별하지 못한다. 그 이유는 우리의 인지기관이 categorical한 구분을 하기 때문이다. 때문에 우리는 주파수들의 Bin의 그룹을 만들고 이들을 합하는 방식으로, 주파수 영역에서 얼마만큼의 에너지가 있는지를 찾아본다. 일반적으로는 인간이 낮은 주파수에 더 풍부한 정보를 사용하기 때문에, 주파수가 올라갈수록 필터의 폭이 높아지면서 고주파는 거의 고려를 안하게 된다. 이는 달팽이관의 가장 안쪽 청각 세포는 저주파 대역을 인지하며, 바깥쪽 청각 세포는 고주파 대역을 인지한다는 점을 모델링한 것이다. 실제로도 모든 주파수 대역을 같은 비중으로 인지하지 않고, 고주파에서 저주파로 내려갈수록 담당하는 주파수 대역이 점점 더 조밀해진다.

이미지 출처: https://en.wikipedia.org/wiki/Mel_scale

멜 스펙트럼은 주파수 단위를 아래 공식에 따라 멜 단위로 바꾼 것을 의미한다. 일반적으로는 mel-scaled bin을 FFT size보다 조금 더 작게 만든다.
m=2595log⁡10(1+f700)m = 2595 \log_{10}\left(1 + \frac{f}{700}\right)

보통은 Mel Filter Bank를 사용하여 구현한다.

filter_banks = np.dot(pow_frames, fbank.T)
filter_banks = np.where(filter_banks == 0, np.finfo(float).eps, filter_banks)  # Numerical Stability

이미지 출처: https://ratsgo.github.io/speechbook/docs/fe/mfcc

MFCC (Mel-frequency Cepstral Coefficients)

멜 스펙트럼 혹은 로그 멜 스펙트럼은 태생적으로 피처(feature) 내 변수 간 상관관계(correlation)가 존재한다. 위에서 본 그림을 통해 알 수 있듯이 주변 몇 개의 헤르츠 기준 주파수 영역대 에너지를 한데 모아 보기 때문아다. 변수 간의 종속성을 해결하기 위해 로그 멜 스펙트럼에 역푸리에 변환(Inverse Fourier Transform)을 수행해 변수 간 상관관계를 해소한 피처가 MFCC이다. MFCC는 다음의 과정을 거쳐서 만들어진다.

  1. waveform
  2. Magnitude Spectrogram (by STFT)
  3. Mel Spectrogram (by Mel Filterbank)
  4. Log-Mel Spectrgoram
  5. MFCC (by Discrete Cosine Transform)

DCT는 n개의 데이터를 n개의 코사인 함수의 합으로 표현하여 데이터의 양을 줄이는 방식이다. 로그 멜 스펙트럼에 DCT 변환을 실시하면 상관관계가 높았던 주파수 도메인 정보가 새로운 도메인으로 바뀌어 이전 대비 상대적으로 변수 간 상관관계가 해소되게 된다. 그러나 멜 스펙트럼 혹은 로그 멜 스펙트럼 대비 MFCCs는 구축 과정에서 버리는 정보가 지나치게 많습니다. 이 때문인지 최근 딥러닝 기반 모델들에서는 MFCC보다는 멜 스펙트럼 혹은 로그 멜 스펙트럼 등이 더 널리 쓰인다.

이미지 출처: Tan, Xu, et al(2021)

Code: MFCC

import librosa.display
fig, axes = plt.subplots(2)
wav, sr = librosa.load(librosa.ex("choice"), duration = 5)

S = librosa.feature.melspectrogram(wav, sr=sr, n_mels = 256)
log_S = librosa.power_to_db(S, ref=np.max)
mel_img = librosa.display.specshow(log_S, sr=sr, x_axis='time', y_axis='mel', ax = axes[0])
axes[0].set_title('Mel power sepctrogram')
fig.colorbar(mel_img, format='%+02.0f dB', ax = axes[0])

mfcc = librosa.feature.mfcc(S=librosa.power_to_db(mel_S), n_mfcc=13)
mfcc = mfcc.astype(np.float32)
plt.figure(figsize=(12,4))
mfcc_img = librosa.display.specshow(mfcc, ax = axes[1], x_axis='time')
fig.colorbar(mfcc_img, ax=axes[1])
axes[1].set_title('MFCC')
fig.set_size_inches(10, 8)
fig.tight_layout()
plt.show()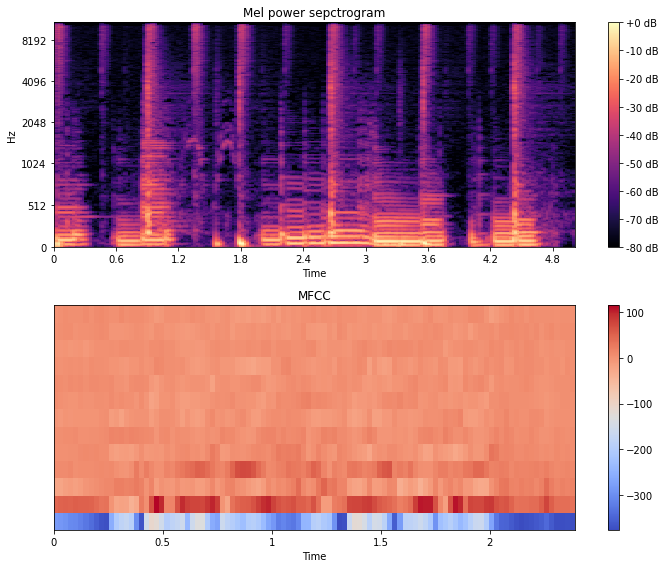

5. Data Preprocessing

5-1. Data Augmentation

  • Change Pitch
def change_pitch(data, sr):
    y_pitch = data.copy()
    bins_per_octave = 12
    pitch_pm = 2
    pitch_change = pitch_pm * 2 * (np.random.uniform())
    y_pitch = librosa.effects.pitch_shift(y_pitch.astype('float64'), sr, n_steps=pitch_change,
                                          bins_per_octave=bins_per_octave)
    return y_pitch
  • Change Amplitude
def value_aug(data):
    y_aug = data.copy()
    dyn_change = np.random.uniform(low=1.5, high=3)
    y_aug = y_aug * dyn_change
    return y_aug
  • Add Noise
def add_noise(data):
    noise = np.random.randn(len(data))
    data_noise = data + 0.005 * noise
    return data_noise
  • Decompose harmonic and percussive components
# 보통 harmonic part만 사용한다.
def hpss(data):
    y_harmonic, y_percussive = librosa.effects.hpss(data.astype('float64'))
    return y_harmonic, y_percussive
  • Shift
def shift(data):
    return np.roll(data, 1600)
  • Change Pitch & Speed
def change_pitch_and_speed(data):
    y_pitch_speed = data.copy()
    # you can change low and high here
    length_change = np.random.uniform(low=0.8, high=1)
    speed_fac = 1.0 / length_change
    tmp = np.interp(np.arange(0, len(y_pitch_speed), speed_fac), np.arange(0, len(y_pitch_speed)), y_pitch_speed)
    minlen = min(y_pitch_speed.shape[0], tmp.shape[0])
    y_pitch_speed *= 0
    y_pitch_speed[0:minlen] = tmp[0:minlen]
    return y_pitch_speed

Tip! use torch.nn.Sequential

train_audio_transforms = torch.nn.Sequential(
      torchaudio.transforms.MelSpectrogram(sample_rate=16000, n_mels=128),
      torchaudio.transforms.FrequencyMasking(freq_mask_param=15, iid_masks=False),  #freq_mask_param: masking의 크기	iid_masks: 배치마다 같은 마스킹을 줄것인가?
      torchaudio.transforms.TimeMasking(time_mask_param=35, iid_masks=False)
)

5-2. Filter

# btype: {‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’}
def butter_pass(cutoff, fs, btype, order=5):
    nyq = 0.5 * fs
    normal_cutoff = cutoff / nyq
    b, a = butter(order, normal_cutoff, btype=btype, analog=False)
    return b, a

def butter_filter(data, cutoff, fs, btype, order=5):
    b, a = butter_pass(cutoff, fs, btype, order=order)
    y = lfilter(b, a, data)
    return y

작성자: 15기 황보진경

References
출처의 검색일은 모두 2021.10.09.이다.

profile
Tobigs Sound Seminar
투빅스 15&16 음성세미나 입니다.

5개의 댓글

comment-user-thumbnail
이성범
2021년 10월 12일

[15기 이성범]
-질문-
멜 스펙트럼 방식과 퓨리에 변환은 서로 완전히 성질이 다른 방식인지? 아니면 서로 비슷한 방식인지 궁금합니다. 또 두 가지 방식을 함께 모델의 인풋으로 넣을 수 있나요?

-요약-

  • 음성의 주요 Task
    • Speech Classification
    • Auto-tagging
    • 음성인식(STT)
    • 음성합성(TTS)
    • 음성변환(STS)
  • 컴퓨터의 경우 연속적인 아날로그 신호(음성)을 Sampling, Quantizing, Encoding을 거쳐서 Binary Digital Signal로 변환하여 인식함
  • 인간의 경우 공기의 진동으로 음성을 인식함
    • 소리는 진동으로 인한 공기의 압축이고 압축이 얼마나 됬느냐가 wave, 즉 파동임
  • 소리는 다음과 같은 3개의 물리량을 가짐
    • Amplitude : 진폭 (높낮이)
    • Frequency : 주파수 (파동이 반복되는 주기)
    • Phase : 위상
  • 우리가 사용하는 대부분의 소리들은 복수의 서로 다른 정현파들의 합으로 이루어진 Complex wave 이다. 이게 무슨 말이냐면 우리가 보통 소리를 낼 때 도라는 동일한 음으로 이야기 하지 않을 것이다. 우리의 소리에는 다양한 음성이 합쳐져 있을 텐데, 도와 같은 음들은 동일한 파동을 가지는 주기 함수로 볼 수 있는데, 우리는 이러한 하나의 음을 낼때 이러한 서로 다른 동일한 파동을 가지는 주기 함수의 결합으로 하나의 음성이 표현된다고 볼 수 있다. 따라서 우리는 음성을 표현할 때 이러한 주기 함수들을 분해하는 것이 중요한 것이고, 이러한 주기 함수들을 분해하는 것이 바로 Fourier transform이라고 할 수 있다.
  • Fourier transform의 다양한 종류
    • Discrete Fourier Transform
    • Short Time Fourier Transform
    • ....
  • 이외에도 주파수 단위를 멜 단위로 바꾼, Mel-Filter bank / MFCC 등이 있다.

-자료-
https://hyunlee103.tistory.com/category/Audio%20%26%20Speech?page=3
음성에 대하여 잘 정리된 블로그임

답글 달기
comment-user-thumbnail
YMGYM
2021년 10월 13일

[15기 안민준]

  1. STFT 할 때 window 함수에 관한 질문입니다. window는 샘플링된 데이터의 amplitude의 Maximum을 나타낸다고 볼 수 있는건가요? 실제로 amplitude가 window값을 넘어가는 양 끝단 부분은 window 값 만큼만 취하고 STFT가 수행된다고 볼 수 있나요?
  2. Mel filter가 DFT된 데이터에 어떻게 적용되는지 구체적으로 알고 싶습니다. 1번처럼 특정 frequency 영역에서 임계값을 넘는 데이터를 제거한다고 볼 수 있을까요?
답글 달기
comment-user-thumbnail
‍조효원[ 학부재학 / 언어학과 ]
2021년 10월 13일

[15기 조효원]
MFCC에 대한 추가 설명 정리본
mfcc의 의미에 대해서 배운 바를 조금 설명을 하려고 합니다.

전통적인 패턴 매칭 방식은 음성의 특징 피쳐들을 추출하여, 이 패턴을 학습시켜 Recognition classifier를 학습시키곤 했는데, 이때 1980년 대 이후 특징을 추출하는 방법 중 가장 지배적인 방식이 MFCC입니다.

강의자료에도 정리되어있듯, 형태는 크게 waveform, Magnitude Spectrogram (by STFT), Mel Spectrogram (by Mel Filterbank), Log-Mel Spectrgoram, MFCC (by Discrete Cosine Transform) 순으로 바뀝니다.

보다 정확하게 설명하면,
1. pre-emphasis: 음성 신호의 고주파 성분 강조
2. windowing: frame이라 불리는 균일한 구간으로 분할해 오버랩시키며 분할
3. DFT: 음성 신호 -> 주파수 성분 변환
4. Mel filter bank: 사람의 귀는 모든 주파수 밴드에 균일하게 반응하지 않는다. 즉, 인간의 주파수 지각은 비선형적이다. 이러한 비선형적 주파수 지각을 모델링 한 것이 멜 필터 뱅크!
5. log: log를 통해 저주파와 고주파 스케일링 및 magnitude만 남기기
6. IDFT: cepstrum 만들기 => 스펙트럼의 log에 대해 다시 spectrum을 취하는 효과 => 이는 sound-source와 vocal tract 성분이 혼합되어 있는 스펙트럼에서 음성 인식에 필요한 vocal tract 성분만 취하는 효과를 가진다.

결과적으로 13개의 피쳐를 추출하는데, 이때 첫번째 값은 energy(주변 윈도우를 비교했을 때 변화율)이므로, 보통 버린다.

강의에서도 말해주셨 듯, 이제는 주되게 사용하진 않지만 여전히 고려되는 피쳐 중 하나이기에 정리해보았습니다! 사진으로 보면 더 명확하게 이해 가능합니다:)

답글 달기
comment-user-thumbnail
Taehee Kim
2021년 10월 13일

DFT변환과 DCT변환의 차이가 잘 이해가 안 가는데 DFT에서의 복소함수에서 코사인 부분만을 사용해 변환을 하는 것이라고 이해한 것이 맞을까요?
멜 스펙트럼/로그멜스펙트럼의 경우 데이터 양이 매우 큰 걸로 알고 있고 또 DFT도 N^2 의 연산이 필요한 것으로 알고 있는데 스펙트로그램을 DCT 변환하여 데이터의 양을 줄이는 것이 장기적으로 보았을 때 연산에 이득이 있는 것인지 궁금합니다.

1개의 답글