Index는 왜 B-Tree 계열을 사용할까

오늘처음해요·2024년 8월 30일

INDEX

첨부된 이미지를 활용하여 발표하듯 누군가에게 설명하면서 공부해보세요!

목표

이 글을 읽으시고 인덱스에 왜 B-Tree 계열을 쓰는지 알게 되셨으면 좋겠습니다.

Index 란?

인덱스는 데이터베이스에서 데이터를 빠르게 찾기 위해 특정 컬럼의 값을 기반으로 정렬된 데이터 구조입니다.
컬럼을 정렬해놓으면 어떻게 데이터를 빠르게 찾을 수 있는 지 알아봅시다!

Full Scan

인덱스를 만들 지 않은 컬럼에서 조회를 하면 순차적으로 모든 레코드 확인합니다.
아래의 경우처럼 Full Scan은 모든 레코드를 확인하여 O(N)만큼의 시간복잡도가 발생합니다.
다만 Full Scan이 무조건 안좋고, 인덱싱이 무조건 좋은 것은 아닙니다.

예외가 될 수 있는 경우는 다음과 같습니다.

조회하려는 데이터가 테이블의 상당 부분을 차지할 때
(카디널리티가 낮고, 데이터의 중복성이 높은 경우 )

테이블의 레코드 수가 적을 때 (수십~수백 건 사이인 경우)

자주 변경되는 테이블 (삽입, 삭제, 업데이트 마다 인덱스도 수정해줘야 함)

Binary Search Tree

이진 탐색 트리는 데이터가 삽입되는 과정에서 자동으로 정렬된 상태를 유지하기 때문에, 특정 값을 검색할 때 트리의 구조를 활용하여 평균적으로 O(log N)의 시간 복잡도를 가집니다.
따라서, 컬럼에 대해 이진 트리 구조를 활용한 인덱스를 생성하면, 검색 시 Full Scan보다 훨씬 효율적이며, 평균적으로 더 낮은 시간 복잡도로 원하는 데이터를 찾을 수 있습니다.

다만 이진 트리는 한 쪽으로 편향될 가능성이 있고, 편향될 경우 O(N)의 시간복잡도를 가집니다.
이를 보완하고자 최악의 경우에도 O(logN)의 시간복잡도를 가지는 균형을 맞춘 AVL Tree, Red-Black Tree도 존재합니다.

AVL Tree와 B-Tree도 O(logN)의 시간복잡도를 가지는데 왜 B-Tree 계열이 주로 인덱싱에 활용될까요?

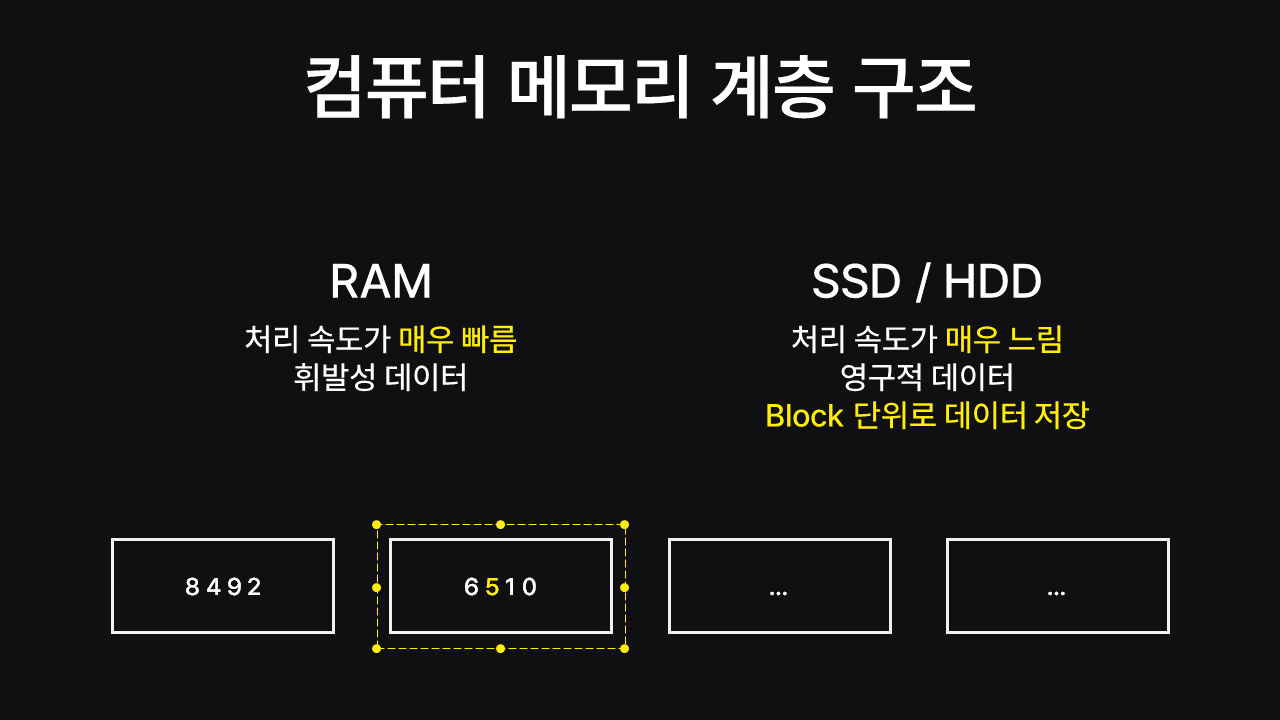
컴퓨터 메모리 계층 구조

DB의 데이터는 영구적으로 데이터가 보관되는 SSD/HDD에 보관됩니다. 대신 RAM에 비해 처리 속도가 매우 느리다는 특징이 있죠! RAM과 비교했을 때 대략적으로 SSD는 약 100배, HDD는 약 500배 차이난다고 생각하면 됩니다. 따라서 DB 성능의 최적화를 위해서는 메모리 IO의 횟수를 최대한 줄이는 것이 포인트입니다.

RAM DDR4 50GB/s, SSD SATA3 550MB/s, HDD 100MB/s 기준

SSD와 HDD에는 아래 그림과 같이 Block 단위로 데이터가 저장됩니다.
5라는 데이터를 꺼내고 싶어도 6 1 0처럼 사용안하는 블록의 데이터까지 전부 꺼내와야 합니다.
하지만 블록에 4 5 6 7과 같이 연관된 데이터가 저장되어 있다면 범위 탐색을 할 때 유용한 데이터들을 한꺼번에 꺼내올 수 있겠죠. 블록 안에 연관된 데이터가 저장되면 메모리 IO의 접근 효율성을 높일 수 있습니다!

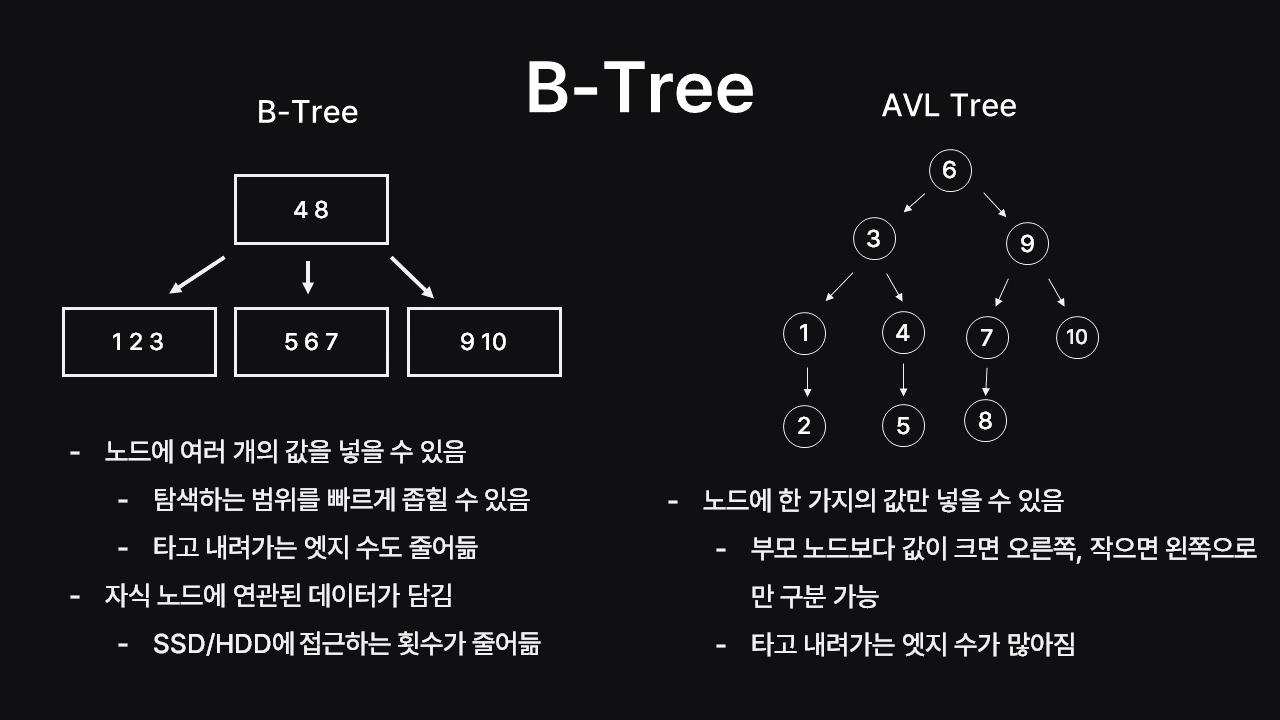
B-Tree

AVL Tree는 노드에 하나의 값만 넣을 수 있는 반면 B-Tree는 노드에 여러 개의 값을 넣을 수 있습니다. 예를 들어, B-Tree에서 2인 값을 찾는다고 하면 한 번의 계층 이동만으로 2/3의 범위를 줄이고 2를 찾을 수 있습니다. 반면, AVL Tree는 3번의 계층 이동이 필요하며 각각의 데이터가 다른 블록에 저장되어 있으면 필요없는 데이터까지 들어있는 블록들을 계속 꺼내와야 합니다.