[알고리즘 공부] 선택 정렬(Selection Sort)

김현정·2025년 3월 6일

CS 알고리즘 정렬

CS - 알고리즘

목록 보기

2/5

선택 정렬(Selection Sort)

선택 정렬은 해당 순서에 원소를 넣을 위치는 이미 정해져있고, 어떤 원소를 넣을지 선택하는 알고리즘이다. (거품 정렬과 유사한 알고리즘)

Process

주어진 배열 중에 최소값을 찾는다.
그 값을 맨 앞에 위치한 값과 교체한다(pass).
맨 처음 위치를 뺀 나머지 배열을 같은 방법으로 교체한다.

Java Code

void selectionSort(int[] arr) {
    int indexMin, temp;
    for (int i = 0; i < arr.length-1; i++) {        // 1.
        indexMin = i;
        for (int j = i + 1; j < arr.length; j++) {  // 2.
            if (arr[j] < arr[indexMin]) {           // 3.
                indexMin = j;
            }
        }
        // 4. swap(arr[indexMin], arr[i])
        temp = arr[indexMin];
        arr[indexMin] = arr[i];
        arr[i] = temp;
  }
  System.out.println(Arrays.toString(arr));
}

우선 위치(index)를 선택해준다.
i+1번째 원소부터 선택한 위치(index)의 값과 비교를 시작한다.
오름차순이므로 현재 선택한 자리에 있는 값보다 순회하고 있는 값이 작다면, 위치(index)를 갱신해준다.
'2'번 반복문이 끝난 뒤에는 indexMin에 '1'번에서 선택한 위치(index)에 들어가야하는 값의 위치(index)를 갖고 있으므로 서로 교환(swap)해준다.

Gif로 이해하기

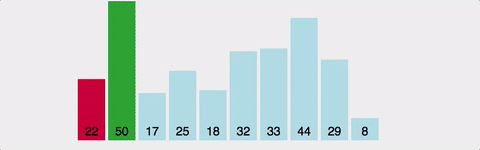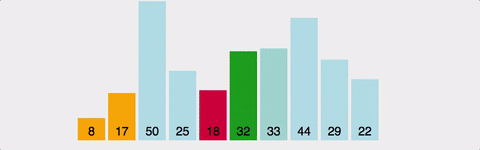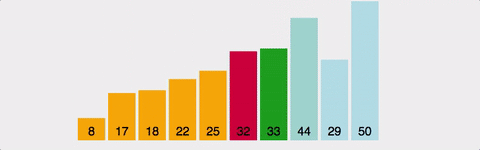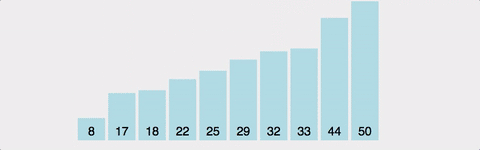
시간복잡도

데이터의 개수가 n개라고 했을 때,

첫 번째 회전에서의 비교횟수 : 1 ~ (n-1) => n-1
두 번째 회전에서의 비교횟수 : 2 ~ (n-1) => n-2
.....
(n-1) + (n-2) + ... + 2 + 1 => n(n-1)/2
비교하는 것이 상수 시간에 이루어진다는 가정 아래, n개의 주어진 배열을 정렬하는데 O(n^2)만큼의 시간이 걸린다. 최선, 평균, 최악의 경우 시간복잡도는 O(n^2)으로 동일하다.

공간복잡도

주어진 배열 안에서 교환(swap)을 통해, 정렬이 수행되므로 O(n)이다.

장점

거품 정렬과 마찬가지로 알고리즘이 단순하다.
정렬을 위한 비교 횟수는 많지만, 거품 정렬에 비해 실제로 교환하는 횟수는 적기 때문에 많은 교환이 일어나야 하는 자료상태에서 비교적 효율적이다.
거품 정렬과 마찬가지로 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않는다. => 제자리 정렬 (in-place sorting)