0. Overview
Recursive Algorithm의 복잡도 분석은 Iterative Algorithm에 비해 복잡합니다. 하지만, Recurrence Equation을 이용하면, 알고리즘의 시간복잡도를 쉽게 표현할 수 있습니다. 이번 글에서는 Recurrence Equation을 풀어, 최종 형태인 Closed Form을 구하는 대표적인 방법을 소개하겠습니다.
이번 글은 서강대학교 임종석 교수님의 강의와 Richard Neapolitan의「Foundation of Algorithm」을 참고하여 작성했음을 밝힙니다.
1. By Subsitution
Recurrence Equation의 Closed Form을 구하는 방법에는, by Induction, by Characteristic Equation, by Substitution등이 있는데, 이 중 가장 일반적으로 쓰이고, 손쉬운 방법은 Substitution을 이용하는 것입니다.
예시로, 일 때 에 대한 Closed Form 는, 다음의 과정을 통해
임을 알 수 있습니다.
![]()
2. Time Complexity
알고리즘의 Complexity Function은 보통 다음 네 가지 형태 중 하나의 모습을 하고 있습니다.
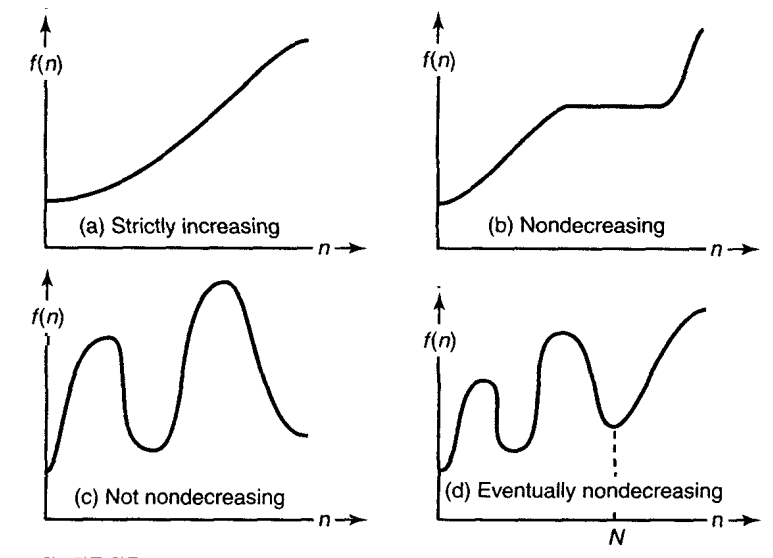
대부분 알고리즘의 시간(공간)복잡도는 Nondecreasing 알고리즘인데, 보통 input size가 커질수록 연산량이 많아져, 연산을 하는데 시간이 많이 걸리기 때문입니다.
하지만, 몇몇 알고리즘의 시간 복잡도는 Eventually nondecreasing 알고리즘인데, 이럴 경우 T(n)과 W(n)에 대한 Closed Form을 구하기 굉장히 어려운 경우가 많습니다. 이 때, Master Theorem을 이용해 정확한 Closed Form이 아닌 Bound를 구할 수 있습니다.
3. Master Theorem
Recursive Algorithm의 시간복잡도를 분석하면, 일반적으로 수식의 형태가
형태로 나옵니다.
이 때, Master Therorm은 다음과 같습니다.

