[DataStructure] Heap

이번 글은 서강대학교 소정민 교수님의 강의와 Ellis Horowitz의「Fundamentals of Data Structures in C」를 바탕으로 작성했음을 밝힙니다.

From Textbook

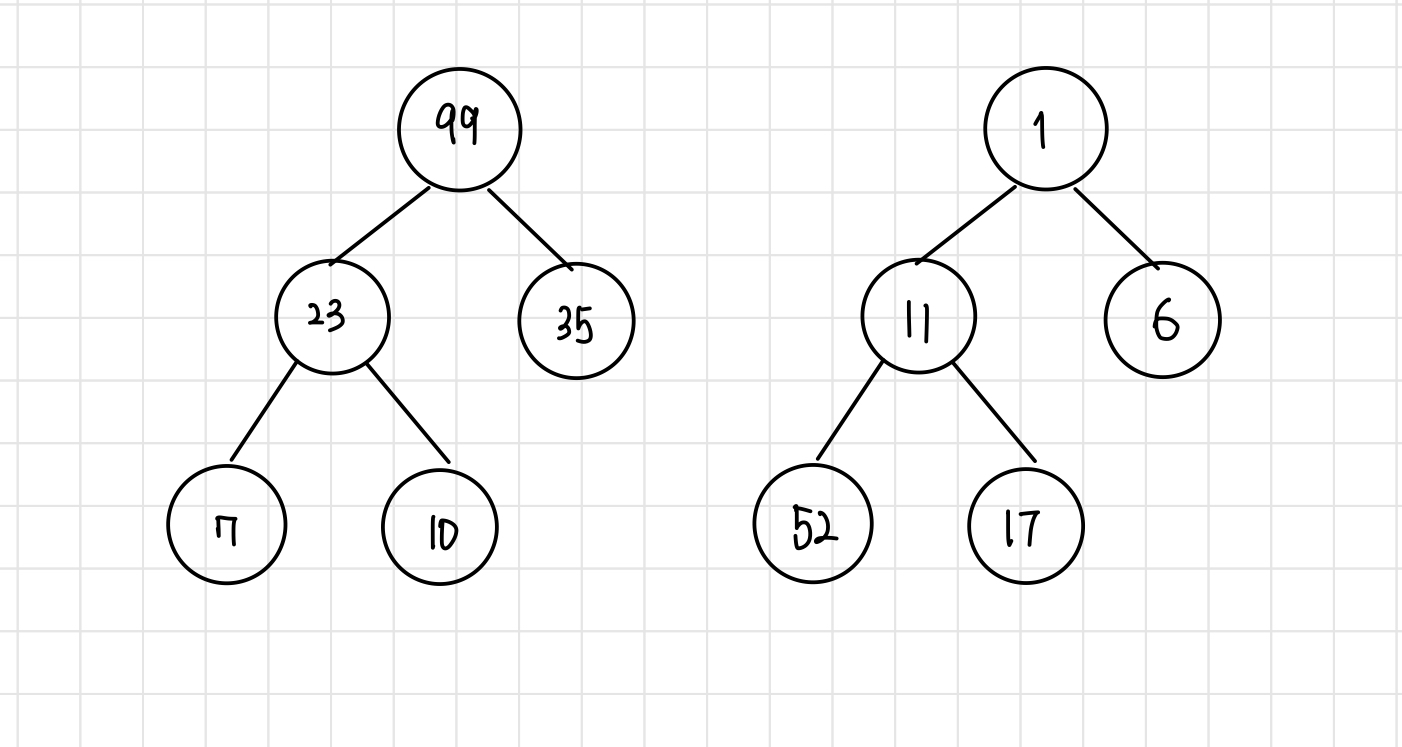
Heap is a special form of a complete binary tree that is used in many applications.

From Wiki

힙(Heap)은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리(complete binary tree)를 기본으로 한 자료구조로서, 다음과 같은 속성을 만족한다.

• A가 B의 부모 노드이면, A의 키값과 B의 키값 사이에는 대소관계가 성립한다.

힙에는 두 가지 종류가 있으며, 부모노드의 키값이 자식노드의 키값보다 항상 큰 힙을 최대 힙, 부모노드의 키값이 자식노드의 키값보다 작은 힙을 최소 힙 이라고 부른다.

1.1 ADT

Max Heap

• Definition : A max tree is a tree in which the key value in each node is no smaller than the key valuse in its children(if any). A max heap is a complete binary tree that is also a max tree.
• Operation: (1) creation of an empty heap (2) insertion of a new element into the heap (3) deletion of the largest element from the heap.

Min Heap

• Definition: A min tree is a tree in which the key value in each node is no larger than the key valuse in its childres(if any). A min heap is a complete binary tree that is also a min tree.

• Operation: (1) creation of an empty heap (2) insertion of a new element into the heap (3) deletion of the smallest element from the heap.

1.2 Priority Queue

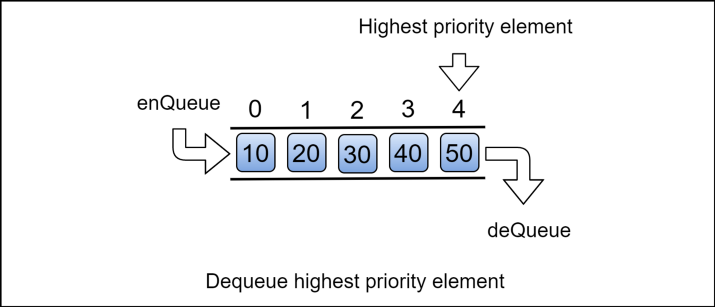
우선 순위 큐(Priority Queue)는 큐와는 다른 자료구조입니다. 큐는 FIFO, 즉 선착순으로 먼저 들어간 원소가 먼저 나오는 성질을 가지고 있지만, 우선 순위 큐는 어떤 원소가 먼저 enque 되었는지는 상관 없이 Priority 가 가장 높은(최대 혹은 최소) 원소가 먼저 pop 됩니다.

우선 순위 큐를 구현할 수 있는 방법은 여러 가지가 있습니다.

1.2.1 Array Representation

Unordered array

먼저, insertion을 할 때에는 그냥 넣고, deletion을 할 때에 탐색을 해서 무엇이 가장 높은 priority를 갖고 있는지 찾는 방법입니다. 이 경우 deletion을 할 때 탐색을 해야 하기 때문에, $n$을 array에 들어 있는 element의 갯수라고 할 때, insertion과 deletion의 complexity는 다음과 같습니다.

• insertion: $O(1)$
• deletion: $O(n)$

Ordered array

반대로, insertion할 때에 정렬을 해서 넣고, deletion을 할 때에 순서대로 뽑는 방법도 있는데, 이 경우 각각의 complexity는 다음과 같습니다.

• insertion: $O(n)$
• deletion: $O(1)$

즉, unordered array를 이용하면 Deletion에, ordered array를 이용하면 insertion에 강점이 있게 됩니다. 하지만, 현실의 여러 문제에서는 insertion과 deletion 중 어느 한 연산이 집중적으로 일어나는 경우는 거의 없습니다. 이 때, heap 자료구조를 이용하면 두 연산을 조금 더 빠른 시간에 할 수 있습니다.

1.3 Heap representation

insertion

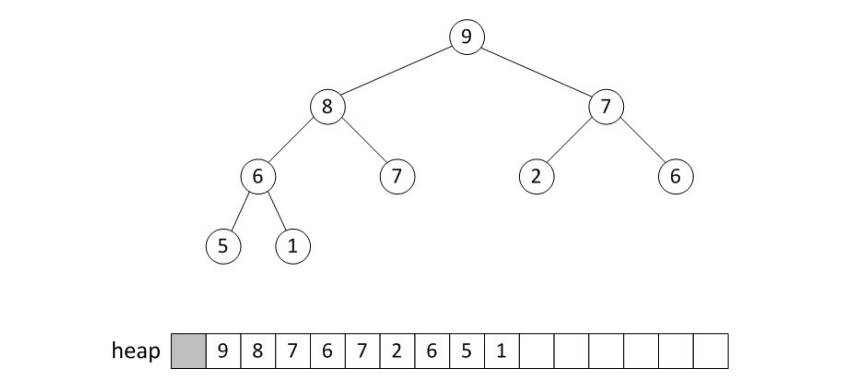
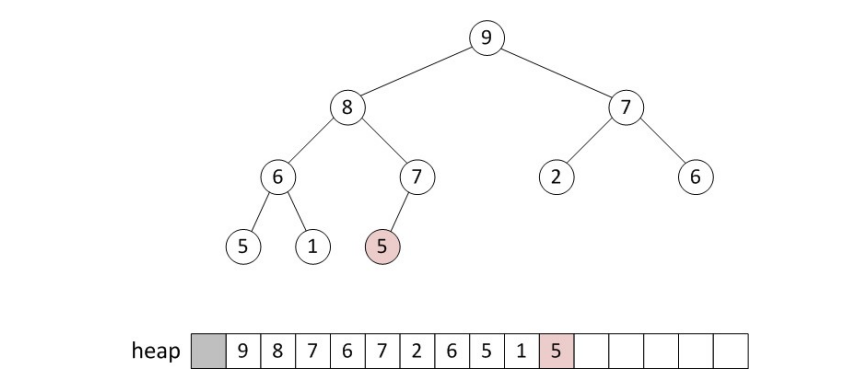
먼저 새로운 공간에 element를 위치시킵니다. 그 다음에 parent node와 값을 비교해 더 크다면(min tree의 경우 더 작다면) parent node와 교체합니다.

이 연산은 root node에 도달하거나, parent node의 값이 자신의 값보다 더 클 때까지(더 작을 때까지) 반복합니다.

deletion

Heap에서 deletion은 항상 root node에서 수행됩니다. 따라서, deletion 이 수행되고 나면 root node가 비어있는 상태가 되는데요. 이 때 일단 순서상 마지막에 있는 node를 root node의 자리로 끌어와 tree의 를 유지시킵니다.

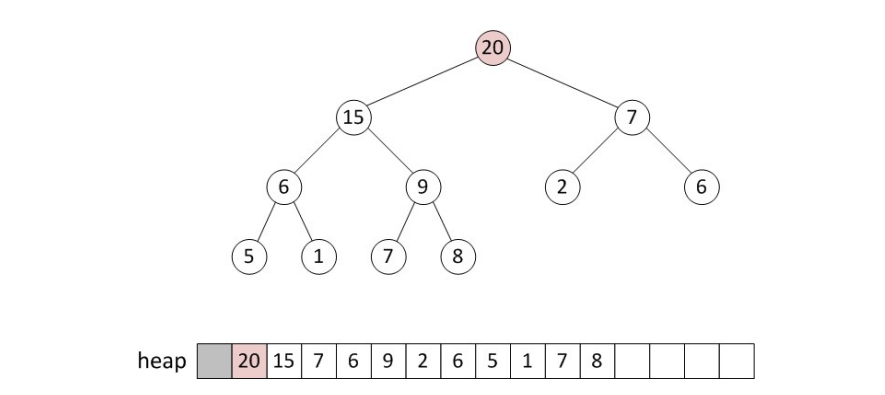
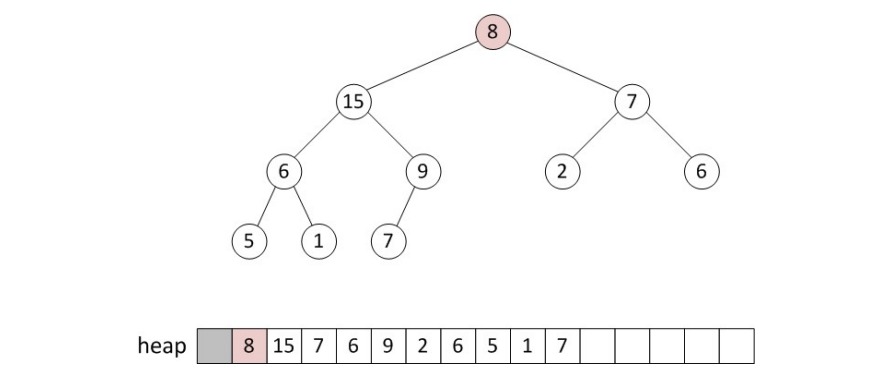
그 다음에, root node와 child node를 비교해 더 큰 (min tree의 경우 더 작은) 값이 존재한다면 교채해줍니다.

이 연산은 leaf node에 도달하거나, child node의 값이 자신의 값보다 더 작을 때까지(더 클 때까지) 반복합니다.

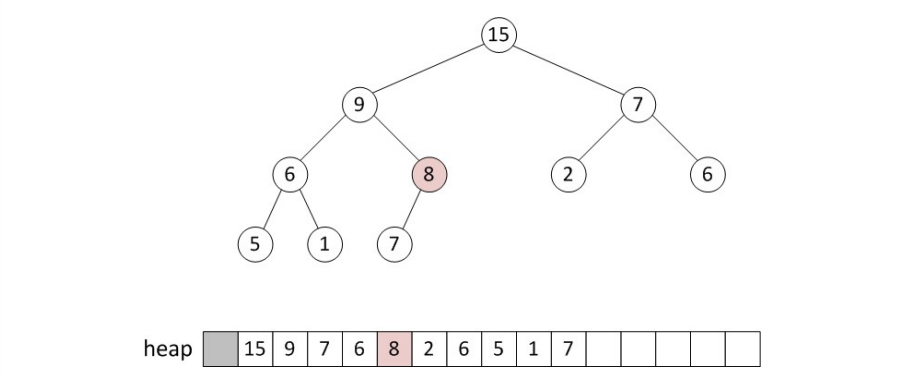
Time Complexity

Heap으로 insertion 연산과 deletion 연산을 수행하는 데 있어서 최악의 상황은 root부터 leaf까지 바꾸는 연산을 모두 수행하는 것입니다.

n개의 node를 가진 완전이진트리의 depth는 $log_2{n+1}-1$이고, 따라서 이 경우의 complexity는 $O(logn)$이 됩니다.

1.2.2 Complexity Summary

Representation	Insertion	Deletion
unordered array	$O(1)$	$O(n)$
unordered linked list	$O(1)$	$O(n)$
sorted array	$O(n)$	$O(1)$
sorted linked list	$O(n)$	$O(1)$
max heap	$O(logn)$	$O(logn)$