[Algorithm] 이코테 - 1로 만들기

◽️ 1로 만들기

문제설명

정수 X가 주어질 때 정수 X에 사용할 수 있는 연산은 다음과 같이 4가지 이다.

ⓐ X가 5로 나누어 떨어지면 5로 나눈다.
ⓑ X가 3으로 나누어 떨어지면 3으로 나눈다.
ⓒ X가 2로 나누어 떨어지면 2로 나눈다.
ⓓ X에서 1을 뺀다.

정수가 주어졌을 때, 연산 4개를 적절히 사용해서 1을 만들려고 한다. 연산을 사용하는 횟수의 최솟값을 출력하시오

입력조건

첫째 줄에 정수 X가 주어진다.(1 <= X <= 30,000)

출력조건

첫째 줄에 연산을 하는 횟수의 최솟값을 출력한다.

풀이

DP 문제라는 걸 알고 있었는데도 불구하고 DP에 대한 이해도가 낮아서 그런지 풀기가 굉장히 어려웠다.

책에서 권장하는 풀이 시간은 20분인데 그 안에 풀지 못해서, 솔루션을 먼저 보고 다시 푸는 형식으로 진행했다. 사실 풀이보고도 바로 이해하진 못했다...ㅎ^^ 이게 난이도가 낮은 문제라니..~~

• 네가지 연산을 통해서 정수 X를 1로 만드는 데 걸리는 최소 횟수를 저장할 DP 배열을 만든다.
  • D[1] = 0
    이미 1이기에 연산할 필요가 없다.
  • D[2] = 1
    -1을 하거나, 2로 나눈다.
  • D[3] = 1
    3으로 나눈다.
  • 이렇게 바텀업 방식으로 각 정수가 1을 만드는 데 걸리는 최소 횟수를 저장하면 된다.

• 2, 3, 5로 나누어지는 경우는 당연히 연산 횟수가 1이다.
  그런데 수가 나누어 떨어지지 않은 경우에는 어떻게 구해야 하는지가 헷갈렸다.
  • 바텀업 방식이기 때문에 D[x-1]에는 정수 x-1을 1로 만드는 최소 횟수를 이미 계산해둔 상태이다.
    따라서 정수 x에서 1을 빼서 정수 x-1을 만들면 된다(연산 1회 추가)
    즉, D[x-1] + 1 가 최소횟수가 된다.

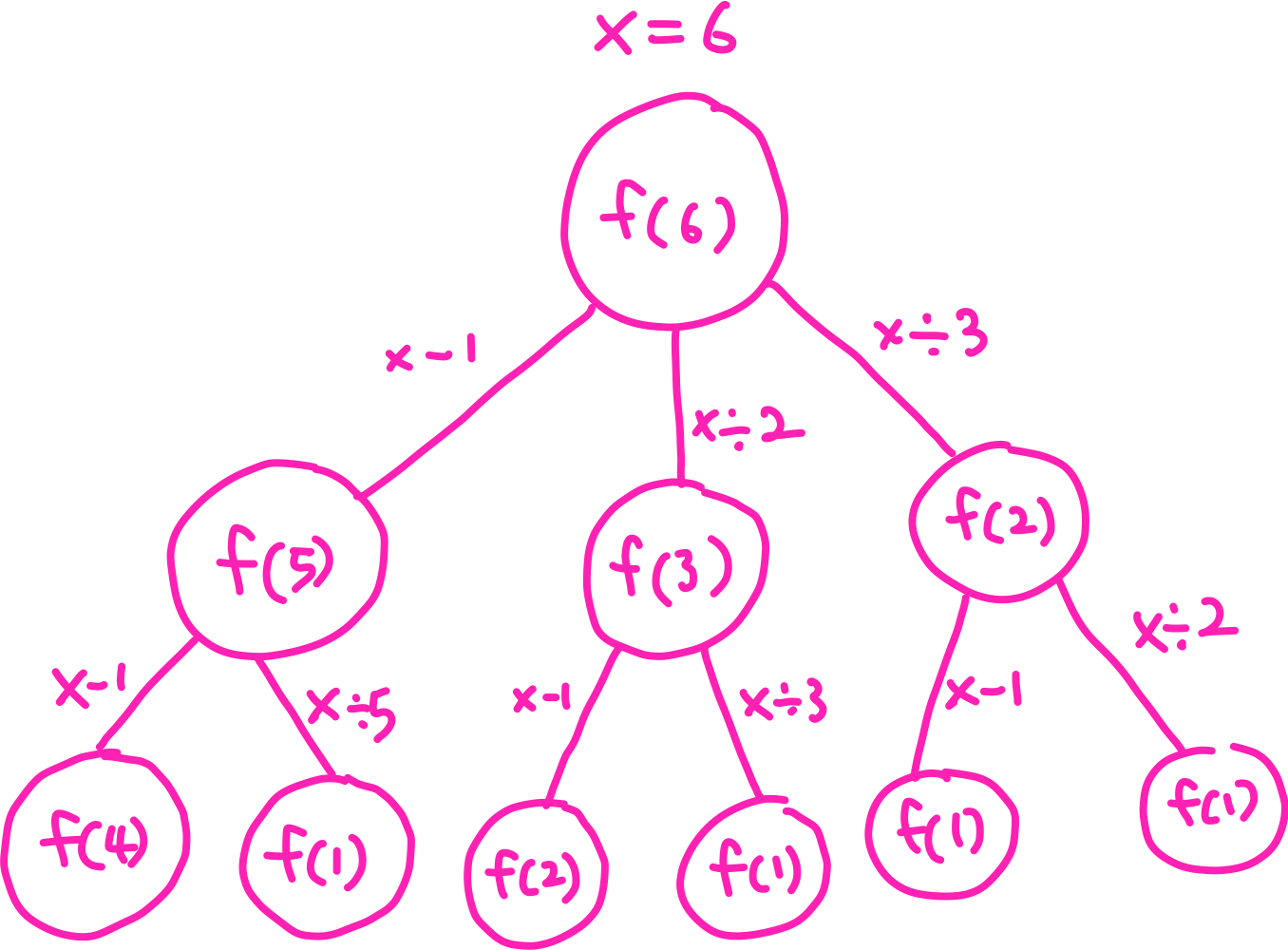
X = 6일 때, 피보나치 수열처럼 재귀적으로 구현한다고 했을 때처럼 함수과 호출되는 과정을 도식화 하면 아래와 같다.
바텀 업 방식으로 구현했기에 맨 아래 f(1)부터 f(6)을 구해나간다고 생각하면 될 것 같다.

Solution

x = int(input())
d = [0] * (x+1)

for i in range(2, x+1):
    d[i] = d[i-1] + 1
    if i % 2 == 0:
        d[i] = min(d[i // 2] + 1, d[i])
    if i % 3 == 0:
        d[i] = min(d[i // 3] + 1, d[i])
    if i % 5 == 0:
        d[i] = min(d[i // 5] + 1, d[i])

print(d[x])

책에서는 dp 테이블을 정수 범위인 30000에 맞춰서 초기화해주는데, 나는 입력되는 정수에 맞춰 테이블 크기를 초기화해주었다!