유니온 파인드(disjoint-set)

분리 집합, 서로소 또는 상호 배타조합, 유니온 파인드, disjoint - set 이라고 표현하는 집합들은 서로 중복 포함된 원소가 없는 즉 교집합이 없는 집합입니다.

집합에 속한 하나의 특정 멤버를 식별자로하여 각 집합을 구분합니다. 이를 대표자라고 합니다.

분리 집합은 연결리스트 혹은 트리로 구현하며 Make-Set, Find-Set, Union 알고리즘으로 집합 간 연산을 수행합니다.

• Make-Set (x)
  • 유일한 멤버 x를 갖는 새로운 집합을 생성
• Find-Set (x)
  • x를 포함하는 집합의 대표자를 찾아서 반환
• Union (x, y): 집합 엮기
  • 두 집합의 부모를 FindSet을 통해서 찾은 뒤 y의 부모를 x 로 설정

연결리스트 구현

같은 집합의 원소들은 하나의 연결리스트로 관리합니다. 또한 연결리스트의 맨 앞 원소를 집합의 대표원소로 사용하며 각 원소는 집합 대표원소를 링킹합니다.

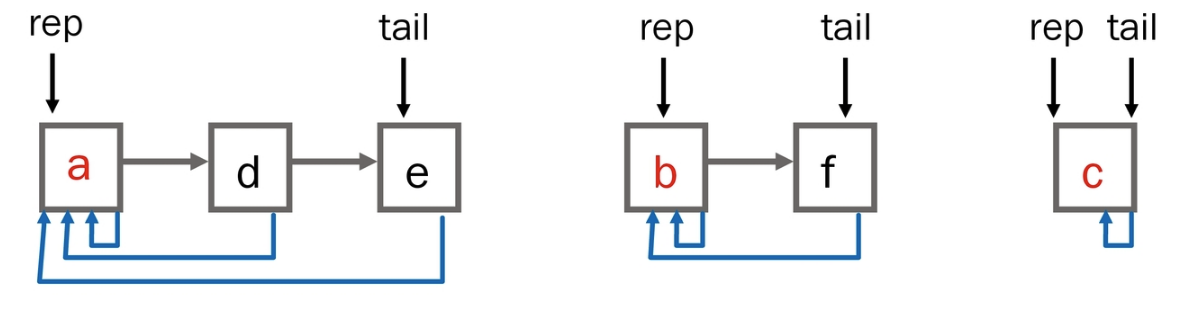
연결리스트는 사용하는 노드만 데이터로 저장하기에 구현에 난이도가 있지만 공간복잡도가 비교적 낮습니다.

연결리스트 유니온-파인드 연산

각 분리 집합을 원하는 집합에 연결합니다. 그 후 합쳐진 리스트의 원소들이 하나의 대표원소를 링크하게 합니다.

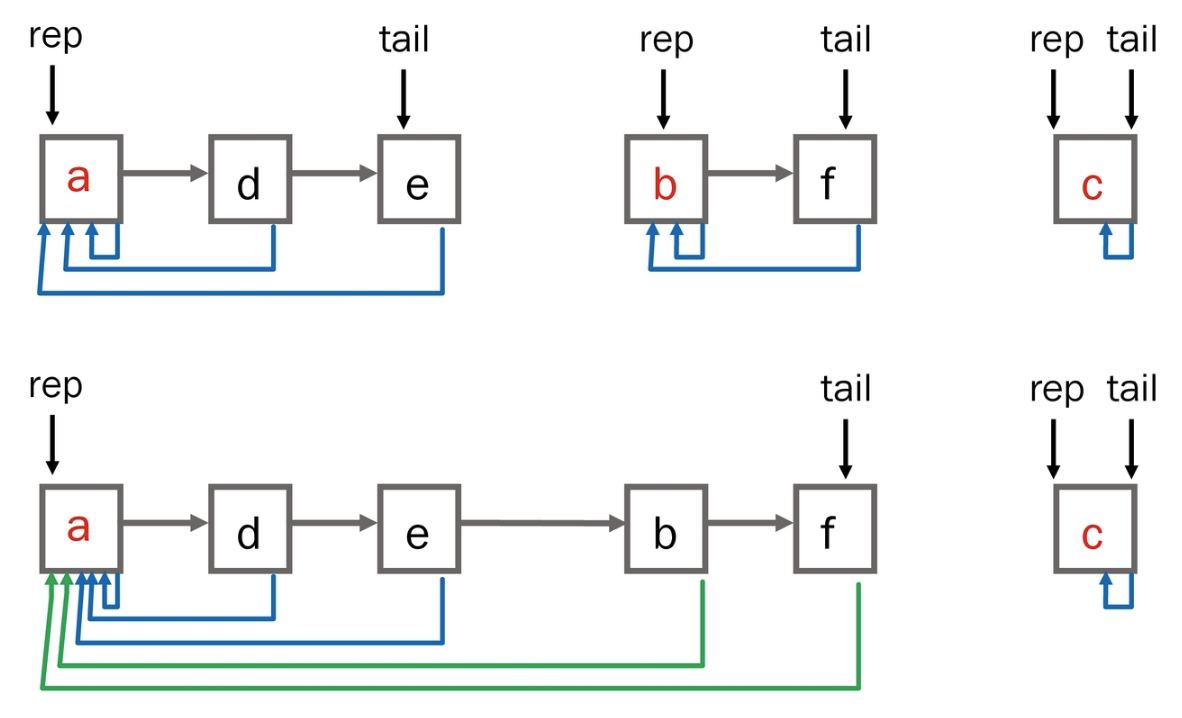
트리 구현

하나의 집합을 하나의 트리로 표현하여 구현합니다. 루트노드를 대표자로 하며 루트 포함 집합의 모든 원소는 모두 루트를 부모로 합니다.

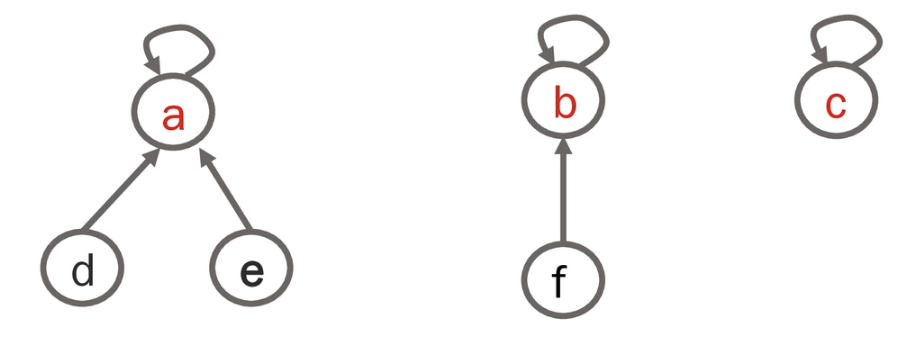
트리를 통한 유니온 파인드는 보통 배열로 구현하며 인덱스에 자신의 값을 저장하고 실제 값으로 부모를 가르킵니다. 이렇게 구현 시 필요없는 공간도 배열로 할당해야하므로 공간복잡도가 높지만 구현이 간단합니다.

트리 유니온 - 파인드 연산

각 트리를 유니온 연산 시 해당 트리의 루트가 합쳐질 트리의 루트를 참조하게 합니다.

Rank를 이용한 유니온 연산

해당 집합의 depth를 계산하여 부모 루트가 depth를 갖게 합니다. 유니온 연산 시 depth를 갱신합니다.

• 각 정점은 자신을 루트로하는 subtree의 높이를 저장
• 두 집합을 합칠 때 rank가 낮은 집합을 rank가 높은 집합에 붙임

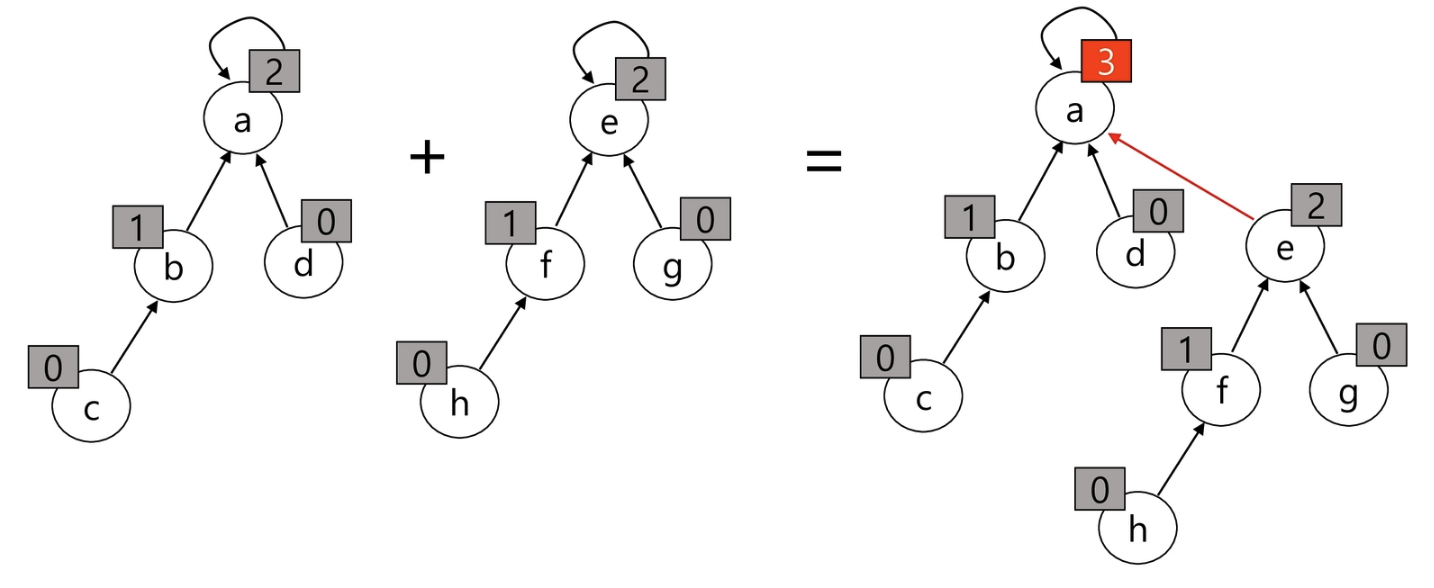
Path compression

Find-Set을 행하는 과정에서 만나는 모든 정점들이 직접 root를 가르키도록(root의 자식이 되도록) 바꿉니다.

Make

private void make(int size){
    for(int i = 0 ; i < size; i++){
        parents[i] = i;
    }
}

각 배열의 인덱스를 자신의 값으로 갖는 원소들의 부모를 자기자신으로 설정합니다.

Find

public int find(int x){
    if(parents[x] == x)    return x;
    //path compression 을 위해 parent[x] 값 갱신
    return parents[x] = find(parents[x]);
}

자기 자신이 부모인 값을 찾을 때까지 부모로 계속 재귀합니다. 반환값을 자신의 부모로 받아 Path compression 을 구현합니다.

union

public boolean union(int x, int y){
    int parX = find(x);
    int parY = find(y);
    if(parX == parY)    return false;
    parents[parY] = parX;
    return true;
}

각 원소의 부모를 찾고 두 원소의 부모가 같다면 이미 유니온 되어있다는 뜻으로 false 를 반환합니다. 아니라면 y 의 부모를 x 로 설정합니다.