정렬이란?
정렬은 특정 값을 기준으로 데이터를 순서대로 배치하는 작업입니다.
정렬의 종류
- 구현 난이도는 쉽지만, 속도는 느린 알고리즘
- 버블 정렬
- 삽입정렬
- 선택정렬
- 구현 난이도는 어렵지만, 속도는 빠른 알고리즘
- 합병정렬
- 힙정렬
- 퀵정렬
- 트리정렬
- 하이브리드 정렬
- 팀 정렬
- 블록 병합 정렬
- 인트로 정렬
- 기타정렬 알고리즘
- 기수 정렬
- 카운팅 정렬
- 셸 정렬
- 보고 정렬
구현 난이도는 쉽지만, 속도는 느린 알고리즘(버블, 삽입, 선택)
버블 정렬
버블 정렬은 인접한 데이터를 비교하여 자리를 바꾸는 방식이며, 알고리즘 복잡도는
O(n^2)입니다.
배열의 길이가 N이라고 가정하면
인덱스 0 ~ N까지 한번 순회하면 제일 큰 숫자가 맨 뒤에
존재하게 됩니다.
따라서 0 ~ N --> 0 ~ N-1 --> 0 ~ N-2 --> ... --> 0 ~ 1
까지 반복작업을 합니다.
삽입 정렬
앞의 데이터를 정렬하며 삽입 위치를 찾아 정렬합니다.
알고리즘 복잡도는O(n^2)입니다.
배열의 길이가 n 일 경우 1부터 시작하여 왼쪽과 비교합니다.
- 왼쪽보다 클 경우 오른쪽으로 넘어가서
1, 2를 비교합니다. - 왼쪽보다 작을 경우는
현재비교 수를현재비교 수 - 1과 자리를 변경합니다.
선택 정렬
최소 또는 최대 값을 찾아서 가장 앞 또는 뒤부터 정렬하는 방식입니다.
알고리즘 복잡도는O(n^2)입니다.
- 아래는 정렬을 구현한 코드입니다.
package chap5_algorithm.al_06_sort;
// 버블 정렬, 삽입 정렬, 선택 정렬
import java.util.Arrays;
public class Prac1 {
// 버블 정렬
public static void bubbleSort(int[] arr) {
for (int i = 1; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - i; j++) {
if (arr[j] > arr[j + 1]) {
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
}
}
// 삽입 정렬
public static void insertionSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
for (int j = i; j > 0; j--) {
if (arr[j - 1] > arr[j]) {
int tmp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = tmp;
} else {
break;
}
}
}
}
// 선택 정렬
public static void selectionSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int min = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
int tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
}
}
public static void main(String[] args) {
int[] arr = {3,5,2,7,1,4};
bubbleSort(arr);
System.out.println(Arrays.toString(arr));
arr = new int[]{3,5,2,7,1,4};
insertionSort(arr);
System.out.println(Arrays.toString(arr));
arr = new int[]{3,5,2,7,1,4};
selectionSort(arr);
System.out.println(Arrays.toString(arr));
}
}
구현 난이도는 어렵지만, 속도는 빠른 알고리즘 (합병, 퀵, 트리)
합병 정렬
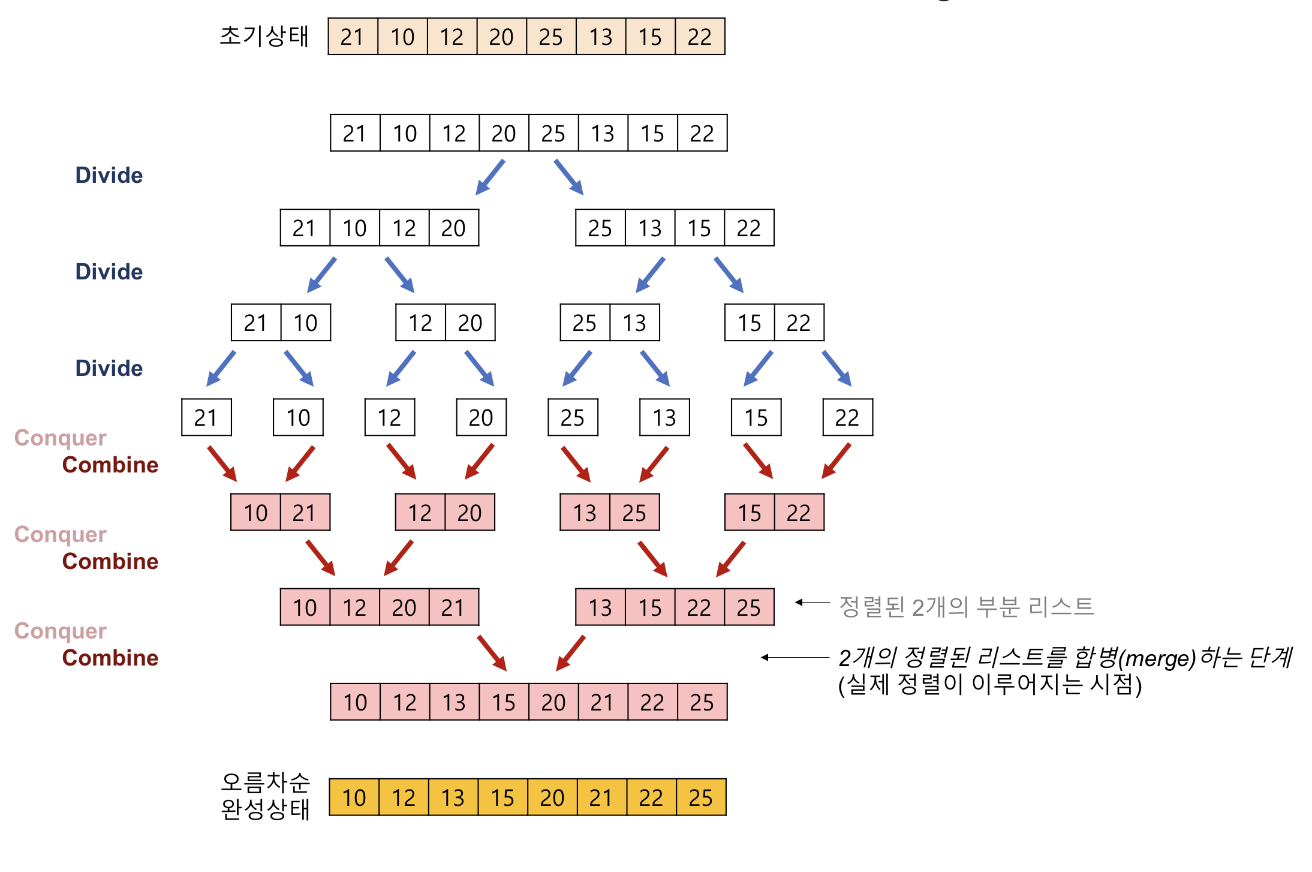
배열을 계속 분할해서 길이가 1이 되도록 만들고,
인접한 부분끼리 정렬하면서 합병하는 방식입니다.
알고리즘 복잡도는O(nlogn)입니다.
public static void mergeSort(int[] arr, int[] tmp, int left, int right){
if (left < right) {
int mid = (left + right) / 2;
mergeSort(arr, tmp, left, mid);
mergeSort(arr, tmp, mid + 1, right);
merge(arr, tmp, left, right, mid);
}
}
public static void merge(int[] arr, int[] tmp, int left, int right, int mid) {
int p = left;
int q = mid + 1;
int idx = p;
// 유효 범위인지 확인
while (p <= mid || q <= right) {
if (p <= mid && q <= right) {
if (arr[p] <= arr[q]) {
tmp[idx++] = arr[p++];
} else {
tmp[idx++] = arr[q++];
}
} else if (p <= mid && q > right) {
tmp[idx++] = arr[p++];
} else {
tmp[idx++] = arr[q++];
}
}
for (int i = left; i <= right; i++) {
arr[i] = tmp[i];
}
}퀵 정렬
임의의 기준 값(pivot) 을 정하고 그 값을 기준으로 좌우로 분할하며 정렬하는 방식 입니다.
알고리즘 복잡도는O(n^2)입니다.
버블, 삽입, 선택을 사용하면 되지 왜 퀵정렬을 사용해야 하는가? 의문이
들 수 있습니다.
시간 복잡도는 워스트 케이스이기 때문에 같은 시간 복잡도를 지니지만
실제로 퀵정렬은 굉장히 빠른 정렬 기법입니다.
워스트 케이스를 피하기 위해서 중요한 것은 pivot을 잘 선택하는 것입니다.
pivot 이 최솟값 혹은 최댓값인 경우 워스트 케이스가 발생합니다.
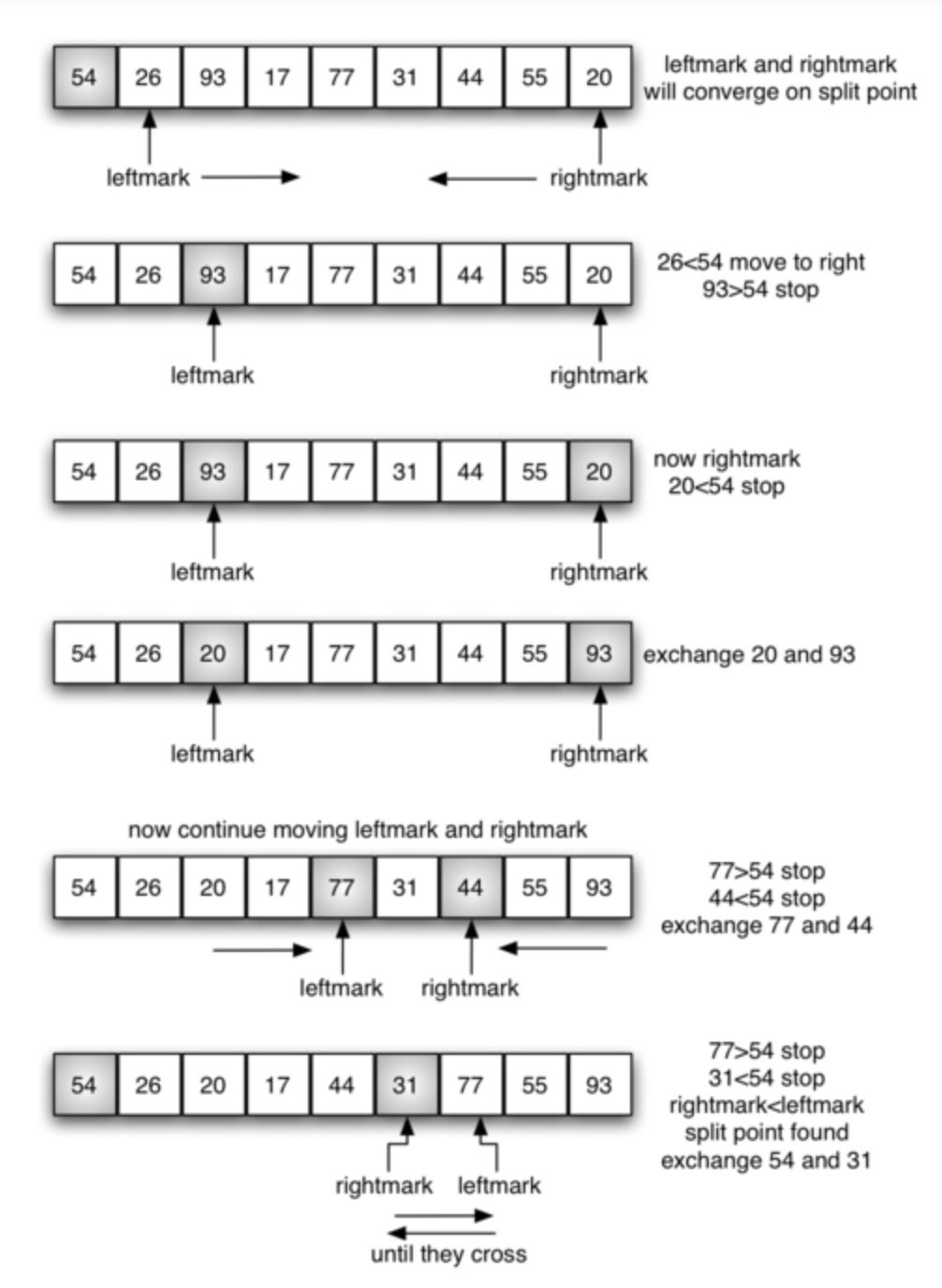
위의 사진을 봅시다. 인덱스 0의 값인 54를 기준으로 합니다.
바로 오른쪽을 leftmark, 맨 오른쪽을 rightmark로 지정합니다. leftmark가 기준보다 크고, rightmark가 기준보다 작을때 leftmark와 rightmark의 값을 교체합니다.
이러한 과정을 leftmark와 rightmark가 같은 인덱스에 위치할때까지 계속 진행합니다.
마지막으로 같은 인덱스에 기준 값인 54를 위치 시킵니다.
- 위의 작업이 끝나면 아래와 같은 작업이 진행됩니다.
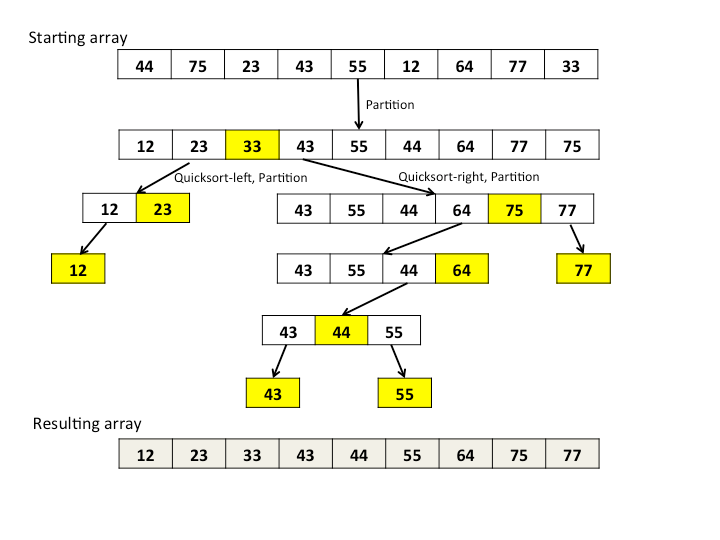
노란색으로 칠해진 33이 기준 인덱스가 위의 작업을 통해 자리를 변경한 거라고 생각해보겠습니다.
자리를 잡은 인덱스를 제외하고 왼쪽, 오른쪽을 분리하여 같은 작업을 반복하면 정렬이 완성됩니다.
public static void quickSort(int[] arr, int left, int right) {
if (left >= right) {
return;
}
int pivot = partition(arr, left, right);
quickSort(arr, left, pivot - 1);
quickSort(arr, pivot + 1, right);
}
public static int partition(int[] arr, int left, int right) {
int pivot = arr[left];
int i = left;
int j = right;
while (i < j) {
while (arr[j] > pivot && i < j) {
j--;
}
while (arr[i] <= pivot && i < j) {
i++;
}
swap(arr, i, j);
}
swap(arr, left, i);
return i;
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}트리 정렬
이진 탐색 트리(BST)를 만들어 정렬하는 방식입니다. 알고리즘 복잡도는 o(nlogn) 입니다.
기타 정렬 (기수, 계수)
기수 정렬
- 낮은 자리 수부터 정렬하는 방식입니다.
- 각 원소 간 비교 연산을 하지 않아 빠른 대신, 기수 테이블을 위한 메모리가 필요합니다.
- 알고리즘 복잡도는
O(dn)입니다. (d 는 최대 자릿수)
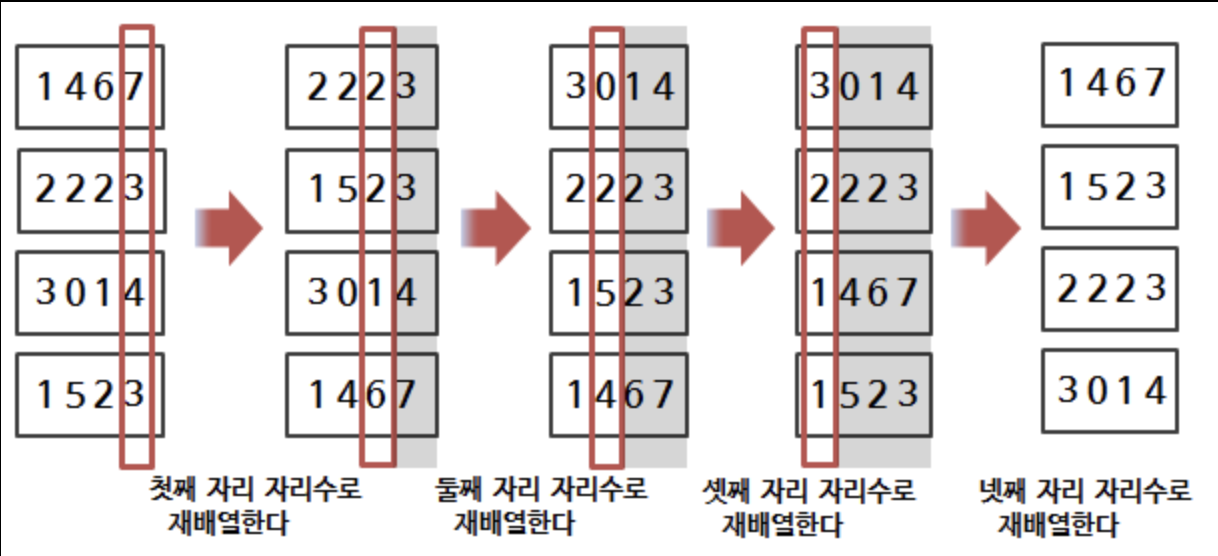
우선 1의 자리수를 비교하고, 10의 자리수, 1000의 자리수를 비교하는 방식입니다.
계수 정렬
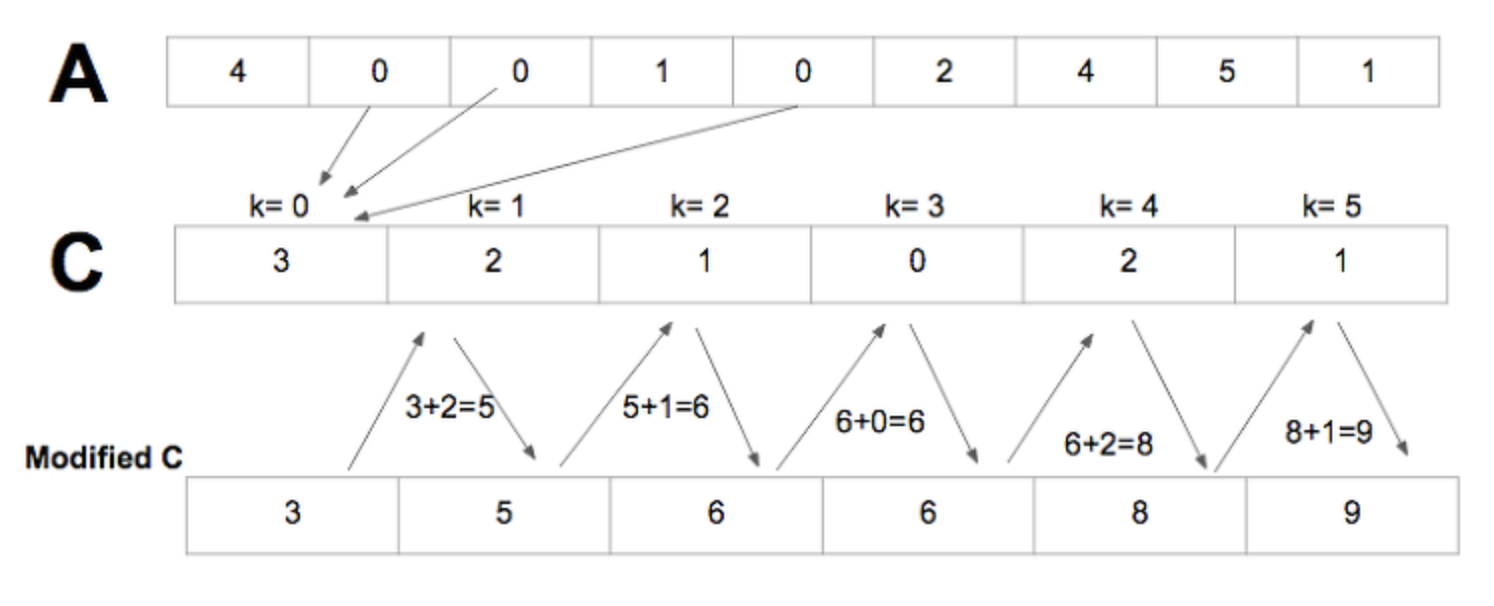
- 숫자끼리 비교하지 않고 카운팅을 하여 정렬하는 방식입니다.
- 카운팅을 위한 메모리 필요합니다.
- 알고리즘 복잡도
O(n + k)
셸 정렬
간격을 두어 삽입 정렬을 하는 것
삽입 정렬의 약점 보완한 정렬 방식입니다.- 이전의 모든 데이터와 비교하는 것이 아닌 일정 간격을 두어 비교합니다.
- 알고리즘 복잡도는
O(n^2)입니다.
간격을 어떻게 설정하는지가 중요합니다.
