다이내믹 프로그래밍 (Dynamic Programming)

다이내믹 프로그래밍이란??

하나의 문제를 단 한 번만 풀도록 하는 알고리즘이다.

피보나치 수열을 한번 봐보자

피보나치 수열은 특정한 숫자를 구하기 위해 그 앞에 있는 숫자와 두 칸 앞에 있는 숫자의 합을 구해야 한다.

• 피보나치 수열의 점화식: D[i] = D[i-1] + D[i-2]

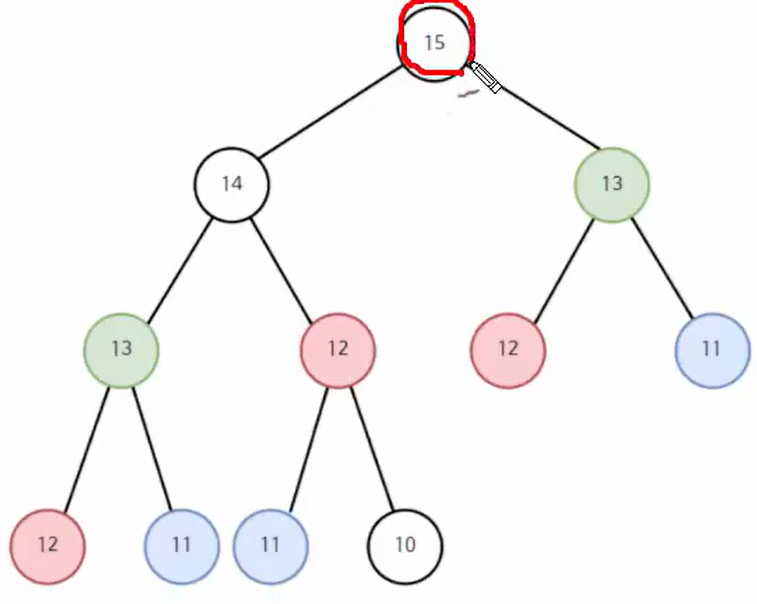
이 D[15]을 구하기 위한 과정을 보자.
D[15]을 구하려면 D[14]와 D[13]을 알아야 한다.
또 D[14]는 D[13]과 D[12]을 알아야 한다.
이런식으로 진행 되다 보면 그림에 보이는 것 처럼 D[12]의 값을 여러번 구하는 문제가 발생한다.
이미 해결한 문제를 다시 반복적으로 해결하여 비효율적이다.

다이내믹 프로그래밍은 다음의 가정 하에 사용할 수 있다.

1. 큰 문제를 작은 문제로 나눌 수 있다.
2. 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다.

즉, 쉽게 말해 크고 어려운 문제를 작게 나누어 해결한다. 작게 나뉘어진 답들은 배열에 저장한다. 이후 작게 나뉘어진 답들을 합쳐서 큰 문제를 해결한다. 이때, 이미 계산한 결과는 배열에 저장되어 있으므로 효율적이다.

단순 재귀 코드

static int fibo(int x) {
		if( x ==1 || x==2) return 1;
		return fibo(x-1) + fibo(x-2);
	}

단순 재귀 코드에서는 중복 호출을 하기 때문에 시간 복잡도가 O(2^n) 이다.

Top-down(하향식) 코드

상위 문제를 해결하기 위해서 하위 문제를 재귀적으로 호출하여 해결하는 방법이다.
이때 배열에 계산한 값을 저장한다.

static int fibo(int x) {
		if( x ==1 || x==2) return 1;
		if(dp[x] != 0) return dp[x];
		dp[x] = fibo(x-1) + fibo(x-2);
		return dp[x];
	}

Bottom-up(상향식) 코드

하위 문제에서부터 문제를 해결해나가면서 상위 문제를 해결해나가는 방식이다.
DP의 전형적인 형태이다.

static int fibo(int x) {
		dp[1] =1;
		dp[2] =1;
		for(int i=3; i<x+1; i++) {
			dp[i] = dp[i-1] + dp[i-2];
		}
		return dp[x];
	}