트리

선형 자료구조

선형 자료구조 : 배열, 연결 리스트, 스택, 큐

• 리스트형 자료구조
• 선형 자료 구조
• 모든 원소는 인덱스에 대응된다.

선형 자료구조의 한계점

모든 원소들 사이에서 관계 비교를 정하기 힘들다.

예를 들어

list = [8,19,20,25,36]

위 리스트는 내림차순으로 정렬되어 있습니다. 자신보다 크거나 작다는 관계를 공통적으로 가지고 있어 이 때는 선형 자료구조를 사용하기 좋습니다.

list = ['아들', '아빠', '엄마']

위 리스트에서는 아들과 아빠는 부자관계이고 아빠와 엄마는 부부관계인데 이렇게 2개 이상의 관계를 표현하는데 한계가 있습니다.

그림으로 표현해보면

이렇게 관계를 표현하는 것보다

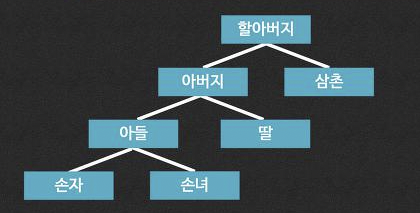
이렇게 보는게 훨신 보기 편하다고 생각할 것 입니다.

트리 구조

예시

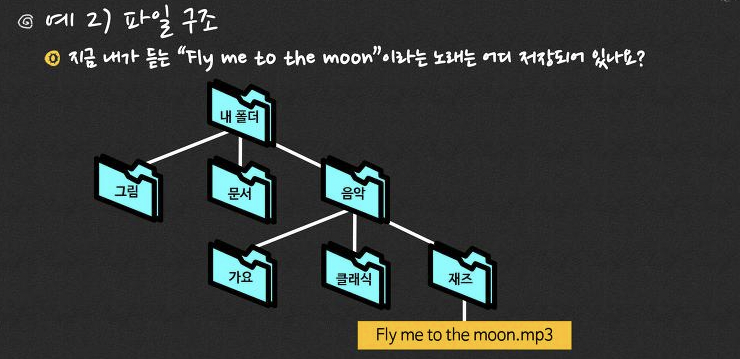
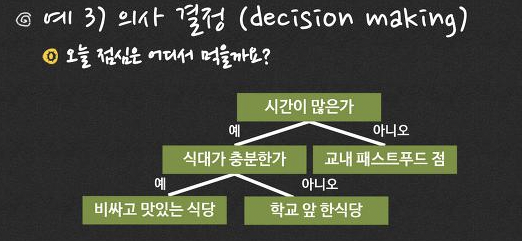
위 예시의 공통점

• 하나의 근원 (root)으로 부터 파생됨
• 한 노드가 여러 개의 노드로 전파됨
• 순환하는 경로 (cycle path)가 없음

트리의 정의

• 루트라는 특별한 노드가 하나 있다.
• 모든 노드는 부모 자식 관계라는 1:1 관계에 재귀적으로 연결되어 있다.
• 순환하는 경로 즉 한 번 내려갔으면 다시 올라오는 길이 없다.
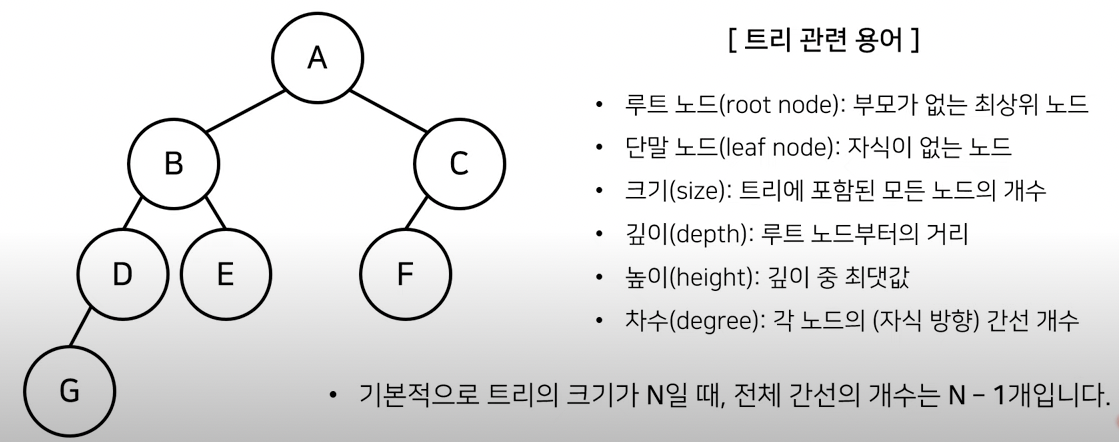  루트 노드: A
  단말 노드: G,F
  크기: 7
  깊이: D=2, C=1
  높이: 3
  차수: A=2, C=1, G=0

트리의 유형

이진 탐색 트리

이진 탐색을 할 때 사용하는 자료구조
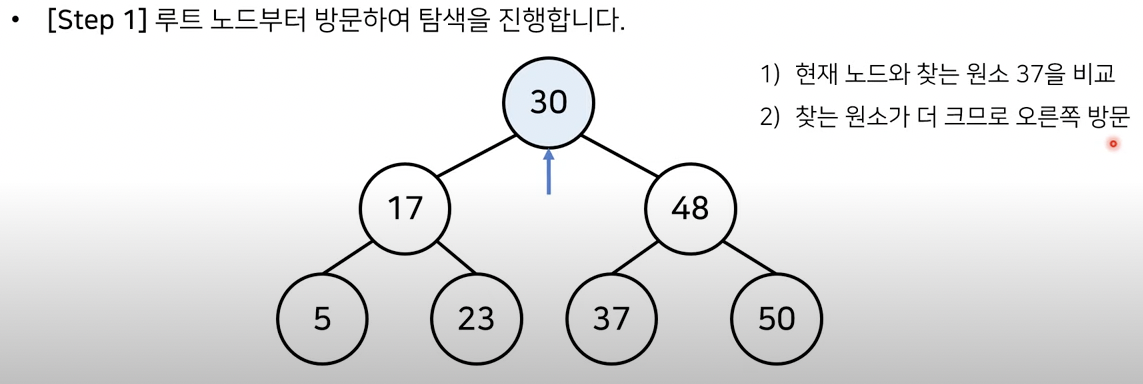
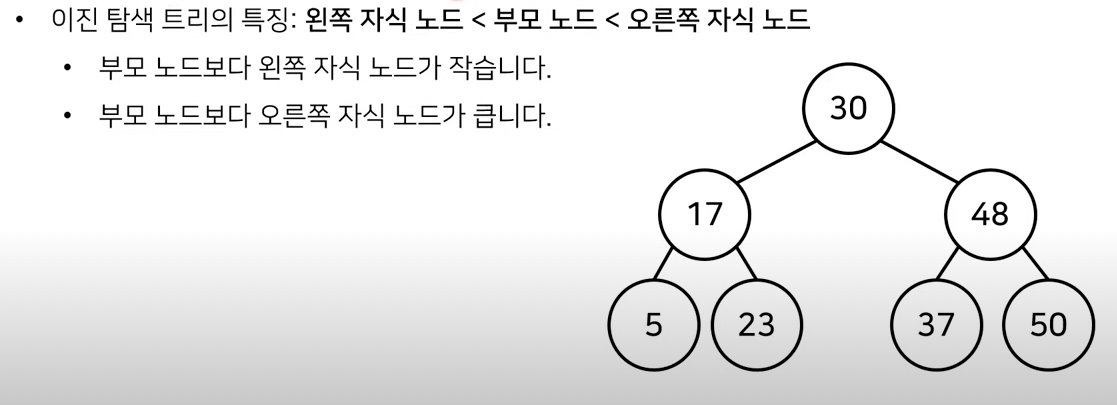예를 들어 [5,17,23,30,37,48,50]에서 37이라는 숫자의 위치를 찾으려고 합니다.
이 때 사용할 수 있는 방법은

1부터 1씩 더해보면서 37이라는 위치를 구한다.

list = [5,17,23,30,37,48,50]
for idx, number in enumerate(list):
    if number == 37:
        print(idx+1)
> 5

시간 복잡도 : O(N)

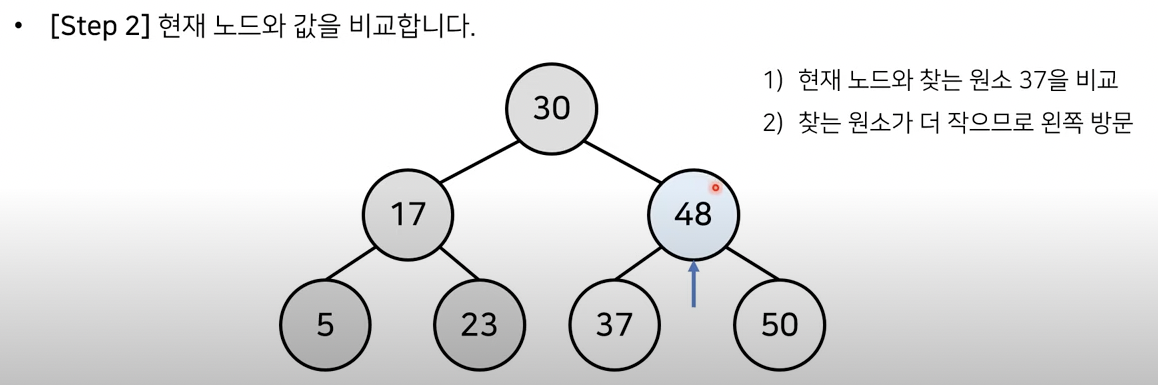
만약 위처럼 이진 탐색 트리로 구현되었다고 가정했을 땐
시간 복잡도: O(logN)

트리의 순회

트리 자료구조에 포함된 노드들을 순회하는 방법
1. 전위 순회
2. 중위 순회
3. 후위 순회

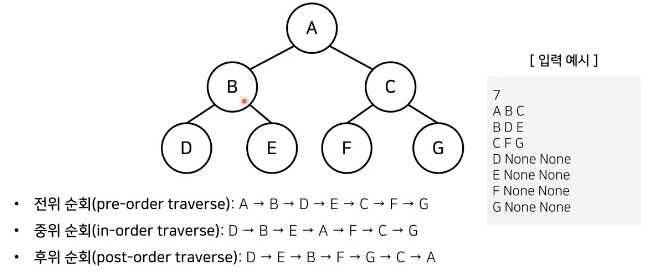
전위 순회(Pre-order)

• 루트 -> 오른쪽 자식 -> 왼쪽 자식
• 그래프의 DFS와 순서가 같다.

중위 순회(In-order)

• 왼쪽 자식 -> 루트 -> 오른쪽 자식
• 2진 트리에서 delete를 구현할 때 인오더를 주로 사용

후위 순회(Post-order)

• 왼쪽 자식 -> 오른쪽 자식 -> 루트
• 트리 관련 다이나믹 문제에서 자식이 모두 처리된 다음에 부모노드를 처리하는 방식으로 자주 쓰인다.

참고자료
개발왕, 도던
동빈나 youtube