분할정복 알고리즘

step 1 Divide - instance를 작게 쪼갬
step 2 Conquer - 재귀를 이용하여 분할한 instance들을 해결
step 3 Combine - (if necessary) 해결된 small instance 들을 다시 original instance로 병합

📌1. solve Binary Search by divide and conquer

pseudo code

public static index location(index low, index high)
{
	index mid;
    if(low>high) return 0; // index low 의 배열값이 high의 배열값 보다 크면 종료
    else{
    	mid = ⌊(low+high)/2⌋ ;
        if ( x==S[mid]) // <-basic operation 
        	return mid;
    else if (x < S[mid])
    	return location(low, mid-1) // mid 버리고 mid -1 이 high가 됨
    else 
    	return location(mid+1, high)// mid 버리고 mid +1 이 low가 됨 
        
        }
 }

👉 위 코드는 initial array (1,n)의 mid(low+high floor)를 잡고 mid 인덱스의 값을 target 값(x) 와 비교하며 (x>mid면 right side취함 x<mid면 left side 취함 ) x==mid 가 될 때 까지 반복하는 코드라고 할 수 있습니다.

시간 복잡도 분석

앞서 공부했듯이 시간복잡도 분석은 크게 2가지로 나뉩니다.

1. every-case time complexity- 모든 사이즈의 input에 대하여 basic operation의 반복횟수가 같습니다.

2. non-every case time complexity- Best Worst Average case로 나뉘며
Best case는 최소 반복횟수를 가지는 복잡도
Worst case는 최다 반복횟수를 가지는 복잡도
Average case는 평균적인 반복횟수의 기대치를 나타낸 복잡도입니다.

이진탐색 알고리즘의 b.o와 input size를 다음과 같이 정하면

basic operation : x==S[mid]

input size n(number of items in array)

W(n)(최다 반복횟수)는 다음과 같이 유도할 수 있습니다.
k번의 시행 후에 남게되는 갯수가 1 일때 시간복잡도가 worst 이므로
이를 식으로 나타내면

(1/2)^k * n ≈ 1

양변*2^k -> n ≈ 2^k
=> k ≈ lgn

🚀따라서 이진탐색의 시간복잡도는 O(lgn) 임을 알 수 있습니다.

📌2. Solve Merge Sort

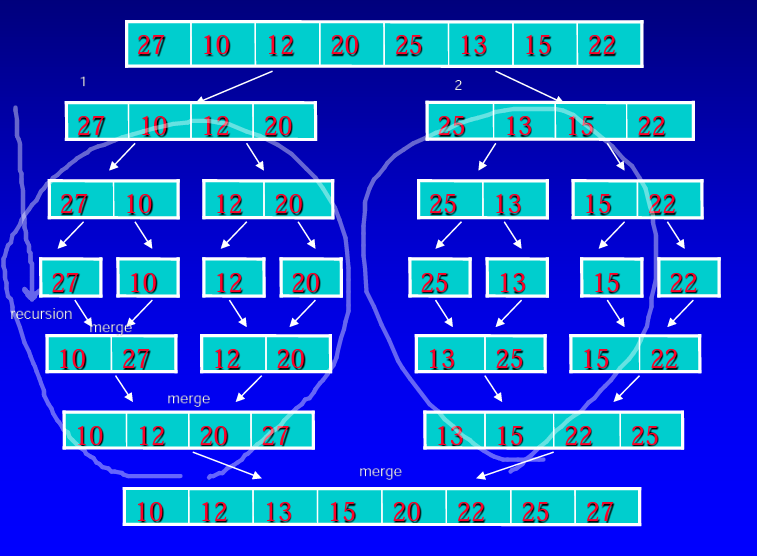
💡merge sort 란 ?
n크기의 배열을 2개의 subarray로 나눠 재귀를 이용해 각각의 배열을 정렬하고 마지막에 합치는 정렬 알고리즘 입니다.

💡💡merge sort는 step 3- combine 단계를 포함하며 combine 단계의 비교 연산이 basic operation이 됩니다.

🤔🤔🤔 왜 비교연산이 basic operation이 되나요? 대입연산까지 고려하여 시간복잡도를 산출해야하지 않나요?
👉 간단한 예시를 보겠습니다.

예시) 배열 a[2]={1,2}, b[4]={null,3,null,4} 가 있을때 b의 빈 배열에 a의 원소값을 삽입하는 연산과 오름차순으로 삽입하는 연산은 후자가 평균적으로 시간복잡도가 큽니다.

이 예시를 통해 비교연산을 b.o로 잡아야 한다는 것을 짐작할 수 있습니다.

pseudo code

public static void mergeSort(int n, keytype[] S) // n:입력크기 S:배열 길이 
{
	if(n>1) {
    	const int h = floor(n/2) , m=n-h ;
        keytype[] U = new keytype[1..h],
        		  V = new keytype[1..m] ;
        
        copy S[1:h] to U[1:h] ;
        copy S[h+1:n] to V[1:m]; // divide
        mergeSort(h,U);
        mergeSort(m,V); // 재귀함수 ->