
브루트 포스 : 비트마스크
비트연산
비트연산을 사용해서 부분 집합을 표현하는 방법
비트연산의 종류

비트연산 방법
두 수 A와 B를 비트 연산 하는 경우에는 가장 뒤의 자리부터 하나씩 연산을 수행하면 된다.

비트연산의 시간복잡도
O(1) 내부에서 알아서 상수시간 안에 처리
-
not 연산의 경우에는 자료형에 따라 결과가 달라진다.

not 연산을 할때는 내부에서 어떻게 될지를 미리 생각하자
내부에 저장되는 값은 같은데 unsigned와 signed에 따라서 보여지는 값이 다르다.(C++에 해당) 하지만 이 경우에 대해 고려할 경우가 많지는 않음 -
shift left(<<), shift right(>>)
쉬프트 연산은 shift left의 경우 0이 추가로 생기고

shift right는 가장 낮은 자리 비트를 없애버린다.
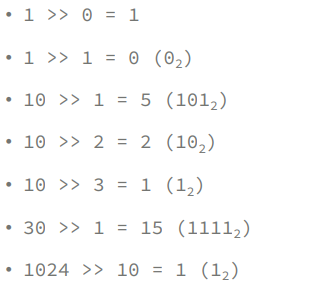
2^n을 구하려면 (1<<N)을 하면 바로 구할 수 있다.
(A+B)/2는 (A+B)>>1 로 쓸 수 있다. -
비트연산에서 중요한 것은 연산자 우선순위이다.
비트마스크 연산자 우선순위는 다른 연산자들보다 훨씬 낮다.

-
정수로 집합을 나타낼 수 있다.
비트연산의 장점은 {1,3,4,5,9}=570=2+8+16+32+512 와 같이 원래는 배열을 이용했던 것을 정수 하나로 표현할 수 있다는 장점이 있다.
- 비트마스크는 정수이다.
정수라는 점이 중요한 점이다. 정수이기 때문에 하나만 넘기어 주면 시간과 공간을 많이 절약할 수 있다.

시간도 절약되고 공간도 절약된다.

비트마스크를 사용할때는 사용하려는 수가 최대 몇개까지 있는지 반드시 알아야 한다. 왜냐하면 우리가 사용하는 int는 32bit 정수라서 2^32를 넘는 정수는 추가할 수 없다.
필수
보통 N개로 이루어져 있으면 0 ~ (N-1)까지 정수로 이루어진 집합을 나타낼 때 사용 (1~N이면 공간이 2배 더 필요)
각종 연산을 조금 변형해서 사용
여러가지 연산
-
검사
어떤 수가 포함되어 있는지 없는지 검사할때 그때는 &연산을 사용하자. 그래서 하나의 숫자를 검사할때는 비츠를 옮겨서 &연산을 통해 확인하게 된다.

-
추가
추가연산의 경우는 그 비트를 1로 바꾸어주면 된다. 바로 OR 연산을 통해 특정 위치에 값을 추가시키면 된다.

-
제거
어떤 수를 제거할때는 제거하고 싶은 비트만 0으로 만든 다음에 & 연산을 수행하면 된다.

-
토글
토글 연산도 존재하는데 0과 1을 왔다갔다 할때 주로 사용한다.

-
전체 집합
(1 << N) - 1 -
공집합
0 -
정리

정리하면 위와 같이 연산들이 존재하는 것을 예측할 수 있다.
목적
비트마스크를 사용하는 경우는 문제에서 할 수 있는게 n개 이고 그때 일부를 선택할 수 있을때 모든 방법을 만드는 경우에 사용한다.
문제
1182 부분수열의 합
N개의 정수로 이루어진 수열이 있을 때, 이 집합의 부분집합 중에서 수열의 원소를 다 더한 값이 S가 되는 경우의 수를 구하는 문제이다.
이 문제는 크기가 2^20-1 이기 때문에 재귀로 한 번 그리고 비트마스크로 한 번 풀어 볼 계획이다.
- 전체 집합 = (1<<N) - 1
- 공집합은 제외
// 1부터(공집합 제외) n-1 까지
// i는 선택된 수들의 비트를 가지고 있다. 즉, 모든 부분수열을 만들었다.
for(int i = 1; i < (i << n); i++){
// 부분 수열에 어떤 수가 들어가 있는지 확인
for(int k = 0; k < n ; ++k){
if (i&(1<<k)){
sum += a[k];
}
}
}
```python
import sys,heapq
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
n,s=map(int,input().split())
a=list(map(int,input().split()))
ans=0
def go(i,sum,n,s):
global ans
if(i>=n): return
sum+=a[i]
if(sum==s):
ans+=1
go(i+1,sum-a[i],n,s)
go(i+1,sum,n,s)
go(0,0,n,s)
print(ans)#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <algorithm>
#include <string>
#include <cstring>
#include <cstdio>
#include <functional>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <queue>
#include <map>
#define ll long long
#define len 1001
using namespace std;
int ans, i, j, m, s, w, h, nx, ny, k;
ll n;
int main(void) {
freopen("input.txt", "r", stdin);
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int n, s;
cin >> n >> s;
vector<int> a(n);
for (int i = 0; i < n; ++i) {
cin >> a[i];
}
int sum = 0, count = 0;
for (int i = 1; i < (1 << n); ++i) {
sum = 0;
for (int j = 0; j < n; ++j) {
if (i & (1 << j)) {
sum += a[j];
}
}
if (sum == s)
count++;
}
cout << count << '\n';
}14889 스타트와 링크
N명을 N/2명씩 두 팀으로 나누려고 할때 두 팀의 능력치 차이의 최솟값을 구하는 문제이다.
14391 종이 조각
N x M 크기의 종이를 조각으로 잘라서 합의 최대값을 구하는 문제(1<=N, M<=4)
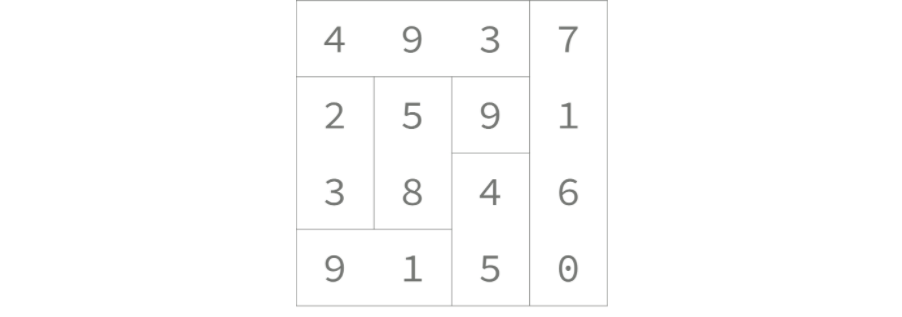
N,M제한이 4보다 작다는 것을 생각하고 문제를 풀어야 한다.
각각의 칸은 가로 또는 세로 칸에 속하게 된다.
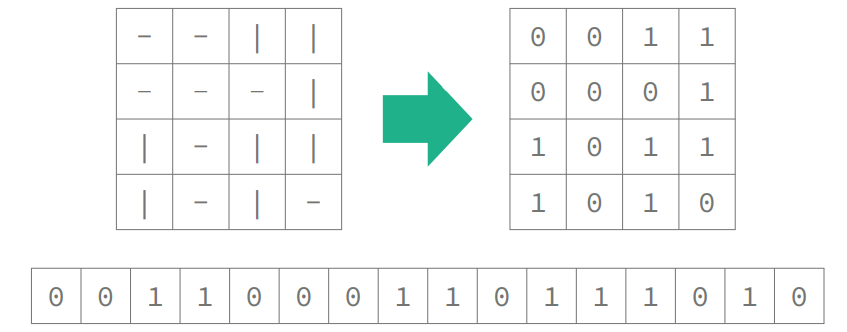
그래서 각 칸을 가로 또는 세로로 갈지를 결정해 주면 문제를 풀 수 있다.
실재로 16칸이기 때문에 2^16 = 65536 가지의 경우의 수가 존재해서 시간안에 문제를 풀 수 있다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <algorithm>
#include <string>
#include <cstring>
#include <cstdio>
#include <functional>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <queue>
#include <map>
#define ll long long
#define len 1001
using namespace std;
int ans, i, j, m, s, w, h, nx, ny, k;
ll n;
int a[4][4];
int main(void) {
freopen("input.txt", "r", stdin);
ios_base::sync_with_stdio(false);
//cin.tie(nullptr);
//cout.tie(nullptr);
int n, m;
cin >> n >> m;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
scanf("%1d", &a[i][j]);
}
}
int ans = 0;
// 0 : 가로, 1 : 세로
for (int s = 0; s < (1 << (n * m)); ++s) {
int sum = 0;
//가로
for (int i = 0; i < n; ++i) {
int cur = 0;
for (int j = 0; j < m; ++j) {
int k = i * m + j;
if ((s & (1 << k)) == 0) {
cur = cur * 10 + a[i][j];
}
else {
sum += cur;
cur = 0;
}
}
sum += cur;
}
//세로
for (int i = 0; i < m; ++i) {
int cur = 0;
for (int j = 0; j < n; ++j) {
int k = j * m + i;
if ((s & (1 << k))!=0) {
cur = cur * 10 + a[j][i];
}
else {
sum += cur;
cur = 0;
}
}
sum += cur;
}
ans = max(ans, sum);
}
cout << ans << '\n';
}14225 부분수열의 합
수열 S가 주어졌을 때, 수열S의 부분수열의 합으로 나올 수 없는 가장 작은 자연수를 구하는 문제이다. 앞에서 보았던 문제와는 약간의 반대 개념으로 생각할 수 있다.
시간 복잡도는
2^N(나오는 경우의 수) * N(계산 시간)
N <= 20 이기 때문에 제한 시간안에 문제를 푸는 것이 가능하다.
그래서 내가 볼때는 그냥 뺑뺑이 돌리면서 나온 결과값을 체크를 하는 배열에 저장하고 1부터 시작해서 배열에 값이 0인 가장 작은 값을 찾으면 될듯 하다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <algorithm>
#include <string>
#include <cstring>
#include <cstdio>
#include <functional>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <queue>
#include <map>
#define ll long long
#define len 1001
using namespace std;
int ans, i, j, m, s, w, h, nx, ny, k;
ll n;
bool check[20 * 100000 + 10];
int a[20];
int main(void) {
freopen("input.txt", "r", stdin);
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int t;
cin >> t;
for (int i = 0; i < t; ++i) {
cin >> a[i];
}
int sum = 0;
for (int i = 1; i < (1 << t); ++i) {
sum = 0;
for (int j = 0; j < t; ++j) {
if (i & (1 << j)) {
sum += a[j];
}
}
check[sum] = true;
}
for (int i = 1;; ++i) {
if (check[i] == false) {
cout << i << '\n';
break;
}
}
}내가 마지막에 실수한 부분이 있는데 for 문 마지막에 검사하는 부분은 반드시 조건이 없어야 한다. 왜냐하면 어디까지 수가 없을지 알 수 가 없지만 어찌되었든 반드시 없는 수가 나올 수 밖에 없는 구조이기 때문이다.
1062 가르침
N개의 단어가 주여졌을 때 K개의 글자로만 이루어진 단어의 개수를 고르는 문제. 하지만 모든 단어는 anta로 시작하고 tica로 끝나야 한다. 그러면 antic는 항상 포함이 되어야 한다. 그렇다면 2^21개에서 k-5개의 글자를 고르는 시간이 시간복잡도가 된다.
각각의 단어에 대해서 모든 글자를 검사해야 한다. (N x 15)
따라서 시간복잡도는 2^21 x 50 x 15 = 157,286,400의 시간이 걸리게 된다.
그래서 이것의 시간을 줄이기 위해 비트마스크를 사용하자. 각 단어가 구성하고 있는 알파벳이 무엇인지 알아야 한다.
