탐욕법 greedy algorithm
그리디 알고리즘은 가급적 CPP로 풀자
겨울 알고리즘
그냥 순진하게 모든 경우를 하면 시간, 공간 복잡도 측면에서 비효율적
모든 선택지를 고려하지 않고, 각 단계마다 지금 가장 좋은 방법만을 선택 -> 즉 사용자가 처음부터 어떤 케이스만을 고려하게 된다.
이때 정당성 증명이 굉장히 중요하다.
그리디 알고리즘이 항상 성립할까? 우리가 선택한 방법의 경우로만 탐색하기 때문에 최적해가(실제 정답) 나오지 않을 수도 있다.
그래서 그리디 알고리즘의 정당성을 증명하는 것이 중요하다. 증명하는 방법은 다음 두가지 방법이 사용된다.
1. 탐욕적으로 선택하더라도 문제의 최적해를 구할 수 있다.
2. 부분 문제의 최적해에서 전체 문제의 최적해를 만들 수 있다.
탐욕적 선택 속성 : 각 단계에서 탐욕적으로 내리는 선택은 항상 최적해로 가는 길 중 하나
최적 부분 구조(중요) : 부분 문제의 최적해에서 전체 문제의 최적해를 만들 수 있다. 대부분 자명한 경우가 많다.
문제는 어떤 방법을 선택하고 그것의 정당성을 증명하는 과정이 어렵다.
문제
1931 회의실 배정
결국에는 끝나는 시간이 중요한 문제이다. 그렇기 때문에 끝나는 시간을 우선 정렬하고 회의가 끝나자마자 다음 회의를 시작하면 된다.
회의실 배정문제가 최적해 보장 문제인지를 증명
1. 어떤 회의 선택시 시간이 겹치는 회의는 선택 불가능
2. 남은 회의들 집합에 대해서도 최대한 많은 회의가 진행되어야 한다.
따라서 최적 부분 문제이다.
방법을 생각해보자
1. 시작 시간은 기준이 될 수 없다.
2. 짧은 회의를 그리디하게 풀 수도 없다.
3. 끝나는 시간으로 그리디하게 풀 수 있다.
증명을 위해 귀류법을 이용
우리 선택이 최적화로 가지 못하고 최적화가 P라는 경우뿐일때 최적해가 존재하는 선택은 그리디하지 못하다.
귀류법이 결론에 모순이 있다 가정하고 가정의 모순이 있는 것을 증명해서 결론이 참임것을 증명하는 방법이다.
여기에서는 끝나는 시간으로 그리디하게 풀면 최적해를 구할 수 있다는 것이다. 만약에 끝나는 시간으로 그리디하게 풀 수 없다고 하면 빨리시작하는 회의 혹은 짧은 회의를 선택해야 하는데 이러한 풀이로는 최적회를 구할 수 없다.
//입출력 속도 향상
//c문법과 동기화를 멈추겠다.
ios_base::sync_with_stdio(0);
cin.tie(0), cout.tie(0);암튼 풀이
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <string>
#define ll long long
#define len 1001
using namespace std;
int main(void) {
freopen("input.txt", "r", stdin);
ios_base::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int t = 0;
vector<pair<int, int>> a(t);
cin >> t;
for (int i = 0; i < t; ++i) {
cin >> a[i].second >> a[i].first;
}
sort(a.begin(), a.end());
int ans = 1;
pair<int, int> pos = a[0];
for (int i = 1; i < t; ++i) {
if (pos.first < a[i].second) {
ans += 1;
pos = a[i];
}
}
cout << ans;
}14659 한조서열정리하고옴ㅋㅋ
계속해서 큰 놈만 업데이트 해주고 값을 구해주면 되는 문제이다.
여기에서 중요한 것 중 하나가 PS분야 문제 풀이는 전역변수를 많이 사용한다. 보통 전역변수는 초기화 해주지 않아도 0으로 초기화 되어있다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <string>
#define ll long long
#define len 1001
using namespace std;
int ans, big,i;
int main(void) {
freopen("input.txt", "r", stdin);
ios_base::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int t = 0;
cin >> t;
vector<int> a(t);
for (i = 0; i < t; ++i) {
cin >> a[i];
}
for (i = 0; i<t; ++i) {
if (a[big] <= a[i]) {
ans = max(ans,i - big-1);
big = i;
}
}
ans = max(ans, i - big - 1);
cout << ans;
}20044 Project Teams
문제는 두 명이 한 팀이 될때 일정한 밸런스를 맞추게 하고 최대가 되는 최솟값을 찾아내는 문제이다.
그냥 정렬하고 맨 뒤와 앞을 합쳐주면 최적해가 나온다.
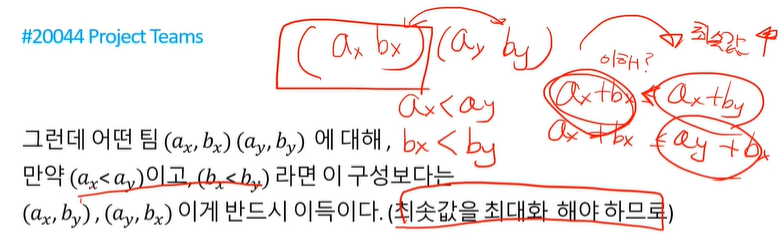
ax<ay 이고 bx<by 이면 ax+bx<ax+by 인 것이 당연하다. 우리는 최솟값이 최대가 되어야 하기 때문에 섞는 것이 오히려 최대인 최솟값을 보장한다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <string>
#define ll long long
#define len 1001
using namespace std;
int ans, big,i;
int main(void) {
freopen("input.txt", "r", stdin);
ios_base::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int t = 0;
cin >> t;
t *= 2;
vector<int> a(t);
for (int i = 0; i < t; ++i) {
cin >> a[i];
}
sort(a.begin(), a.end());
ans = -1;
for (int i = 0; i < t; ++i) {
if (ans == -1 || a[t - 1 - i] + a[i] < ans) {
ans = a[t - 1 - i] + a[i];
}
}
cout << ans;
}2847 게임을 만든 동준이
그냥 끝에서부터 자기랑 비슷하거나 큰 것을 자기의 점수보다 1점 적게까지 깎아주면 된다.
이게 그리디인지는 모르겠으나 제한이 100이라서 O(n^2)의 알고리즘으로도 풀린다.
어떤점에서 한조서열정리하고옴과 비슷한 문제라고 보인다.
import sys
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
t=int(input())
a=list(int(input()) for _ in range(t))
c=0;
for i in range(t-1,-1,-1):
for j in range(i-1,-1,-1):
if a[i]<=a[j]:
c+=a[j]-a[i]+1
a[j]=a[i]-1
print(c)import sys
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
t=int(input())
a=list(int(input()) for _ in range(t))
c=0;
for i in range(t-2,-1,-1):
if(a[i]>=a[i+1]):
c+=a[i]-(a[i+1]-1)
a[i]=min(a[i],a[i+1]-1)
print(c)4796 캠핑
이게 왜 그리디인지 모르겠지만 일단 그냥 연속 날짜를 기준으로 내 휴일을 나누어 버리면 된다. 문제는 내 휴일 중에서 남은 부분 처리인데 이것만 잘 처리하면 문제는 쉽게 풀린다.
import sys,heapq
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
l,p,v=map(int,input().split())
i=1
while l !=0 and p!=0 and v!=0:
ans=0
ans+= int(v/p)*l
if(v%p>=l):
ans+=l
else:
ans+=v%p
print("Case {0}: {1}".format(i,ans))
i+=1
l,p,v=map(int,input().split())2839 설탕 배달
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <string>
#define ll long long
#define len 1001
using namespace std;
int ans, i;
int main(void) {
freopen("input.txt", "r", stdin);
int n;
scanf("%d", &n);
bool flag = true;
int ans = 0;
while (n > 0) {
if (n % 5 == 0) {
ans += n / 5;
flag = false;
break;
}
else {
ans += 1;
n -= 3;
}
}
if (flag && n!=0) {
printf("-1");
}
else {
printf("%d", ans);
}
}백준
결정해야 할 때, 그 순간에 가장 좋다고 생각하는 것을 선택하면서 답을 찾아가는 알고리즘(즉, 무조건 가장 크거나 작은 것을 선택하는게 아닌 그 순간의 최적의 방법으로 문제를 푸는 것)
그때 그때는 최적일지도 모르지만, 최종적으로는 답이 최적이 아닐 수 있다. 왜냐하면 그 순간에서는 최적이지만 나중에는 최적이 아닐 수 있기 때문에 전체에 공통적으로 적용되는 최적 방법을 찾아야만 한다. 그리고 그것을 또 귀류법으로 증명해야 한다.
증명방법은 귀류법으로 사용한다. 그래서 이것은 그리디가 아니다를 가지고 반례를 찾아 그리디임이 참임을 증명하면 된다.
- 탐욕적으로 선택하더라도 문제의 최적해를 구할 수 있다.
- 부분 문제의 최적해에서 전체 문제의 최적해를 만들 수 있다.
1. 정렬
문제
11047 동전 0
규칙 : 큰 값부터 나누어도 최적해가 나온다.
import sys
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
t,m=map(int,input().split())
a=list(int(input()) for _ in range(t))
a.reverse()
ans=0
for i in range(t):
if(m/a[i]!=0):
ans+=int(m/a[i])
m%=a[i]
if(m==0): break
print(ans)1931 회의실 배정
import sys
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
t=int(input())
a=[]
for i in range(t):
temp=list(map(int,input().split()))
temp.reverse()
a.append(temp)
a.sort()
ans=1
max=a[0][0]
for i in range(t-1):
if(max<=a[i+1][1]):
ans+=1
max=a[i+1][0]
print(ans)11399 ATM
사람별로 돈을 뽑는 시간이 있고 순서에 따라 총 뽑는 시간의 차이가 생긴다.
만약 이걸 그리디하게 푼다고 하면 작은 문제에서 최소가 나오게 하는 방법밖에 없으니 그냥 오름차순으로 푸는 문제가 될 것이다.
import sys
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
t=int(input())
a=list(map(int,input().split()))
a.sort()
ans=[a[0]]
for i in range(1,t):
ans.append(a[i]+ans[i-1])
print(ans[t-1])2. 뒤집기
문제
1080 행렬
이게 어떻게 그리디 알고리즘인지 이해할 수가 없다.

일당 대충 보아서 3x3을 바꾼다고 했을때 1,1 위치가 A와 B와 다르다면 바꾸어야 한다. 이와 같이 모두 행렬을 3x3만큼 바꾸었을 때 딱 한번만 요구되는 칸들이 존재한다.
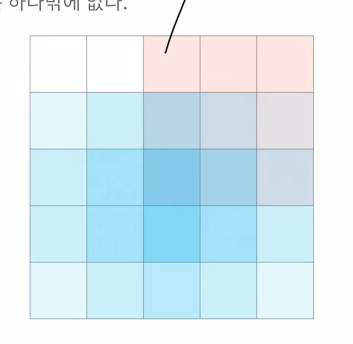
계속 이 방법을 사용하지 않을지를 3x3 칸의 1,1위치만을 검사해주는 것이다.
import sys
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
m,n=map(int,input().split())
a=[list(map(int,list(input().rstrip()))) for _ in range(m)]
b=[list(map(int,list(input().rstrip()))) for _ in range(m)]
ans=0
def flip(y,x):
for i in range(0,3):
for j in range(0,3):
a[y+i][x+j]=abs(1- int(a[y+i][x+j]))
for i in range(m-2):
for j in range(n-2):
if(a[i][j]!=b[i][j]):
flip(i,j)
ans+=1
for i in range(m):
for j in range(n):
if(a[i][j]!=b[i][j]):
print(-1)
sys.exit(0)
print(ans)
2138 전구와 스위치
첫번째 칸을 결정하면 각칸을 어떻게 할지에 대한 경우의 수 1개가 생긴다. 즉 첫번째 칸을 누르고 안누르고에 따라 두가지 경우가 생긴다. 작은문제로 생각해서 앞에 있는 칸에서 이미 맞추어 졌다면 이번에 누르는 것 역시 최적해가 나온다는 것을 예상해 볼 수 있다.
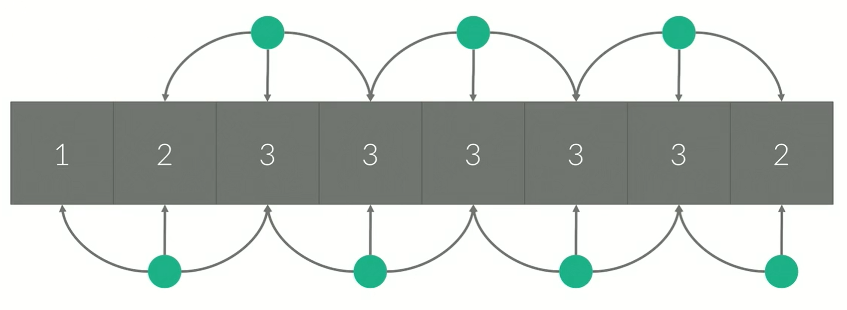
import sys
sys.stdin=open("input.txt","r")
input=sys.stdin.readline
t=int(input())
a=list(map(int,list(input().rstrip())))
b=list(map(int,list(input().rstrip())))
def swap(a,i):
if(i!=0): a[i-1]=not a[i-1]
a[i]=not a[i]
if(i!=t-1): a[i+1]=not a[i+1]
def go(a,b):
ans=0
for i in range(t-1):
if(a[i]!=b[i]):
swap(a,i+1)
ans+=1
if(a==b): return True,ans
else: return False,ans
temp=a[:]
f,fv=go(a,b)
a=temp[:]
swap(a,0)
s,sv=go(a,b)
if(s): sv+=1
if(f and s):
print(min(fv,sv))
elif(f):
print(fv)
elif(s):
print(sv)
else:
print(-1)1285 동전 뒤집기
이 문제도 위와 같이 특정 위치를 뒤집은 다음에 생각해 봐야 하는데 문제는 그렇게 하기에는 1이라는 숫자가 너무 많다. 하지만 우리가 구하고자 하는 것은 동전의 한행/열을 뒤집어서 앞면의 수를 늘리는 것이기 때문에 한 열을 쭉 따라 앞면이 많도록 만들고 그 다음 행을 따라 앞면이 많도록 하면 되지 않을까?

일단 비트마스크를 공부해야 겠다. 뭔소리인지 모르겠다...
#include <iostream>
#include <algorithm>
#include <string>
#include <vector>
using namespace std;
char flip(char x) {
if (x == 'H') return 'T';
else return 'H';
}
int main() {
int n;
cin >> n;
vector<string> a(n);
for (int i=0; i<n; i++) {
cin >> a[i];
}
int ans = n*n;
for (int state=0; state<(1<<n); state++) {
int sum = 0;
for (int j=0; j<n; j++) {
int cnt = 0;
for (int i=0; i<n; i++) {
char cur = a[i][j];
if (state & (1 << i)) {
cur = flip(cur);
}
if (cur == 'T') {
cnt += 1;
}
}
sum += min(cnt, n-cnt);
}
if (ans > sum) ans = sum;
}
cout << ans << '\n';
return 0;
}3. 기준
문제
1202 보석도둑(기준 그리디)
이 문제는 주어진 조건이 보석의 가격과 무게 그리고 가방이 넣을 수 있는 최대 무게로 보석과 가방을 기준으로 각각 문제를 다르게 풀 수 있다.
- 각각의 보석이 어떤 가방에 들어가야 하는지 조사하는 방법
가장 가치가 높은 보석부터 어떤 가방에 들어가야 할지를 조사 -> C[i]가 가장 작은 가방부터 해서 보석을 넣을 수 있는 최소 무게의 가방을 우선 선택한다.
cpp 로 푼다면 multiset을 사용한다.
multiset 은 중복된 값이 들어갈 수 있다.
multiset<int> ms;
ms.insert(9)
//시작과 끝 위치를 각각 설정해 줄 수 있다.
multiset<int>::iterator start,end;
//Key값 11이 처음 나온 부분[폐구간]
start=ms.lower_bound(11);
//key값 11이 나온 부분의 다음(개구간)
end=ms.upper_bound(11);- 각각의 가방에 들어갈 가장 좋은 보석을 조사하는 방법
가장 좋다는 것은 가격이 비싸다는 것을 이야기 한다. 보석과 가방을 하나로 합치고 무게를 기준으로 오름차순 정렬하자
후보를 이용하자 : 후보는 가방에 들어갈 수 있는 보석을 의미
보석과 가방을 하나로 합치고 무게를 기준으로 오름차순 정렬하자
(1,23),(2,99),2,(5,65),10
보석은 지나가다가 가방이 나오면 그 앞에 보석은 모두 가방에 들어갈 수 있는 보석이다.
후보는 최대값을 구해야 하니 최대힙을 이용해서 구해야 한다. 우선순위 큐를 활용하자.
(N+K)logN
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <string>
#include <queue>
#define ll long long
#define len 1001
using namespace std;
struct jewel {
int m, v, w;
};
int ans, i;
int main(void) {
freopen("input.txt", "r", stdin);
int n, k;
scanf("%d %d", &n, &k);
vector<jewel> a(n+k);
for (int i = 0; i < n; ++i) {
scanf("%d %d", &a[i].m, &a[i].v);
}
for (int i = 0; i < k; ++i) {
scanf("%d", &a[i + n].m);
a[i + n].w = 1;
}
sort(a.begin(), a.end(), [](jewel u, jewel v) {
return u.m < v.m || (u.m == v.m && u.w < v.w);
});
priority_queue<int> q;
long long ans = 0;
for (auto &it : a) {
if (it.w == 0) {
q.push(it.v);
}
else {
if (!q.empty()) {
ans += q.top();
q.pop();
}
}
}
printf("%lld", ans);
}2109 순회강연(기준 그리디)
N개의 대학에서 강연 요청을 했다. 강연 요청은 두 개의(d,p)이고 d일 안에 와서 강연을 하면 p원의 강연료를 준다.
하루에 최대 한 곳에서만 강연을 할 수 있다고 가정했을 때 최대 수익을 구하는 문제.
강연 = (20,1),(2,1),(10,3),(100,2),(25,2) 로 나열되어 있을 때 최댓값은 3이기 때문에 4일부터는 강연이 불가능하다.
이 문제는 강연 날짜보다 현재 날짜가 작거나 같으면 강연이 가능한 문제이다.
그래서 보석도둑과 동일하게 (가격,날),기간으로 저장하자. 그리고 d를 기준으로 내림차순 정렬을 했다. 보석도둑에서는 분명 가방의 문게를 기준으로 오름차순 정렬을 한것과는 대조적이다.
구현 방식도 굉장히 이질적이다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <string>
#include <queue>
#define ll long long
#define len 1001
using namespace std;
struct pay {
int p, d;
};
int ans, i;
int main(void) {
freopen("input.txt", "r", stdin);
int n;
scanf("%d", & n);
vector<pay> a(n);
for (i = 0; i < n; ++i) {
scanf("%d %d\n", &a[i].p, &a[i].d);
}
sort(a.begin(), a.end(), [](pay u, pay v) {
return u.d > v.d;
});
int k = 0;
priority_queue<int> q;
ll ans = 0;
for (i = 10000; i >= 1; --i) {
/* 즉 여기에서는 우리가 선택할 수 있는 것들만을 다 넣어준다. */
while (k < n && a[k].d == i) {
q.push(a[k].p);
k++;
}
if (!q.empty()) {
ans += q.top();
q.pop();
}
}
printf("%lld", ans);
}4. lower_bound, upper_bound
문제
12015 가장 긴 증가하는 부분 수열2
기준이 매우 크기 때문에 dp를 사용할 수 없고 그리디를 만들어야 한다.
그냥 증가하는 부분수열을 다 만들어 본다.
{1,3,1,2,4,3,4,2}로 존재한다고 할때
1, 3/1,3 ... 으로 계속 생길 것이다. 하지만 여기에서 3 단독은 필요없다. 이미 1이 있어 길이가 늘어나지 않기 때문이다.
하지만 이렇게 하면 너무 오래걸린다. O(n^2)의 시간이 필요하니까 말이다.
1
1,2
1,2,3
1,2,3,4
와 같이 가장 긴것만 알면 되기 때문에 92이렇게 하지 말고 나온 값을 기준으로 계속 dp에 넣어준다. 그리고 가장 큰 값보다 작은 값이 나오면 바꾸고 큰 값이 나오면 추가해준다.

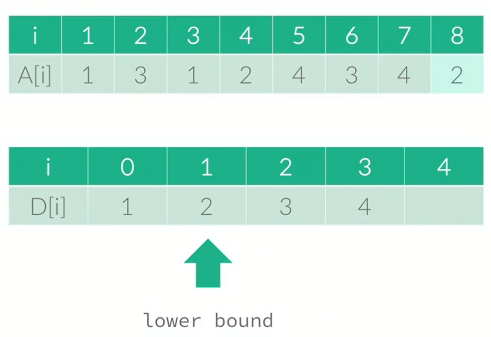
이 방식을 이용하면 가장 긴 것의 길이만을 구할 수 있다. NlogN만에 구할 수 있다. 이분탐색을 사용해야 한다.
이분탐색을 써야 하는 만큼 lower_bound의 사용이 필수적이라서 cpp로 문제를 풀었다.
value 값보다 큰 값중에 가장 작은 값을 찾아낸다.
lower_bound( begin(), end(), value);#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <string>
#include <queue>
#define ll long long
#define len 1001
using namespace std;
int ans, i;
int main(void) {
freopen("input.txt", "r", stdin);
int n;
scanf("%d", & n);
vector<int> a;
for(i=0;i<n;++i){
int temp;
scanf("%d ", &temp);
auto it = lower_bound(a.begin(), a.end(), temp);
if (it == a.end()) {
a.push_back(temp);
}
else {
*it = temp;
}
}
printf("%d", a.size());
}12738 가장 긴 증가하는 부분 수열 3
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <string>
#include <queue>
#define ll long long
#define len 1001
using namespace std;
int ans, i;
int main(void) {
freopen("input.txt", "r", stdin);
int n;
scanf("%d", & n);
vector<int> a;
for(i=0;i<n;++i){
int temp;
scanf("%d ", &temp);
auto it = lower_bound(a.begin(), a.end(), temp);
if (it == a.end()) {
a.push_back(temp);
}
else {
*it = temp;
}
}
printf("%d", a.size());
}5. 분류
문제
1541 잃어버린 괄호
식에 괄호를 적절히 쳐서 식의 값을 최소로 만드는 문제
가장 큰 값을 빼주는 문제이기 때문에 -가 나왔다면 바로 뒷편의 +를 모두 묶어주는 방식으로 문제를 풀 수 있다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <string>
#include <queue>
#define ll long long
#define len 1001
using namespace std;
int ans, i;
int main(void) {
freopen("input.txt", "r", stdin);
string str;
cin >> str;
vector<int> sign;
vector<int> val;
sign.push_back(1);
int num = 0;
for (int i = 0; i < str.size(); ++i) {
if (str[i] == '+' || str[i] == '-') {
sign.push_back(str[i] == '+' ? 1 : -1);
val.push_back(num);
num = 0;
}
else {
num = num * 10 + (str[i] - '0');
}
}
val.push_back(num);
ll ans = 0;
bool minus = false;
for (i = 0; i < val.size(); ++i) {
if (sign[i] == -1) {
minus = true;
}
if (minus) {
ans -= val[i];
}
else {
ans += val[i];
}
}
printf("%lld", ans);
}1744 수 묶기
길이가 N인 수열에서 두 수를 적절히 묶고 곱해서 수열의 합을 최대로 하는 문제
- 양수는 큰 수끼리 묶고
- 음수는 작은 수 끼리 묶는다
- 묶이지 않은 음수는 0을 이용할 수 있다.
- 1은 묶지 않는 것이 최대
그래서 음수는 오름차순
양수는 내림차순해주고
양수의 수가 홀수면 1을 추가로 넣어주고
음수의 수가 홀수면 0을 있는 갯수만큼만 넣어준다.
이 방식으로 모든 수가 한번은 묶일 수 있게 만든다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#include <cmath>
#include <stack>
#include <string>
#include <queue>
#define ll long long
#define len 1001
using namespace std;
int ans, i,n;
int main(void) {
freopen("input.txt", "r", stdin);
ios_base::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t;
cin >> t;
vector<int> plus;
vector<int> minus;
int zero = 0;
int one = 0;
for (i = 0; i < t; ++i) {
int d;
cin >> d;
if (d == 0) {
zero++;
}else if(d>1) {
plus.push_back(d);
}
else if(d<0){
minus.push_back(d);
}
else {
one++;
}
}
if (plus.size() % 2 == 1) plus.push_back(1);
if (minus.size() % 2 == 1) minus.push_back(zero > 0 ? 0 : 1);
sort(plus.begin(), plus.end(), greater<>());
sort(minus.begin(), minus.end());
ll ans = one;
for (i = 0; i < plus.size(); i += 2) {
ans += plus[i] * plus[i + 1];
}
for (i = 0; i < minus.size(); i += 2) {
ans += minus[i] * minus[i + 1];
}
cout << ans << '\n';
}