기초 인공지능 16

무인 자동차 예시를 통해서 시작한 강의

만약 문제가 생기었을 때 머신러닝을 비롯한 인공지능은 매 상황에 대해 자신은 이성적인 판단을 하였지만 결과적으로 이성적이지 않은 결론 일 수도 있기에 인공지능만으로 모든 일을 처리한다는 것은 쉬운 일이 아니다.

사람과 같은 경우 사람과의 관계를 통해서 경험이 축적된다. 그렇지 않다면 사람에 대한 정보를 얻을 수 있는 것이 거의 없다.

또한 기존의 지식과 정보는 이후의 지식과 정보를 다루고 처리하는데 전혀 도움이 되지 않는다. 그래서 추론을 한다는 것이 어렵다.

우리가 이 다원에서 다루는 것 : propositionalization(명제 논리화)

9.3 Forward Chaining

p라는 조건과 q라는 조건이 만족하면 그 안에 있는 변수가 unify로 통합되면 결론을 도출하고 결론은 다시금 substitution(변환)해서 지속적으로 결론을 도출해 나가는 것을 Forward Chaining이라고 부른다.

Generalized Modus Ponens(9.2.1)을 찾아서 계속해서 진행한다. 이때 Generalized Modus Ponens는 어느 정도 합당한 clause를 이야기 한다.

9.3.1 First-order definite clauses

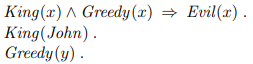
이제 First-order logic이 적용된 사례를 보도록 하자 위와 같이 King 이면서 Greedy 하다면 Evil 하다는 결론은 Reasoning 할 수 있다.

이때 First-order logic을 programming 하기 위한 언어가 존재한다.

9.4.2 Logic programming
logic programming language 중 가장 많이 사용하는 것이 Prolog로 Prolog는 First order logic을 그대로 표현한 것이다.

적어도 AI는 First-order logic을 이용하여서 알고리즘 처럼 사용할 수는 있겠으나 아직까지는 생으로 프로그래밍하는 것은 가능하지 않다.

9.3.2 A simple forward-chaining algorithm(시험)

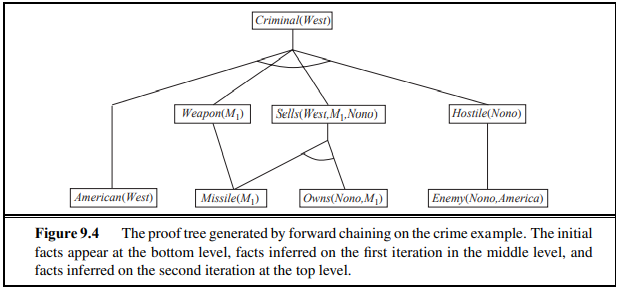
이게 위와 같이 forward chaining을 만들어 내는 것을 proof tree라고 부른다.

이는 추후에 나올 backward-chaining과 비슷하다.
backward-chaining은 차사고가 났을 때 환자나 자동차에 모든 정보가 저장되어 있을 때, 진단하는 것이 더 중요한 것과 같이. 사고가 난 과정을 찾아내는 것을 backward-chaining이라고 부른다.

그래서 처음에는 forward chaining을 통하여서 결론에 이르기 까지 진행을 하고 이후에 결론이 완벽하지 못하면 가정을 세우고 그 과정에 맞는 데이터인지 확인하기 위한 backward-chaining의 과정을 진행한다.

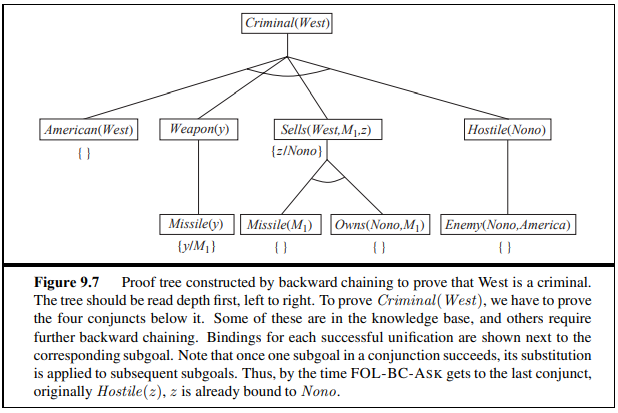
9.4.1 에서 나오는 backward-chaining의 proof tree는 forward chaining과 다르게 역으로 추론해 나가는 방식으로 진행한다는 것을 이 트리를 통하여서 확인해 볼 수 있다.

그렇기에 실재 과정에서는 forward와 backward를 함께 수행하여서 원하는 결론을 도출하여 낸다.

---

Incremental forward chaining

다양한 성능 상승 방법이 나왔음에도 불구하고 Reet network는 production system=rule based system의 가장 중요한 성분이다. 이는 첫번째 forward-chaining system 이였다.

그리고 이후에는 general-purpose를 위해 제작된 Ops-5 와 같은 언어도 제작되기도 하였다.

9.5 Resolution

9.5.1 Conjunctive normal form for first-order logic

first-order resolution은 CNF가 필요하다.

위의 예제는 일반 식을 CNF로 바꾸는 것을 확인해 볼 수 있다.

그래서 CNF로 바꾸는 과정은 아래의 단계를 따르게 된다.

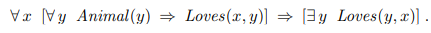
위와 같은 식이 존재한다고 할때

• Eliminate implications
  
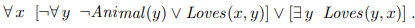
  Eliminate implications에 따라 ⇒을 제거한다.

• Move ¬ inwards
  
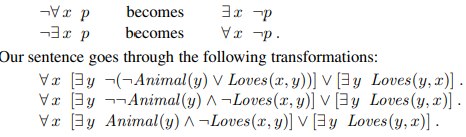
  ¬로 표시도니 부분을 모두 바꾼다.

• Standardize variables
  
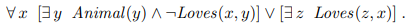
  (∃x P(x))∨(∃x Q(x))
  

• Skolemize
  ∀y ∃x Q(x,y) 에 대해서 x만이 영향이 있기에 실질적으로 x=F(y)라고 생각해보면(이때 x=F(y)를 Skolemize라고 부른다.) Q(F(y),y)이다.

• Drop universal quantifiers
  

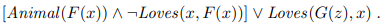
• Distribute ∨ over ∧:
  

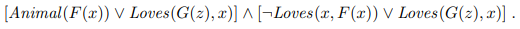
9.5.4 Completeness of resolution
Robinson이라는 사람이 resolution rule은 활용할 수 있다고 증명하기도 하였다.

이때의 resolution rule 중에 하나인 (A + B) * (C + ~B) = (A + C) 가 된다는 것과 같은