1. 이동문제 : DP 점프점프 유형
시간복잡도
O(n^2) => 하지만 이건 풀이법을 달리하면 O(n)으로 바뀐다.
알고리즘
다이나믹 프로그래밍 일명 DP를 풀때는
1. 점화식이 있는 유형인 경우
- 점화식이 있다면 우선적으로 점화식을 세운다
- 배열이 무엇을 의미하는지 정의한다.
- 초기화 한다.
의 세 단계로 왠만큼 문제가 풀린다.
키워드
문제가 점점 작아진다.
점화식이 있다.
점프점프 유형은 문제에 이동가능한 거리가 주어진다.
최대 최소값을 구하는 것이 문제의 주요포인트이다.
문제
11048 이동하기
문제에서 방향을 고정해 두었다. 오른쪽, 오른쪽 대각선, 아래쪽
그렇기 때문에 문제는 진행될 수록 점점 작아지는 구조를 가지게 된다.
1) 방법 1 : 점화식
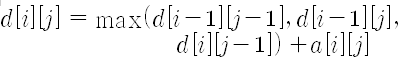
점화식을 세워서 쉽게 풀 수 있다.
대신 언제나 이야기 하듯 알고리즘 문제를 풀때는 STL은 쓸 수 있으면 쓰는게 좋다.
여기에서도 max함수에 임시 리스트를 넣고 돌리어서 풀었다.
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
#include <queue>
#include <cstdlib>
#include <cstring>
#define ll long long
#define len 1001
using namespace std;
int a[len][len];
int d[len][len] = { 0 };
int main(void) {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
freopen("input.txt", "r", stdin);
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
cin >> a[i][j];
}
}
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
d[i][j] = max({ d[i - 1][j - 1],
d[i - 1][j], d[i][j - 1] }) + a[i][j];
}
}
cout << d[n][m];
}2) 방법 2
3) 방법 3
4) 방법 4
5) 방법 5
11060 점프 점프
가장 마지막 위치는 분명 그 전 어떤 위치에서 왔을 것이기 때문에 간단히 점화식을 세우면 아래와 같이 만들 수 있다.
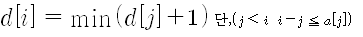
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
#include <queue>
#include <cstdlib>
#include <cstring>
#define ll long long
#define len 1001
using namespace std;
int a[len];
int d[len];
int main(void) {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
freopen("input.txt", "r", stdin);
int n;
cin >> n;
for (int i = 0; i < n; ++i) {
cin >> a[i];
}
memset(d, -1, sizeof(d));
d[0] = 0;
for (int i = 1; i < n; ++i) {
for (int j = 0; j < i; ++j) {
if (d[j] != -1 && i - j <= a[j]) {
if ((d[j] + 1) < d[i] || d[i] == -1) {
d[i] = d[j] + 1;
}
}
}
}
cout << d[n-1] << '\n';
}하지만 이 방식으로는 O(n^2) 밖에 풀 수 없기 때문에 매우 안좋다.
이를 개선한 것이 현재를 시점으로 갈 수 있느 곳을 체크하는 방법이다.
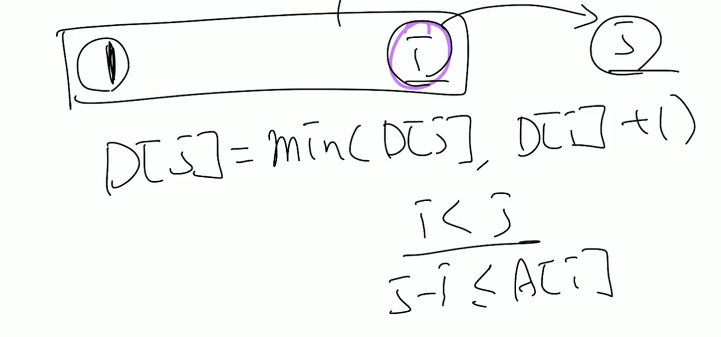
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#define len 1500001
using namespace std;
int d[1001];
int main(void) {
freopen("input.txt", "r", stdin);
int t;
cin >> t;
vector<int> a(t);
memset(d, -1, sizeof(d));
for (int i = 0; i < t; ++i) {
cin >> a[i];
}
d[0] = 0;
for (int i = 0; i < t-1; ++i) {
if (d[i] == -1) continue;
for (int j = 1; j <= a[i]; ++j) {
if (i + j >= t) break;
if (d[i + j] == -1 || d[i + j] > d[i] + 1) {
d[i + j] = d[i] + 1;
}
}
}
cout << d[t-1] << '\n';
}15486 퇴사 2 / 14501 퇴사
퇴사2 문제는 점프점프와 다르게 이동할 수 있는 거리 이내라는 제약 조건이 없기 때문에 o(N) 만으로도 문제를 풀 수 있다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#define len 1500001
using namespace std;
int d[len] = { 0 };
int main(void) {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
freopen("input.txt", "r", stdin);
int n;
cin >> n;
vector<int> t(n+1);
vector<int> p(n+1);
for (int i = 0; i < n; ++i) {
cin >> t[i] >> p[i];
}
for (int i = 0; i < n; ++i) {
if(i+t[i]<=n) d[i + t[i]] = max(d[i + t[i]], d[i] + p[i]);
d[i + 1] = max(d[i], d[i + 1]);
}
cout << d[n] << '\n';
}여기에서 중요한 것은 이동할 수 있는 거리가 정해져 있다는 것이다. 그렇기 때문에 2579번 계단오르기와는 다른 풀이법이 가능하다.
계단오르기는 갈 수 있는 거리가 유동적이다. 하다못해 점프점프처럼 경우의 수를 구할 수 있는 것도 아니다.
비슷한 문제
2839 설탕배달
문제 유형은 비록 수학이지만 점프점프 유형으로 풀 수 있다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#define ll long long
#define len 1001
using namespace std;
int d[5001];
int main(void) {
//freopen("input.txt", "r", stdin);
int n;
scanf("%d", &n);
memset(d, -1, sizeof(d));
d[3] = d[5] = 1;
for (int i = 3; i <= n; ++i) {
if (d[i] != -1) {
if (i + 3 <= n && (d[i + 3] == -1
|| d[i + 3] > d[i] + 1)) {
d[i + 3] = d[i] + 1;
}
if (i + 5 <= n && (d[i + 5] == -1
|| d[i + 5] > d[i] + 1)) {
d[i + 5] = d[i] + 1;
}
}
}
cout << d[n] << '\n';
}1890 점프
크게 다르지 않고 문제에서 계속해서 이동을 구해주면 된다.
import sys
sys.stdin = open('input.txt','r')
t = int(input())
a = [list(map(int,input().split()))for _ in range(t)]
d = [[0] * t for _ in range(t)]
d[0][0] = 1
for i in range(t):
for j in range(t):
if(a[i][j]==0): continue
if(i+a[i][j]<t):
d[i+a[i][j]][j] +=d[i][j]
if(j+a[i][j]<t):
d[i][j+a[i][j]]+=d[i][j]
print(d[t-1][t-1])
2. 영토 확장 유형 : 쿼리문제
문제에 뭔가가 있음 (ex> 수열) 그리고 여기에 무언가를 해주어야 답을 구해줄 수 있는 구조
문제
10942 팬리드롬?

한마디로 '기러기'
방법 1
수열에 데이터를 저장하고
또 하나의 수열을 준비하되 그 수열에는 원래 수열의 데이터를 뒤집은 데이터를 저장한다.
이게 왜 dp 문제 인가?
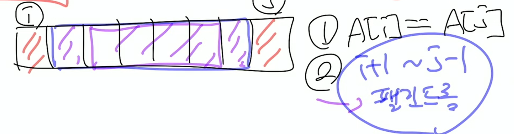
이와 같이 맨 끝과 끝을 비교한다음 더 작은 수열의 끝과 끝과 비교하기 때문에 결과적으로 다이나믹 프로그래밍이라고 생각할 수 있다.
실재 문재를 풀때는 중앙부분부터 한칸 씩 늘리어가면서 풀면 된다.
점화식을 세워 보면
D[i][j] = A[i]-A[j] 가 팬린드롬이면 1, 아니면 0
초기화 하면
길이가 1인 부분 수열은 무조건 팬린드롬이다.
길이가 2인 부분 수열은 두 수가 같을 때만 팬린드롬이다.
D[i][i+1] =1 (A[i] = A[i+1])
D[i][i+1] =0 (A[i] != A[i+1])
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <functional>
#include <vector>
#include <algorithm>
#include <queue>
#include <deque>
#include <stack>
#include <cstring>
#define ll long long
#define len 2001
using namespace std;
int a[len];
int d[len][len];
int go(int s, int e) {
if (s == e) {
return 1;
}
else if (s + 1 == e) {
if (a[s] == a[e]) return 1;
else return 0;
}
if (d[s][e] != -1) {
return d[s][e];
}
if (a[s] != a[e]) {
return d[s][e] = 0;
}
else {
return d[s][e] = go(s + 1, e - 1);
}
}
int main(void) {
freopen("input.txt", "r", stdin);
int n;
scanf("%d", &n);
for (int i = 0; i < n; ++i) {
scanf("%d", &a[i]);
}
memset(d, -1, sizeof(d));
int t;
scanf("%d", &t);
while (t--) {
int s, e;
scanf("%d %d", &s, &e);
printf("%d\n", go(s-1, e-1));
}
}3. 독립 유형 : 1,2,3 더하기 4
키워드
독립된 모든 경우를 구하라는 형태의 문제로
하나의 값을 가지고 나올 수 있는 모든 경우를 구하고 그 다음 값을 가지고 모든 경우를 구하는 식으로 확장해 나가면 된다.
문제
15989 1, 2, 3 더하기 4
독립된 경우만을 구하는 것이기 때문에 점화식을 사용하기 보다는 메커니즘을 고안해야 한다.
보통 이런경우 많이 사용하는 것이 1에 대해서 모두 구하고 2에 대해 모두 구하고 3에 대해 모두 구하는 순서로 하나의 대표되는 케이스만 구하는 방법이 존재한다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#define len 1001
using namespace std;
int d[10001];
int main(void) {
freopen("input.txt", "r", stdin);
memset(d, 0, sizeof(d));
int t;
scanf("%d", &t);
d[0] = 1;
for (int j = 1; j <= 3; ++j) {
for (int i = 1; i <= 10000; ++i) {
if (i - j >= 0) {
d[i] += d[i - j];
}
}
}
while (t--) {
int n;
scanf("%d", &n);
cout << d[n] << '\n';
}
}비슷한 유형
동전1 2293
import sys
sys.stdin = open('input.txt','r')
t,m = map(int,input().split())
a = [int(input()) for _ in range(t)]
d = [0] * (m+1)
d[0] = 1
for i in range(t):
for j in range(m+1):
if((j-a[i])>=0):
d[j] += d[j-a[i]]
print(d[m])동전2 2294
import sys
sys.stdin = open('input.txt','r')
t,m = map(int,input().split())
a = [int(input()) for _ in range(t)]
d = [-1] * (m+1)
d[0] = 0
for i in range(t):
for j in range(m+1):
if((j-a[i])>=0 and d[j-a[i]]!=-1):
if(d[j] == -1 or d[j]>d[j-a[i]]+1):
d[j] = d[j-a[i]]+1
print(d[m])4. DP 파일 합치기 : 연속 문제
키워드
연속된다라는 표현이 들어가 있다면 DP로 풀 수 있는 가능성이 높아 진다.
그게 아니더라도 문제가 연속이 아니면 풀리지 않는다면 그거 역시 DP 연속 문제에서 파일합치기 문제라고 볼 수 있다.
왜냐하면 마지막으로 나올 수 있는 케이스가 정해져 있기 때문이다.
문제
11066 파일합치기
연속되기 때문에 DP로 풀 수 있다.
또한 마지막을 생각해보면

이렇게 4가지 방법밖에 존재하지 않기 때문에 DP를 풀기에 안성맞춤이다.
또 한가지 생각해 보아야하는 것이 A1 to A3와 A3 to A5는 갯수는 같을지 언정 경우가 다른 것이기 때문에 시작위치와 끝위치를 기준으로 경우의 수를 표현해 줄 수 있다.
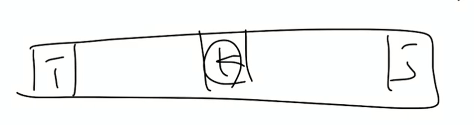
i부터 j까지 합치어 졌다는 것은 중간의 k번째까지 합치어 졌다는 것인데 k가 무엇인지 모른다.
DP에서 모르는 것은 매우 좋은 정보이기 때문에 이때 DP로 푸는 것을 확신할 수 있다.
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#define ll long long
#define len 1001
using namespace std;
int a[501] = { 0 };
int d[501][501] = { 0 };
int go(int i, int j) {
if (i == j) return 0;
if (d[i][j] > 0) return d[i][j];
int sum = 0;
for (int s = i; s <= j; ++s) {
sum += a[s];
}
for (int k = i; k <= j - 1; ++k) {
int tmp = go(i, k) + go(k + 1, j) + sum;
if (d[i][j] == -1 || d[i][j] > tmp) {
d[i][j]= tmp;
}
}
return d[i][j];
}
int main(void) {
freopen("input.txt", "r", stdin);
int t;
scanf("%d", &t);
while (t--) {
memset(d, -1, sizeof(d));
int n;
scanf("%d", &n);
for (int i = 0; i < n; ++i) {
scanf("%d ", &a[i]);
}
cout<<go(0, n - 1)<<'\n';
}
}비슷한 유형
11049 행렬 곱셈 순서
top-down 방식에서는 초기값이 곧 예외 경우 즉 함수를 탈출하는 경우이기 때문에 함수의 초기화 경우를 생각해 보면 3가지가 있다.
- 계산하는 행렬의 s와 e가 같은 경우 return 0
- 계산하는 행렬의 s+1 와 e가 같은 경우 return a[s].first a[e].first a[e].second;
- if(d[s][e]>0) return d[s][e];
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#define ll long long
#define len 1001
using namespace std;
pair<int, int> a[501];
ll d[501][501] = { 0 };
int go(int s, int e) {
if (d[s][e] > 0) return d[s][e];
if (s == e) return 0;
if (s + 1 == e) return a[s].first * a[e].first * a[e].second;
for (int k = s; k <= e - 1; ++k) {
ll tmp = go(s, k) + go(k + 1, e);
if (d[s][e] == -1 ||
d[s][e] > tmp + a[s].first * a[k].second * a[e].second) {
d[s][e] =
tmp + a[s].first * a[k].second * a[e].second;
}
}
return d[s][e];
}
int main(void) {
freopen("input.txt", "r", stdin);
int t;
scanf("%d", &t);
for (int i = 0; i < t; ++i) {
scanf("%d %d\n", &a[i].first, &a[i].second);
}
memset(d, -1, sizeof(d));
cout << go(0, t - 1) << '\n';
}5. 제한 유형 : O(2^n) -> O(NM) 의 크기를 가지는 문제
키워드
문제를 그냥 보면 시간복잡도가 매우 커 보이지만
실재로는 제한이 존재하기 때문에 해당 제한을 활용하면 문제를 풀 수 있는 유형
문제
문제를 푸는 알고리즘에서
1. 어떤 것을 넣고 뺄지 모르겠다.(경우는 2가지 인데 O(2^n) 이 나온다.)
2. 삽입삭제를 결정할 수 있다. => 물건이 반드시 연속하지 않아도 된다.
12865 평범한 배낭

이 문제는 매우매우 중요하니 다시한번 풀어보자
#define _CRT_SECURE_NO_WARNINGS
#define _USE_MATH_DEFINES
#include <iostream>
#include <cstring>
#include <cstdio>
#include <functional>
#include <algorithm>
#include <cstdlib>
#include <vector>
#include <ctime>
#define ll long long
#define len 1001
using namespace std;
int w[101];
int v[101];
int d[101][100001];
int main(void) {
freopen("input.txt", "r", stdin);
int n, k;
scanf("%d %d", &n, &k);
for (int i = 1; i <= n; ++i) {
scanf("%d %d", &w[i], &v[i]);
}
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= k; ++j) {
d[i][j] = d[i - 1][j];
if(j-w[i]>=0) d[i][j] = max(d[i - 1][j - w[i]] + v[i], d[i][j]);
}
}
int max=0;
for (int i = 1; i <= n; ++i) {
if (d[i][k] > max) max = d[i][k];
}
cout << max;
}만약 이 문제를 1차원 배열로 풀게 된다면 i번째 물건이라는 정보는 필요하지 않기 때문에 점화식을 다음과 같이 간단하게 만들 수 있다.
d[j] = max(d[j-w[i]]+v[i],d[j])
하지만 이 문제를 이렇게 풀경우 문제점이 하나 있는데
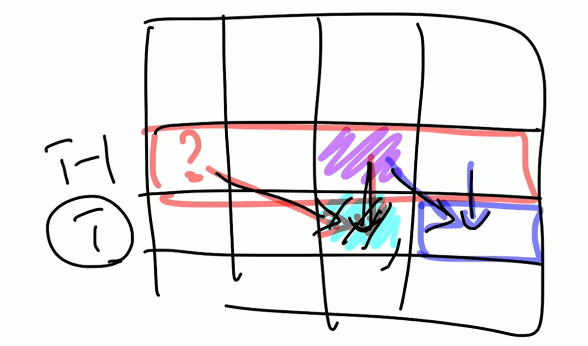
원래 값을 참조하는 위치가 보라색 위치여야 하지만 위의 점화식을 보면 파란색의 위치를 참조하고 있기 때문에 아무 값도 없는 d[j]가 이용될 수 있다.
그렇기 때문에 이러한 문제를 해결하기 위해서 배열을 뒤에서 부터 채워 중복을 없애주는 방법을 사용할 수 있다.
1495 기타리스트
한 번 음악을 칠때마다 경우의 수가 2개씩 늘어나는 O(2^n) 형태의 문제이다.
하지만 100개의 음이 존재하기 때문에 이 모든 경우를 시간안에 도는 것은 불가능하다.
그렇기 때문에 제약조건인 M을 넘을 수 없다는 것과 필요한 범위만큼만 이동하면 된다는 O(NM) 방법을 이용한 문제풀이를 해주어야 한다.

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <functional>
#include <vector>
#include <algorithm>
#include <queue>
#include <deque>
#include <stack>
#include <cstring>
#define ll long long
#define len 2001
using namespace std;
int n, s, m;
int a[101];
bool d[101][1001];
int main(void) {
freopen("input.txt", "r", stdin);
scanf("%d %d %d", &n, &s, &m);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
}
d[0][s] = true;
for (int i = 0; i <= n; ++i) {
for (int j = 0; j <= m; ++j) {
if (d[i][j]) {
if (j + a[i+1] <= m) {
d[i + 1][j + a[i + 1]] = true;
}
if (j - a[i+1] >= 0) {
d[i + 1][j - a[i + 1]] = true;
}
}
}
}
int ans = -1;
for (int i = 0; i <= m; ++i) {
if (d[n][i]) ans = i;
}
printf("%d\n", ans);
}python
import sys
sys.stdin = open('input.txt','r')
n,s,m=map(int,input().split())
d=[[False]*1001 for _ in range(101)]
a=[0]+list(map(int,input().split()))
d[0][s] = True
for i in range(n):
for j in range(m+1):
if(d[i][j]):
if(j+a[i+1]<=m):
d[i+1][j+a[i+1]]=True
if(j-a[i+1]>=0):
d[i+1][j-a[i+1]]=True
ans = -1
for i in range(m+1):
if(d[n][i]): ans = i
print(ans)12869 뮤탈리스크

뮤탈리스크 문제인데
만약 scv 3기 모두 체력 60이라고 하면
뮤탈리스크는 O(61^3)=O(226,981) 이라는 풀만한 숫자의 갯수가 생기게 된다.
거기에다가 이미 구해낸 scv 체력별 값을 저장하여 큰 문제에서 작은 문제로 풀 수 있기 때문에 DP문제라고 생각할 수 있다.
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <functional>
#include <vector>
#include <algorithm>
#include <queue>
#include <deque>
#include <stack>
#include <cstring>
#define ll long long
#define len 2001
using namespace std;
int a[3];
int d[61][61][61];
int attack(int i, int j, int k) {
//제기로 짜기 때문에 음수를 처리하기 쉬움
if (i < 0) return attack(0, j, k);
if (j < 0) return attack(i, 0, k);
if (k < 0) return attack(i, j, 0);
//이미 파괴된 상태이기 때문에 구지 추가 공격하지 않음
if (i == 0 && j == 0 && k == 0) return 0;
//해당 인덱스의 값을 우선 받은 다음 시작
int &ans = d[i][j][k];
if (ans != -1) return ans;
ans = 1000000;
vector<int> w = { 1,3,9 };
//모든 경우를 돌면서 최소의 경우를 저장하기
do {
int tmp = attack(i - w[0], j - w[1], k - w[2]);
if (ans > tmp) {
ans = tmp;
}
} while (next_permutation(w.begin(), w.end()));
ans += 1;
return ans;
}
int main(void) {
freopen("input.txt", "r", stdin);
int t;
cin >> t;
for (int i = 0; i < t; ++i) {
cin >> a[i];
}
memset(d, -1, sizeof(d));
cout << attack(a[0], a[1], a[2]) << '\n';
}10422 괄호
이 문제가 DP인 이유는 이미 만든 괄호에 대해서는 추가적인 괄호를 연산할 필요가 없기 때문이다.
비슷한 유형
5557 1학년
import sys
sys.stdin = open('input.txt','r')
t = int(input())
a = list(map(int,input().split()))
d = [[0] * 21 for _ in range(100)]
d[0][a[0]] = 1
goal = a[- 1]
for i in range(1,t - 1):
for j in range(21):
if(j + a[i] <= 20):
d[i][j] += d[i - 1][j + a[i]]
if(j - a[i] >= 0):
d[i][j] += d[i - 1][j - a[i]]
print(d[t - 2][goal])
6. 3차원 이상 배열 유형 : ABC
https://dojang.io/mod/page/view.php?id=2297
d = [[[[False]*436 for k in range(31)]
for j in range(31)] for i in range(31)]정리하자면 for i in range 반복
이때 가장 안쪽에 들어간 게 배열에서는 가장 마지막 부분(행,열,높이,깊이 순)
키워드
알고리즘
문제
12969 ABC
import sys
sys.stdin = open('input.txt','r')
d = [[[[False]*436 for k in range(31)]
for j in range(31)]for i in range(31)]
n,k=map(int,input().split())
ans=''
def go(i,a,b,p):
if(i==n):
if(p==k): return True
else: return False
if(d[i][a][b][p]): return False
d[i][a][b][p]=True
global ans
temp = ans
ans = temp+'A'
if(go(i+1,a+1,b,p)): return True
ans = temp+'B'
if(go(i+1,a,b+1,p+a)): return True
ans = temp+'C'
if(go(i+1,a,b,p+a+b)): return True
return False
if(go(0,0,0,0)): print(''.join(ans))
else: print("-1")