시.이.바 알고리즘 공부법 연구중

시 : 시간복잡도

이 : 입력 크기

바 : 바깥 경우(코너 케이스)

알고리즘 문제를 푼다는 것이 어떤것을 공부하는 것인지에 대해 연구중에 있음

PS 를 푼다는 것의 목적은

1. 짧은 시간안에 제한시간내에 풀리는 알고리즘 구현(이게 가장 중요한게 정보 올리피아드도 절반 이상은 골실 문제이고 간혹가다가 플래티넘이 나오는 형태임 그리고 구현이 쉬운 알고리즘일 수록 오랜시간이 걸림 하지만 우리가 중요한 것은 빠른 시간안에 문제의 풀이법을 제시하는 것이지 더 짧은 시간안에 풀리는 문제 풀이법을 구현하는 것이 아님 그렇기 때문에 오랜시간이 걸리더라도 더 적은 시간안에 구현되는 문제가 풀리는 알고리즘 구현이 중요함.)

2. 풀 수 있는 문제는 100% 풀어내기(또한 구지 다이아 문제를 도전해서 성공해 보았자 알고리즘 대회에서는 브실골 문제 많이 푼사람 못이김 이는 곧 브실골 문제는 무조건 100% 풀어낼 수 있어야 한다는 거임. 입문자를 비롯한 대다수의 고급 PS Solver 가 된다는 것은 곧 브실골 문제를 실수 없이 구현해 낼 수 있다는 것을 의미한다고 생각함)

그래서 알고리즘을 총 5개의 영역으로 구분함

기준은 종만북이고 solved.ac 와 code.plus에 나와 있는 목차를 기준으로 종합하였음.

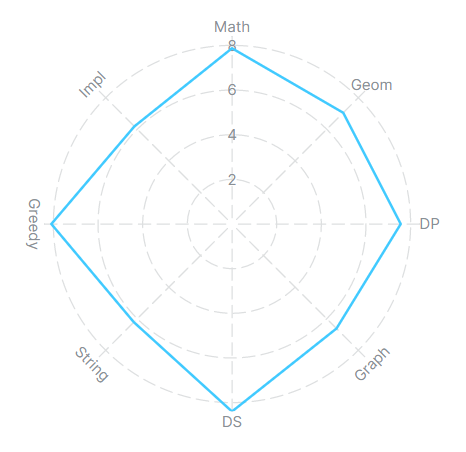
자료구조 ㅇ - 스택, 큐, 덱, 선형, 유니온 파인드, 힙, BST, 문자열 알고리즘(KMP, TRIE, AHO-CORASICK), 비트마스크, 부분 합

수학 - 수치 해석, 정수론 기하 알고리즘

구현

• DP - 그리디

• 브루트 포스 - N과 M, 순열, 재귀, 비트마스크

• 분할정복 - 정렬 ,이분 탐색, 조합 탐색

그래프 - BFS/DFS, DAG와 위상 정렬, MST, 벨만포드, 다익스트라, 플로이드와 SPFA, 최소 스패닝 트리(크루스칼), 네트워크 유량(포드-풀커슨 알고리즘)

트리 ㅇ - 세그먼트 트리, 펜윅 트리, 누적합, 이진검색트리, 우선순위 큐와 힙, 구간 트리, 트라이, 상호 배타적 집합

보면 알겠지만 그렇게 많지 않음. 또한 결국에는 자료구조의 연장선인 것을 알 수 있음.

계속 연구하겠뜸

https://plzrun.tistory.com/entry/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EB%AC%B8%EC%A0%9C%ED%92%80%EC%9D%B4PS-%EC%8B%9C%EC%9E%91%ED%95%98%EA%B8%B0