가중치 그래프 구현 및 탐색

백준 1753번을 Java를 이용해 풀어보았다. 가중치 그래프를 구현해보기는 처음이었고 다익스트라 알고리즘도 처음이어서 새롭게 배우는 시간이었다. ArrayList와 LinkedList의 차이도 글로만 배웠지 실제로 체감한 것은 오늘이 처음이었다. 문제를 살펴보며 후술하겠다.

문제 링크 첨부한다.
https://www.acmicpc.net/problem/1753

---

가중치 그래프 구현

가중치 그래프를 구현하기 위해서는 다음 정보들을 저장해야 한다.

1. start -> end // 시작점과 도착점
2. weight // 가중치

문제에서는 시작점과 도착점, 그리고 그 간선의 가중치를 입력값으로 준다. 이 정보들을 ArrayList[] 에 저장해야 한다. 이를 코드로 표현하면 다음과 같다.

int V = Integer.parseInt(stk.nextToken()); // 정점 개수
int E = Integer.parseInt(stk.nextToken()); // 간선 개수

/** 간선 가중치 입력 받기 */
ArrayList<Node>[] edges = new ArrayList[V+1];
for (int i = 0; i <= V; i++) edges[i] = new ArrayList<>();
int a, b, cost;
for (int i = 0; i < E; i++) { // 간선 가중치 정보 입력 받기
       stk = new StringTokenizer(bfr.readLine());
       a = Integer.parseInt(stk.nextToken());
       b = Integer.parseInt(stk.nextToken());
       cost = Integer.parseInt(stk.nextToken());
       edges[a].add(new Node(b, cost));
}

static class Node implements Comparable<Node> {
        int end;
        int cost;

        Node(int end, int cost) {
            this.end = end;
            this.cost = cost;
        }

        @Override
        public int compareTo(Node next){ // 후에 왜 필요한지 설명하겠다
            return this.cost - next.cost;
        }
    }

위와 같이 돌리면 edges의 특정 인덱스(i)에는 i번째 정점에 연결돼있는 정점들 정보가 저장된다. 가중치가 존재하기 때문에 그냥 정점 번호만 저장해줄 것이 아니라, weight 정보를 담은 Node라는 클래스를 정의해서 Node들을 저장해줘야 하는 것이다.

---

최소 비용 구하기 위한 요소들

이 문제에서는 시작점으로 주어진 정점으로부터 나머지 모든 정점까지의 최소 비용을 구해줘야 하기 때문에 총 V개의 비용들을 담을 수 있는 int[] distance가 필요하다.

그리고 처음부터 미리 세팅하고 들어갈 수 있는 정보는, 시작점->시작점의 distance값은 0으로 저장하고 들어갈 수 있다. 이를 코드로 표현하면 다음과 같다.

/** 최소 비용 거리 정보를 담아줄 배열 초기화 */
int[] distance = new int[V + 1]; // 출발점으로부터 모든 노드까지의 최소 거리를 저장해줄 int 배열
for (int i = 0; i < V + 1; i++) distance[i] = Integer.MAX_VALUE;
distance[K] = 0;

다익스트라 알고리즘을 적용해서 더 작은 비용이 나오면 갱신해줘야 하기 때문에 세팅은 모든 비용값을 Integer.MAX_VALUE로 세팅해주고 들어가야 한다.

---

다익스트라 알고리즘 적용

최소 비용을 찾아주기 위한 모든 세팅이 마무리 됐다. 이제 다익스트라 알고리즘이 무슨 짓을 하는지 살펴보자.

다익스트라 알고리즘을 구현하기 위해서 두 가지 접근 방식이 있는 것을 배웠다. boolean[] visited 배열을 이용하거나 우선 순위 큐를 이용할 수도 있다.

두 가지 방식을 모두 이용해 풀이해봤는데 이번 문제에서는 시간 복잡도 때문에 우선 순위 큐를 이용해서 제출했다.

그러면 어떤 로직으로 돌아가는지 한 번 살펴보자.

1. 시작점 자기 자신을 큐에 넣어주고 시작하기
2. 큐에 들어있는 노드 꺼내주기 ( Node cur = q.poll(); )
3. 정점 cur까지의 최소 비용이 cur.cost 보다 작으면 그냥 넘기기 // 이미 있는 최소비용이 더 작으니까 갱신해줄 필요가 없음
4. 3에서 걸리지 않았으면, cur 주변 노드들을 쭉 순회하며 next 노드들에 대해 살펴보자. 정점 next까지의 최소 비용보다 (cur.cost + next.cost)가 더 작으면 정점 next 까지의 최소 비용을 (cur.cost + next.cost) 로 갱신해주자.
5. 갱신했으면 new Node(next.end, cur.cost+next.cost)를 큐에 새롭게 넣어주자

위의 작업을 코드로 표현하면 다음과 같다.

/** 다익스트라 알고리즘 적용 ( 우선순위 큐 이용 ) */
PriorityQueue<Node> q = new PriorityQueue<>();
q.offer(new Node(K, 0));

while(!q.isEmpty()){
       Node cur = q.poll();
       if(distance[cur.end] < cur.cost)    continue; // 이미 최소비용을 만족하니까 패스

       for(int i=0; i<edges[cur.end].size(); i++){ // 현재 정점에 연결돼있는 정점들 살펴보며 
           Node next = edges[cur.end].get(i);
           if(distance[next.end] > cur.cost + next.cost) { // 새롭게 최소 비용을 갱신해줄 수 있으면 해주자
               distance[next.end] = cur.cost + next.cost;
               q.offer(new Node(next.end, distance[next.end]));
           }
       }
}

---

정답 출력

모든 정점에 대해 최소 비용 배열 값들을 출력해주면 되는데 만약 끝까지 Integer.MAX_VALUE가 갱신되지 않은, 즉 시작점으로부터 도달할 수 없는 정점들에 대해서는 INF를 출력해주고 나머지는 최소 비용 값을 출력해주면 된다.

/** 정답 출력 */
for (int i = 1; i < V + 1; i++) {
       if (distance[i] == Integer.MAX_VALUE)
           bfw.write("INF\n");
       else
            bfw.write(distance[i] + "\n");
}
bfw.close();

---

위의 모든 코드들을 합치면 다음과 같다. 내가 제출한 코드다.

import java.io.*;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.PriorityQueue;
import java.util.StringTokenizer;

public class boj1753 {
    public static void main(String[] args) throws IOException {
        BufferedWriter bfw = new BufferedWriter(new OutputStreamWriter(System.out));
        BufferedReader bfr = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer stk = new StringTokenizer(bfr.readLine());
        int V = Integer.parseInt(stk.nextToken()); // 정점 개수
        int E = Integer.parseInt(stk.nextToken()); // 간선 개수
        int K = Integer.parseInt(bfr.readLine());

        /** 간선 가중치 입력 받기 */
        ArrayList<Node>[] edges = new ArrayList[V+1];
        for (int i = 0; i <= V; i++) edges[i] = new ArrayList<>();
        int a, b, cost;
        for (int i = 0; i < E; i++) { // 간선 가중치 정보 입력 받기
            stk = new StringTokenizer(bfr.readLine());
            a = Integer.parseInt(stk.nextToken());
            b = Integer.parseInt(stk.nextToken());
            cost = Integer.parseInt(stk.nextToken());
            edges[a].add(new Node(b, cost));
        }

        /** 각 노드 방문 여부 체크해줄 배열 초기화 */
//        boolean[] visited = new boolean[V + 1]; // 방문 여부 체크해줄 boolean 배열

        /** 다익스트라 알고리즘 적용 ( visited 배열 이용 ) */
//        for (int i = 0; i < V; i++) {
//            int curIdx = 0;
//            int valueOfCurIdx = Integer.MAX_VALUE;
//
//            for (int j = 1; j <= V; j++) {
//                if (!visited[j] && distance[j] < valueOfCurIdx) {
//                    curIdx = j;
//                    valueOfCurIdx = distance[j];
//                }
//            }
//            visited[curIdx] = true;
//
//            for (int j = 0; j < list.get(curIdx).size(); j++) {
//                Node adjNode = list.get(curIdx).get(j);
//                if (distance[adjNode.end] > valueOfCurIdx + adjNode.cost) {
//                    distance[adjNode.end] = valueOfCurIdx + adjNode.cost;
//                }
//            }
//        }

        /** 최소 비용 거리 정보를 담아줄 배열 초기화 */
        int[] distance = new int[V + 1]; // 출발점으로부터 모든 노드까지의 최소 거리를 저장해줄 int 배열
        for (int i = 0; i < V + 1; i++) distance[i] = Integer.MAX_VALUE;
        distance[K] = 0;

        /** 다익스트라 알고리즘 적용 ( 우선순위 큐 이용 ) */
        PriorityQueue<Node> q = new PriorityQueue<>();
        q.offer(new Node(K, 0));

        while(!q.isEmpty()){
            Node cur = q.poll();
            if(distance[cur.end] < cur.cost)    continue;

            for(int i=0; i<edges[cur.end].size(); i++){
                Node next = edges[cur.end].get(i);
                if(distance[next.end] > cur.cost + next.cost) {
                    distance[next.end] = cur.cost + next.cost;
                    q.offer(new Node(next.end, distance[next.end]));
                }
            }
        }

        /** 정답 출력 */
        for (int i = 1; i < V + 1; i++) {
            if (distance[i] == Integer.MAX_VALUE)
                bfw.write("INF\n");
            else
                bfw.write(distance[i] + "\n");
        }
        bfw.close();
    }

    static class Node implements Comparable<Node> {
        int end;
        int cost;

        Node(int end, int cost) {
            this.end = end;
            this.cost = cost;
        }

        @Override
        public int compareTo(Node next){
            return this.cost - next.cost;
        }
    }
}

---

ArrayList와 LinkedList 의 차이

글 서두에 써둔 두 녀석의 차이를 체감했다는 부분은 다음 코드에서다.

for(int i=0; i<edges[cur.end].size(); i++){
           Node next = edges[cur.end].get(i); // 바로 여기!!
           if(distance[next.end] > cur.cost + next.cost) {
               distance[next.end] = cur.cost + next.cost;
               q.offer(new Node(next.end, distance[next.end]));
           }
}

다익스트라 알고리즘 적용 부분에서 현재 정점으로부터 연결된 정점들에 대해 탐색할 때, edges[cur.end].get(i)에서 바로 get 메소드가 문제였다!!

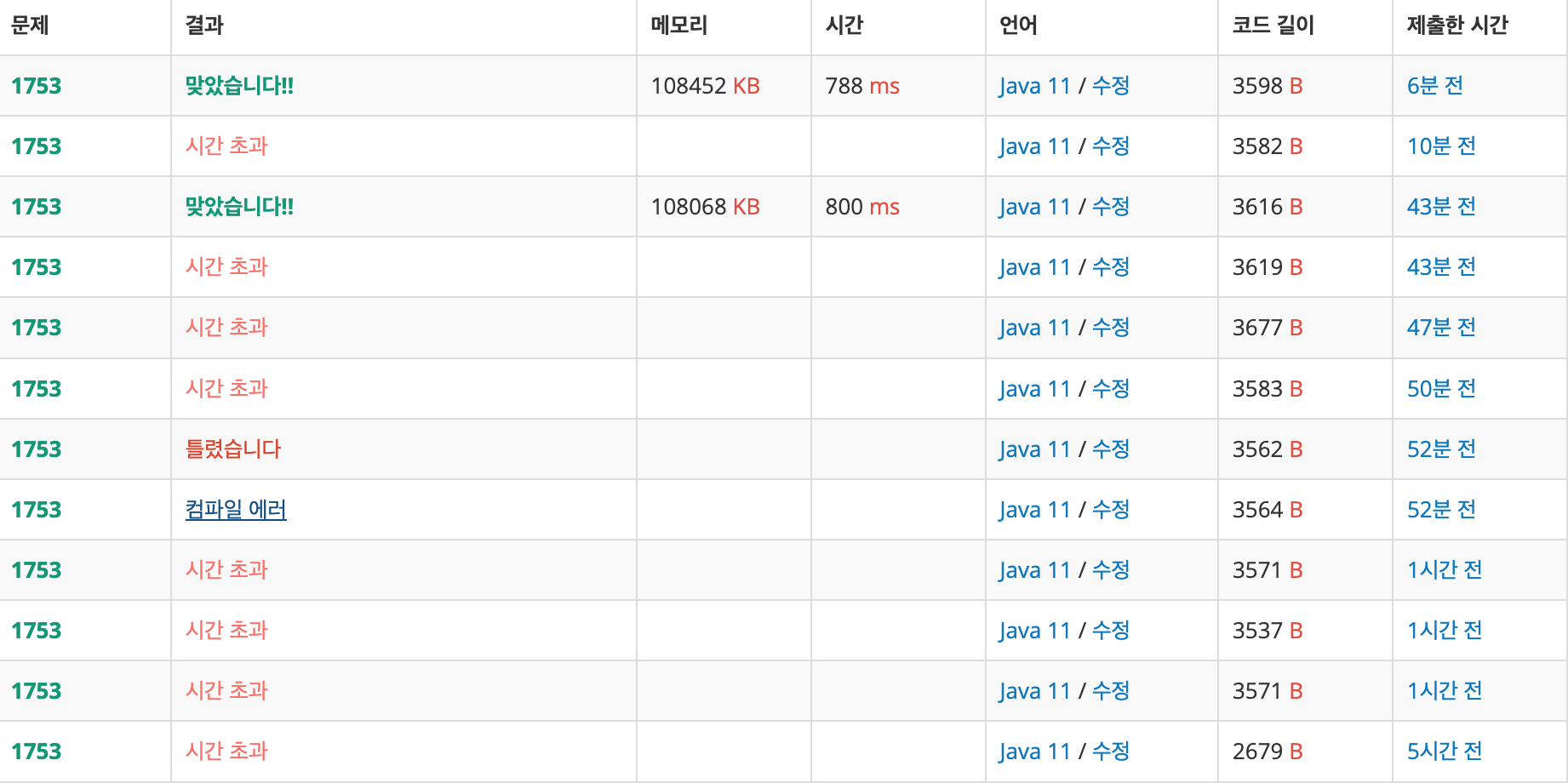
난 처음에 ArrayList가 아닌 LinkedList를 썼는데 LinkedList를 쓰면 get, set 메소드를 사용할 때 O(n)의 시간 복잡도가 된다. 하지만 ArrayList는 O(1)의 시간 복잡도이기 때문에 특정 인덱스로 갈 때는 ArrayList가 유리하다. 저 한 줄 때문에 내가 1시간 반 가량 헤맸다...

계속 로직이 문제인가 싶어서 아무리 다른 사람들의 코드와 비교해봐도 모든 게 맞아 떨어지는데 뭔가 싶어서 자료구조가 문제일까? 하고 살펴봤더니 다른 사람들은 ArrayList를 쓴 걸 보고 무슨 차이가 있을까 해서 봤더니 이미 다 공부했던 내용인데 실제로 그 차이를 체감해본 적이 없어서 눈치 채지 못했던 것이다.

역시 인생은 실전이다 ㅈ만아!