[알고리즘 스터디] 그래프

그래프

• 정점(V)과 간선(E)으로 이루어진 자료구조
• 트리와 다른점은 사이클이 존재할 수 있고 간선의 방향이 양방향일 수 있다.

그래프 순회 방법

BFS, DFS

그래프를 자료구조로 표현하는 방법 3가지

1. 인접행렬 : 공간낭비 너무 심함
2. 인접리스트 : 시간낭비 너무 심함
   3. 간선리스트 : 간선(엣지)를 중심으로 표현하는 방법.
   
   

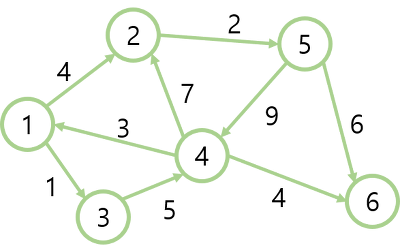
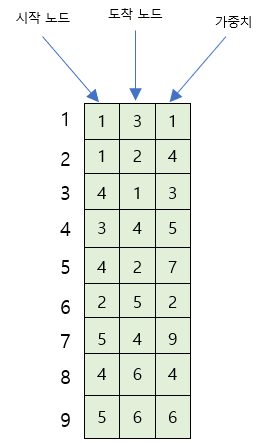
" [시작노드, 도착노드, 가중치] " 자료구조를 리스트나 배열형태로 저장하여 그래프 표현

이 때 사용하는 알고리즘으로 대표적인게 프림 알고리즘, 크루스칼 알고리즘

최소 신장 트리 (MST; Minimum Spanning Tree)

• spanning Tree(스패닝 트리,신장 트리) : 그래프의 모든 정점을 연결하는 최소 연결 부분 그래프 입니다.
  = 그래프에서 일부 간선만을 선택해서 만든 트리
• minimum spanning Tree(최소 신장 트리) : spanning Tree 중에서 사용된 간선들의 가중치 합이 최소인 트리
• MST의 조건

1. 본래 그래프의 모든 노드 포함
2. 간선의 가중치의 합이 최소
3. 모든 노드가 서로 연결
4. 트리의 속성 만족 (사이클 없음)

• MST를 찾는 방법: 크루스칼 알고리즘, 프림 알고리즘

• 간선이 적을 땐 크루스칼 알고리즘, 간선이 많을 땐 프림 알고리즘

크루스칼 알고리즘

• 모든 간선에 대해 가중치가 가장 작은것들을 우선으로 하여 MST의 조건을 만족할 수 있는 V-1개의 간선을 선택하는 방법
• 아직 선택되지 않은 간선들 중에 가중치가 가장 작으면서 사이클을 만들지 않는 간선을 선택

동작원리

1. 모든 간선들의 가중치를 오름차순으로 정렬
2. 가중치가 가장 작은 간선 선택
3. 위에서 선택한 간선이 연결하려는 2개의 노드가 서로 연결되지 않은 상태면 2개의 노드를 연결
4. 위 과정 반복

예제)

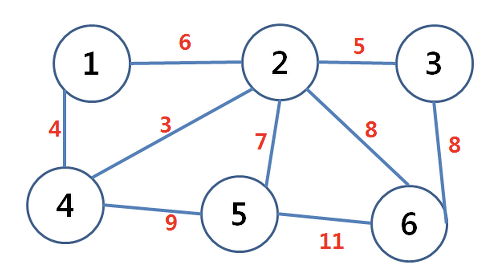
parent[] = {1,2,3,4,5,6}
sum=0
bool isSameParent

1. 모든 간선들의 가중치를 오름차순으로 정렬
   

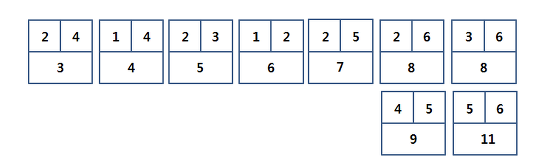
2. 가중치가 가장 작은 간선 선택
   정점2와 정점4가 연결됐는지 보고 isSameParent(2,4)) false이면, sum에 더해줍니다. 그리고 정점2와 정점4를 연결(union)해 줍니다.
   

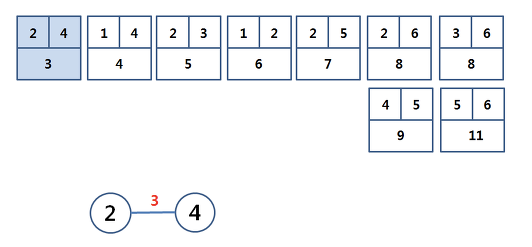
sum = 3
parent[4]=2가 됩니다. ( parents[] = {1,2,3,2,5,6} )

3. 그다음 가중치가 낮은(4) 간선을 선택합니다. 정점 1과 4가 연결됬는지 보고(isSameParent(1,4)) false이면, sum에 더해줍니다. 그리고 정점 1과 4를 연결(union)해줍니다.
   sum = 7
   parent[2]=1 -> 이게 중요함. parent[4]=1이되는게 아니라 4의부모인 2에 접근해서 parent[2]=1이됨. ( parents[] = {1,1,3,2,5,6} )
   

이렇게 연결해나가면

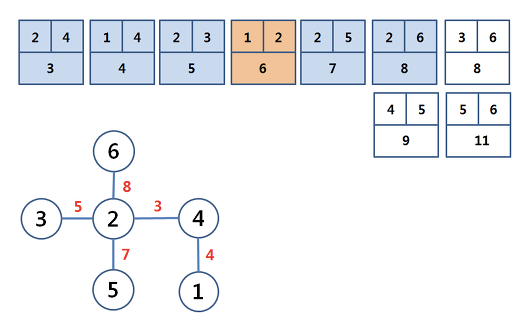
모든 정점이 연결되게 된다.

프림 알고리즘

• 크루스칼과 마찬가지로 MST(최소신장트리)를 구현하는 한 방법으로, 다익스트라(Dijkstra) 알고리즘과 유사하게 동작한다.
• 시작 정점을 기준으로 가중치가 가장 작은 간선과 연결된 정점을 선택하며 트리를 확장시켜나가는 방법이다.
  각 정점들은 인접한 정점 중 최소비용으로 이동가능한 정점을 선택하여 큐에 추가한다.
• 우선순위 큐를 이용하여 임의의 정점부터 인접한 정점을 가중치 기준으로 정렬한다.
• 선택된 정점그룹 / 선택되지 않은 정점그룹으로 나누어 생각.

동작과정

1. 임의의 정점을 선택
2. 이 정점에서 다른 정점으로 갈 수 있는 최소비용의 정점을 선택.
   ( 이 정점은 선택된 정점그룹에 들어감 )
3. 이 정점에서 다른 정점으로 가는 비용과, 기존의 비용과 더 비교후에 더 작은 비용이 있으면 갱신.
4. 2-3번 과정을 V(정점수)-1 번 반복