9020: 골드바흐의 추측

import sys

def is_prime(n):
    if n == 1:
        return False
    for j in range(2, int(n**0.5) + 1):
        if n % j == 0:
            return False
    return True


for _ in range(int(sys.stdin.readline())):
    num = int(sys.stdin.readline())

    a = b = num//2
    while a > 0:
        if is_prime(a) and is_prime(b):
            print(a, b)
            break
        else:
            a -= 1
            b += 1

이전 문제인 '소수찾기(1978)'의 응용 문제지만 많은 어려움을 겪었다.
주의할 점은 반복문을 과도하게 사용하여 모든 경우의 수를 비교하고자 하면 시간초과가 난다는 점이였다.
두 소수의 차가 가장 작은 것을 출력해야 하기 때문에, 값을 2로 나누고 가운데 값으로 부터 +1, -1씩 하며 소수를 출력한다.

에라토스테네스의 체

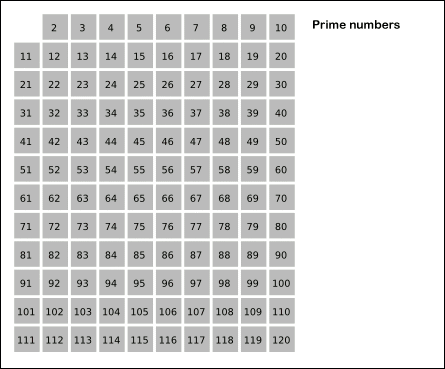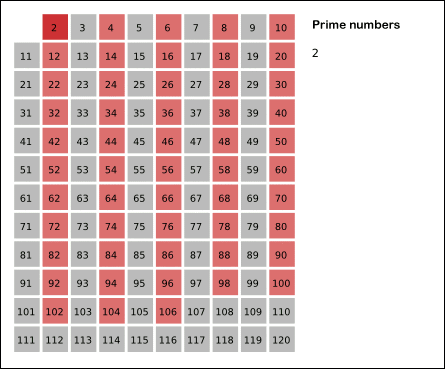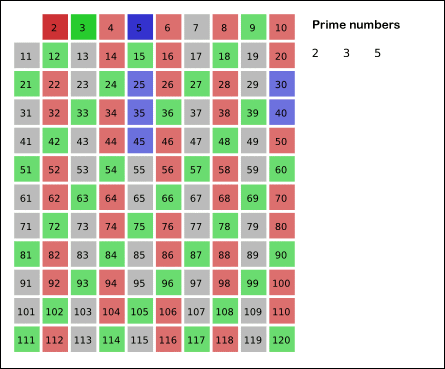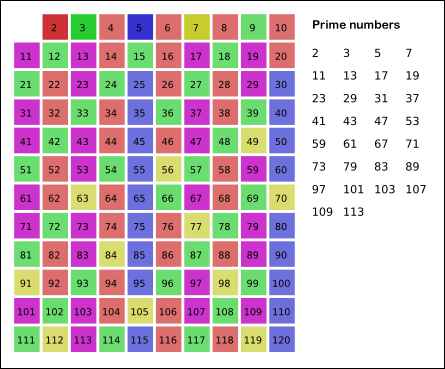
n보다 작은 가장 작은 수 i의 배수들을 False로 바꿔주면서 n까지의 소수들을 판정하는 방법으로 소수 관련 문제에서 굉장히 유용하게 사용할 수 있다.

def prime_list(n):
    # 에라토스테네스의 체 초기화: n개 요소에 True 설정(소수로 간주)
    sieve = [True] * n

    m = int(n ** 0.5)
    for i in range(2, m + 1):
        if sieve[i] == True:           # i가 소수인 경우 
            for j in range(i+i, n, i): # i이후 i의 배수들을 False 판정
                sieve[j] = False

    # 소수 목록 산출
    return [i for i in range(2, n) if sieve[i] == True]

출처 : https://this-programmer.tistory.com/409