주제는 : 10개 도시를 최단거리로 여행하는 법이며
- 현실세계에서 실제로 발생하는 많은 문제나 그런 문제들의 근본이 되는 문제를 해결하려면 지수 알고리즘이 필요하며, 이러한 문제는 다항 알고리즘으로는 풀 수 없다고 합니다.
- 다항을 의미하는 P, NP는 비결정적 다항을 의미하는데, 다항으로 풀지 못하는건 NP : 해결책은 빨리 찾을 수 없지만 , 해결책을 알고 있다면 빨리 입증을 할 수 있는 것들입니다
즉 'P'는 컴퓨터가 쉽게 해결할 수 있는 문제를 말하고, 'NP'는 직소 퍼즐이나 스도쿠처럼 한번 해결하면 검산하기 쉬운 문제를 뜻합니다.
중요한 부분은, 많은 NP 문제들은 사회가 직면한 가장 고질적이고 긴급한 문제에 해당한다.
-
예시 : 여행하는 외판원 문제 :
책에서는 직관적으로 와닿는 '최근접 이웃' 휴리스틱으로 찾은 해법이 표시되어 있다. 즉, 한 도시에서 시작해서 매번 아직 방문하지 않은 도시 중 가장 가까운 도시로 이동하는 방식이다. 시작하는 도시가 바뀌면 여행 경로가 바뀔 수 있다는 점에 주의해야 한다. 여기서 휴리스틱(heuristics)은 발견법이라고도 하며, 문제 해결 시 시간이나 정보가 불충분해 꼭 합리적인 해법을 찾을 수 없을 때, 또는 굳이 가장 이상적인 해법을 찾을 수 없을때, 또는 굳이 가장 이상적인 해답을 쓸 필요가 없을 때 현실적으로 정답에 가까운 해결책을 찾기위해 설계된 기법이라고 한다.
이 문제는 1800년대부터 지금까지 연구가 되어 오고 있으며, 이제는 더 큰 규모의 문제도 능숙하게 해결할 수 있지만, 아직도 최단경로를 찾는 방법은
모든 가능한 경로를 시도해 보는 것밖에 없으며, 예전보다 좀 더 기발해졌을 뿐이라고 합니다. -
아래 사진을 보면, 가능한 모든 해법을 완전 탐색하는 것보다 더 효울적으로 풀 방법이 없다고 한다. 이는 즉 알고리즘을 연구하는 사람들에게 좌절감을 주었다고 합니다.
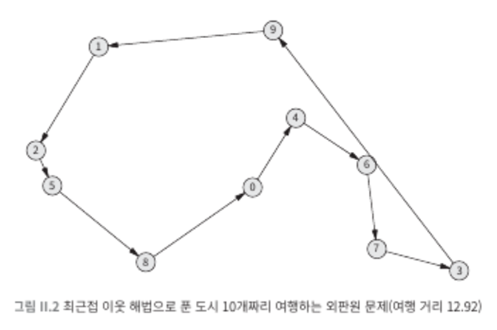
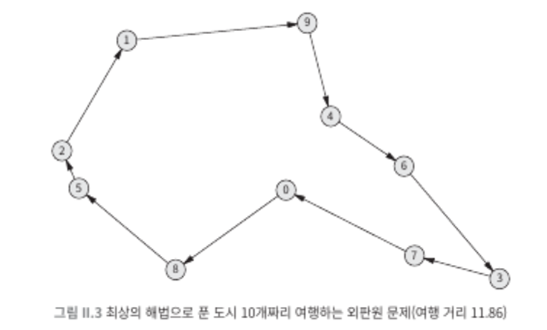
그중 스티븐 쿡 대학교수는 이런 문제 중 다수가 서로 동등하는 것을 증명해였고, 만일 우리가 그 문제 중 어느 한 문제를 해결하는 다항 시간 알고리즘(N제곱승 등)을 찾을 수 있다면, 이 모든 문제에 대한 다항 시간 알고리즘을 찾아 낼 수 있다는 것이다.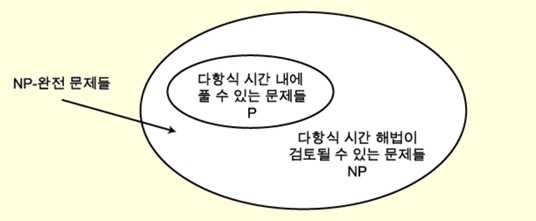
P=NP 문제가 중요하기는 하지만 현실적인 사안이라기보다는 이론적인 주제이며, 컴퓨터 과학자가 말하는 복잡도란 대부분 최악의 경우에 대한 것이지만, 보통은 최악의 경우까지 가지 않는다고 한다, 실제 상황에서는 대부분 근사치만 구하는 것으로도 충분하다.
참고 책 : '1일 1로그 100일 완성 IT 지식
