Big O Notation에 대하여...
알고리즘에서 Big O Notation이 무엇일까?
일단, 알고리즘이란 문제를 해결하는 방법이라고 할 수 있다.
만약, 어떤 문제를 두 가지 방법으로 원하는 결론을 얻어내었다면 둘 다 맞는 방법이라고 할 수 있다.
하지만 동시에 문제에 접근하는 방식이 서로 다르다면 둘 중에 어떤 코드가 더 나은 코드인지 생각해 볼 수도 있다.
예를 들어 문자열을 거꾸로 출력하는 코드를 작성해야 할 때,
문자열을 거꾸로 출력하는 다양한 방법에서 보이듯이 정말 여러가지 방법이 있다.
변수 이름, 함수 이름 등이 다른 것이 아니라 문제를 접근하는 방식 자체가 다르다는 것이다.
예를 들어 하나는 반복문을 사용했고 다른 하나는 리스트나 문자열을 이용한다고 했을 때,
어느 방법이 더 좋은 문제 해결 방법이라고 할 수 있을까?
이때, 사용되는 개념이 Big O Notation이다.
Big O Notation이란, 여러 코드를 서로 비교하고 성능을 평가하는 방법이라고 할 수 있다.
또한 Big O Notaion을 사용하면 코드를 그저 더 좋은 코드, 그저 그런 코드, 나쁜 코드라고 평가하는 것이 아니라
숫자로 코드의 성능을 나타낼 수 있다.
어쨌든 코드만 잘 돌아가면 되는 거 아닌가?
반복문을 쓰던, reverse, join을 쓰던 어쨌든 문자열을 거꾸로 출력하기만 되는 것 아닌가...?
기껏해야 연습용 코드에서 "hello world"나 쓰는 지금의 나 같은 사람들에게는
일단, 결과를 출력하는 것이 중요하지 코드의 효율성을 따져보는 것은 그다지 큰 관심사가 아니다.
당장 나의 경우도 "처음 문자열을 뒤집어서 출력해라"라는 문제를 보고선 성능은 신경쓰지도 않고
반복문을 거꾸로 돌면서 출력하면 되는 게 아닐까라는 생각을 했었고 다른 방법에 대해선 굳이 생각해 보지도 않은 것 같다.
그런데 수 천, 수 만개의 데이터를 다루는 상황에서 과연 이 방법이 최선이라고 할 수 있을까?
만약, 여러 방법 중 하나의 방법의 실행 속도가 다른 방법들 보다 몇 시간 더 빠르다면 이것은 분명히
성능적으로 어떤 코드를 선택해야 할지 고려해 볼 만한 상황이다.
위처럼 어떤 상황에서 문제를 해결하는 데 더 좋은 코드는 존재한다.
그리고 더 좋은 코드를 평가하기 위해 Big O Notation이 사용된다.
무조건 좋은 코드 ?
사실, 어떤 상황에서 A 코드가 B 코드보다 더 좋다고 해서 A 코드가 무조건 좋은 코드이고 B 코드가 좋지 않은 코드라는 것을 말하지는 않는다.
특정한 데이터의 범위에 따라 A 코드가 B 코드보다 더 좋은 코드일 수도 있지만,
B의 코드는 데이터의 범위에 상관없이 처리하는 속도의 변화가 크지 않다면 특정 상황에서
누군가에게는 B의 코드가 A 코드 보다 더 좋은 코드일 수도 있다는 것이다.
즉 꼭 어떤 코드가 무조건 최선의 코드일 수는 없다. 상황에 따라 다른 것뿐...
예를 들어 일반적으로 선택 정렬 알고리즘이 버블 정렬 알고리즘보다 효율적이지만,
거의 정렬된 배열이 입력이 주어졌을 때에는 버블 정렬이 선택 정렬보다 효율적인 것 처럼...
더 나은 코드??
더 나은 코드란 무엇일까?
- 빠른 속도
- 더 적은 메모리의 사용량?
- 더 짧은 코드?
- ...
더 나은 코드를 생각해볼 때 위 모든 조건들은 고려해볼만 하다.
가장 중요한건 어떤 상황이냐에 따라 다르다는 것이지만,
특히 알고리즘에서는 빠른 속도를 보이는 코드를 좋은 코드라고 보는 경향이 많은 것 같다.
다시 강조하자면, 가장 중요한건 상황에 따라 다르다는 것이다.
그렇다면, 보통 코드의 실행 속도는 어떻게 측정할까?
코드의 실행 속도를 측정하는 방법과 한계
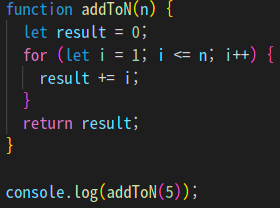
코드의 실행 속도를 측정하기 위해 1에서 N까지의 숫자를 더하는 두 개의 함수를 작성했다.
첫 번째 함수는 당장 떠올리기 쉬운 방법으로 결과를 담을 변수 result를 선언하고 0으
로 할당하여 1부터 N까지 반복문을 돌며 result에 N을 더해주는 함수이다.
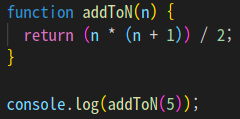
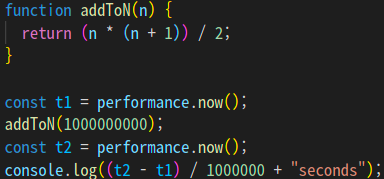
두 번째 함수는 위보다는 조금 더 생각해야 하는 방법이지만 코드는 훨씬 짧다.
코드가 짧다고 해서 더 좋은 코드라고 하기엔 어렵지만 첫 번째 함수와 다르게 반복문이 사용되지 않았고, 수학 공식을 이용한 함수이다.
두 함수는 서로 다른 방식으로 1부터 N까지를 더한 결과를 반환하도록 구현되었다.
이때, 두 코드의 실행속도를 측정하기 위해 performance.now() 메소드를 를 이용했다.
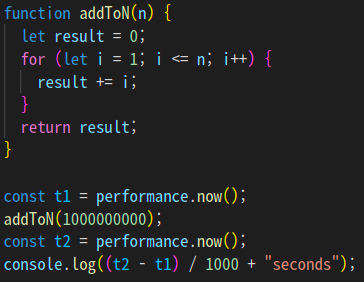
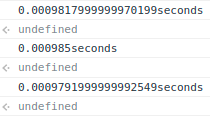
위의 사진 처럼 첫 번째 함수를 3번 실행했지만, 걸리는 시간은 모두 조금씩 다르다.
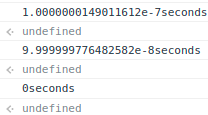
위의 사진처럼 두 번째 함수는 첫 번째 함수에 비해 실행 시간이 훨씬 짧찌만 이번에도 모두 걸리는 시간이 조금씩은 다르게 측정되었다.
결과적으로 실행 속도만 본다면 두 번째 함수가 더 효율적인 코드라고 볼 수도 있다.
하지만, 이렇게 수동적으로 코드가 실행되는 데 걸리는 시간을 구하고 이를 비교하는 것이
코드의 성능을 평가하는 데 효과적인 방법이라고는 할 수 없다.
왜냐하면 위에서 보았듯이 똑같은 코드라고 해도 다른 시간이 측정되기 때문이다.
또한 여러 이유가 있다...
- 기기에 따라 다른 실행 속도
- 백그라운드에 다른 프로그램이 돌아가고 있는지?
- performance.now()로 측정되지 못할 만큼의 빠른 코드라 하던지?
- 만약, 30시간이 걸리는 프로그램과 15시간이 걸리는 프로그램을 비교해야 했다면, 어떻게 해야 하는지...?
즉 단순히 코드의 실행 시간만을 가지고 더 효율적인 코드를 판별하기에는 부족하다.
그렇다면 더 효율적인 코드를 어떻게 평가해야 할까?
연산 횟수를 세자!!!
연산 횟수는 상황에따라 변하지 않는다.
어떤 코드에서 사용되고 있는 연산의 횟수가 5번이라면 이 코드는 어느 상황에서도 5번 연산을 해야 하는 코드이고, 10번이라면 어느 상황에서도 10번 연산을 수행하는 코드이다.

위의 코드는 N이 1이든 10억이든, 작든 크든 상관없이 연산을 3번 수행한다 (곱셈, 덧셈, 나눗셈)

위 코드에서 total += i라는 코드는 +와 =(할당)이라는 연산이 두 번만 행해지고
있다고 볼 수도 있지만 사실 이 코드는 반복문 안에 존재하고 있으므로 N의 크기만큼 이
연산 횟수도 늘어난다. (N이 5라면 위의 연산들을 5번 하는 것이다.)
이 코드에 대해 정확하게 연산 횟수를 세어 보자면 5n + 2라고 할 수 있지만,
하지만, 이렇게 정확한 숫자를 이용해 연산 횟수를 세는 것은 중요하지 않다.
5n+2이든지, 5n이든지, 50n이든지 중요한 것은 큰 그림을 보는 것이다.
두 번째 코드의 연산 횟수를 더 정확하게 표현한다면 아래처럼 표현해야 한다.
n이 커질수록 연산 횟수도 비례적으로 증가한다.