자료구조와 알고리즘 ?
자료구조는 데이터의 표현 및 저장 방법을 뜻한다.
알고리즘은 이렇게 저장된 데이터를 가지고(데이터를 대상으로) 문제를 해결하는 방법을 말한다.
let arr = [1,2,3,4,5];
위의 배열 선언은 자료구조적 측면의 코드이다.
let sum = 0;
for(let i of arr){
sum += i;
}위의 반복문 코드는 알고리즘적 측면의 코드이다.
이렇듯 자료구조와 알고리즘은 밀접한 관계를 갖는다.
자료구조가 결정되어야 그에 따른 효율적인 알고리즘을 결정할 수 있기 때문이다.
즉 자료구조는 데이터를 '저장'할 때, 알고리즘은 데이터를 '연산'할 때, 어떻게 하면 컴퓨터가 처리하기 쉽게 만드는지를 다루는 것이다.
만약, 값이 저장된 자료구조가 배열이 아니었다면 위의 반복문처럼 인덱스를 통해 순차적인 접근이 가능했을까??
배열이 아니었다면, 방법은 달라졌을 것이다.
1.상자가 쌓여있고, 이 상자안에 있는 책을 찾는다고 해보자.
여기서 쌓여있는 상자는 자료구조라고 할 수 있다. 그렇다면 이 자료구조에 담겨있는 데이터(책)을 찾기 위해 어떤 과정을 거쳐야 할까?
-> 위에 있는 상자부터 차례로 열어보며 찾아가야 한다.
2.상자가 일렬로 놓여있고, 이 상자안에 있는 책을 찾는다고 해보자.
또한 일렬로 놓여있는 상자도 자료구조라고 할 수 있다. 그렇다면 이 자료구조에 담겨있는 데이터(책)을 찾기 위해 어떤 과정을 거쳐야 할까?
-> 굳이 앞에 있는 상자부터 찾을 필요가 없다.
이렇듯 자료구조에 따라 알고리즘은 완전히 달라진다.
따라서 알고리즘은 자료구조에 의존적이라고 할 수 있다.
어떤게 더 쉬울까? - 99찾기
case 1
[
65, 21, 31, 28, 82, 60, 34, 29, 43, 79, 66, 29,
18, 74, 71, 93, 85, 31, 99, 46, 46, 73, 75, 8,
74, 10, 67, 51, 98, 50, 48, 26, 89, 92, 96, 20,
50, 94, 52, 61, 34, 70, 77, 46, 63, 58, 42, 86,
21, 22, 48, 71, 70, 19, 27, 9, 96, 70, 79, 89,
89, 54, 69, 16, 6, 35, 89, 72, 83, 13, 55, 28,
2, 17, 29, 25, 60, 55, 86, 30, 84, 68, 14, 29,
75, 45, 4, 63, 55, 39, 99, 45, 88, 28, 28, 1,
63, 24, 62, 51
]
case 2
[
0, 1, 2, 4, 5, 6, 6, 9, 10, 11, 12, 13,
17, 18, 19, 20, 26, 26, 27, 28, 29, 30, 32, 32,
32, 34, 34, 38, 40, 40, 42, 43, 46, 47, 47, 48,
50, 52, 54, 54, 55, 56, 56, 56, 57, 60, 60, 63,
64, 64, 64, 66, 66, 67, 68, 68, 69, 69, 69, 70,
71, 72, 72, 73, 73, 74, 76, 76, 78, 78, 79, 79,
79, 80, 83, 84, 85, 85, 85, 85, 86, 89, 90, 90,
90, 91, 91, 92, 92, 92, 93, 93, 94, 95, 96, 96,
98, 98, 99, 99
]
알고리즘의 성능분석
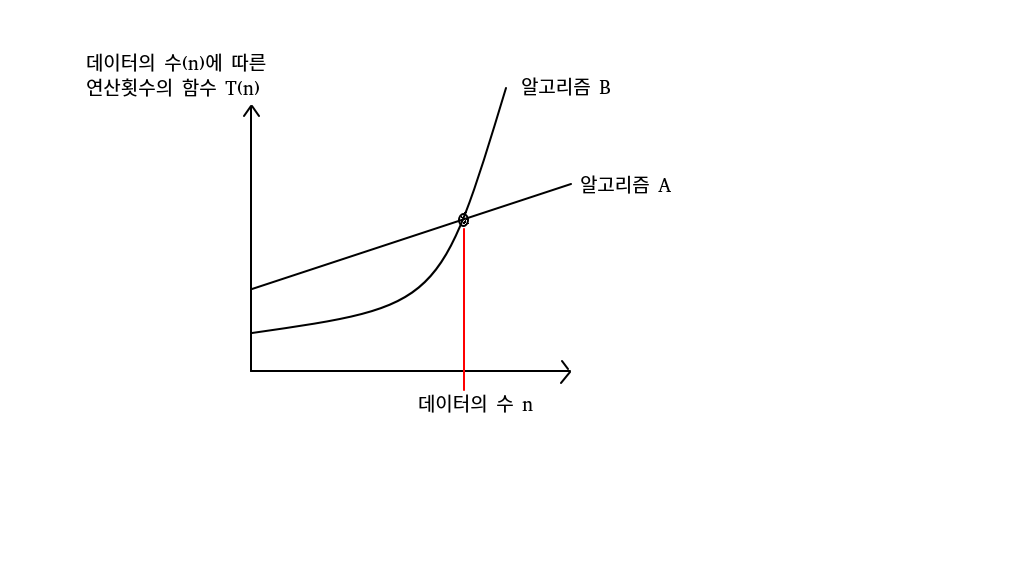
알고리즘 별 연산횟수 함수 T(n)을 구하면 위의 그림에서 보이는 바와 같이 그래프를 통해 데이터 수의 변화에 따른 연산횟수의 변화 정도를 한 눈에 파악할 수 있다.
동일한 기능을 제공하는 서로 다른 두 알고리즘이라 했을 때, 위 그림을 통해 알고리즘의 성능을 비교해 본다면, 아래와 같은 결과를 얻을 수 있다.
1.데이터의 수가 적으면 알고리즘 B가 더 빠르다.
2.근데 데이터의 수가 많아지면 알고리즘 A가 더 빨라진다.
그렇다면 아래와 같은 결론이 맞을까?
데이터의 수가 적은 경우에는 알고리즘 B를 적용하고, 데이터의 수가 많은 경우에는 알고리즘 A를 적용해야 한다.
맞긴하다.
그런데 데이터의 수가 적은 경우, 속도 차이가 난다면 얼마나 날까?
알고리즘 성능에서 중요한 부분은 데이터의 수가 많아짐에 따른 연산횟수의 증가정도이다.
그렇다면, 알고리즘 A가 더 좋은 알고리즘이라고 할 수 있을까? 그렇다.
그럼 B 알고리즘은 쓸모가 없는 것일까? 아니다.
그렇다면 대체 정답이 무엇일까?
상황에 맞게 알고리즘을 사용해야 한다.
대게 A와 같이 안정적인 성능을 보장하는 알고리즘은 B와 같은 알고리즘에 비해 구현의 난이도가 높은 편이다. 따라서 데이터의 수가 많지 않고 성능에 덜 민감한 경우라면 구현의 편의를 이유로 B 알고리즘을 선택할 수도 있는 것이다.
즉 적절한 상황에 맞게 판단해서 알고리즘을 구현 및 사용할 줄 알아야 한다.
추상적 자료형 (ADT : Abstract Data Type)
이름처럼 추상적인 개념이다.
자료가 어떤 형태로 저장되며 자료의 삽입/삭제/탐색 등 필요한 작업(기능, 연산)은 어떠한 것이 있는지 정의만 하고, 이 기능들이 구체적으로 어떻게 구현되어야 하는지는 명시하지 않는다.
이러한 추상적 자료형에는 스택, 큐, 리스트, 트리 등이 있다.
이 중에서 스택이라는 자료형을 예를들자면,
스택은 아래와 같은 속성을 갖는다.
1.후입선출(LIFO)의 특징
2.기능
- 삽입 push()
- 삭제 pop()
- 스택의 마지막에 삽입된 데이터를 조회하는 peek()
- 크기를 확인하는 size()
- 스택이 비었는지 확인하는 isEmpty()
그리고 이러한 스택이 내부적으로는 배열로 구현되는지, 연결 리스트로 구현되는지 또는 size 연산을 수행할 때 원소의 개수를 일일이 세는지 아니면 개수를 따로 저장해 두는지와 같은 세부 사항들은 추상 자료형에서는 다루지 않으며, 그걸 다루기 시작하면 자료구조의 영역으로 넘어가게 된다.
이렇듯 '스택'이라는 자료형이 어떤 식으로 자료를 저장하고 꺼내며, 어떠한 기능이 있는지만 정의하는 것. 여기까지가 추상적 자료형으로써 스택의 개념이다.
추상적 자료형 vs 자료구조
둘은 명백히 구분되지만, 추상 자료형과 그것을 구현한 자료구조의 이름이 비슷하거나 아예 같은 경우가 많다.
이를 구분하는 법은 조금이라도 구현 방법이 정해져 있는지 보는 것이다.
즉 추상적 자료형을 구체화 시킨 것이 바로 자료 구조이다.
스택이나 큐는 구현 방법이 전혀 정의되어 있지 않으니 추상 자료형이고, 배열은 '연속적'으로 저장되어 있도록 구현되어 있어야 하므로 자료구조이며, 연결 리스트도 다음 '데이터의 위치를 저장'하는 방식으로 정해져 있으니 자료구조이다.
| 개념 | 정의 | 예 |
|---|---|---|
| 추상적 자료형 | 자료의 형태 및 연산을 정의만 한 것 | 리스트, 스택, 큐, 트리 등 |
| 자료구조 | 추상적 자료형을 구체적으로 구현한 구현체 | 콜 스택, 연결 리스트, 배열 |
| 알고리즘 | 문제를 해결하는 방법, 절차 | 정렬, 탐색 |
