Vanishing Gradient

DNN 을 무턱대고 깊게 만들면 vanishing gradient 문제가 발생한다. Layer 이 많으면 입력 층에 가까울 수록 미분이 작아지기 때문이다. 만약 Activation 을 sigmoid를 사용했다고 가정할 때, 이 함수의 최대 기울기는 1/4 이기 때문에 3번만 반복해도 최대 1/64 가 된다.

Update 는 $\frac{\partial L}{\partial W}$ 만큼 될텐데, 이 값이 너무 작아지면 loss 가 줄어들지가 않음. 강의에서는 네트워크를 사원 -> 부장 -> 임원 에 비유하는데, 사원에서 망하면 위에서 손을 쓸 수 없다고 한다.

ReLU

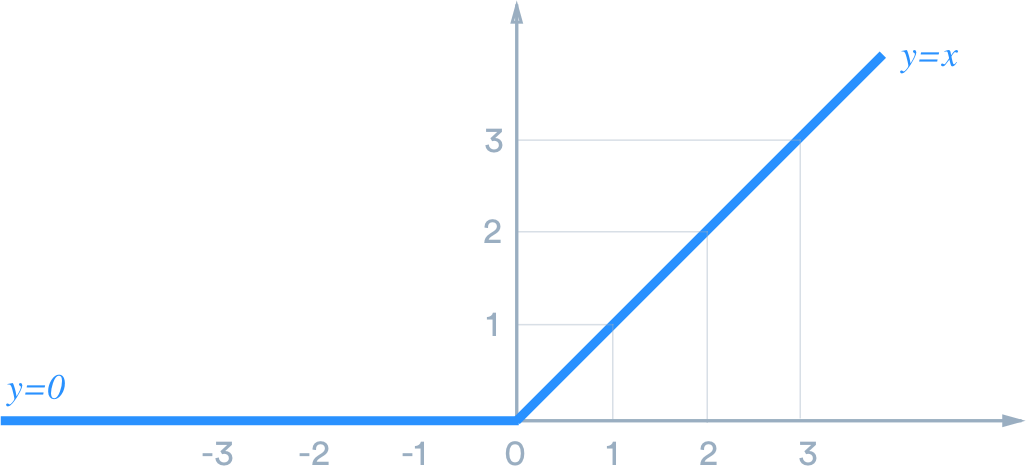
ReLU (Rectified Linear Unit) 을 사용했을 때, 양수값이 들어오면 미분값이 1이기 때문에 activation 으로 인해 vanishing gradient 문제가 생길일이 없다.

Vanishing Gradient 실습

Sigmoid 를 사용해서 층을 깊게 쌓았을 때, 앞에 있는 gradient 가 0에 수렴하는 것이 보임 (전혀 학습이 되고있지 않음). Underfitting 이 일어남.

하지만, ReLU 를 사용하니 gradient 가 conv1 까지 쭉쭉 전달이 됨. 단지 activation 만 바꾸었을 뿐인데도 학습이 잘 됨.

Batch Normalization

목적: 어떤 node 에 대해서 non-linearity 를 최대한 살리는 쪽으로 재배치를 시킴.

평균이 0이고 분산이 1으로 standard normalization 하면 안될까..?

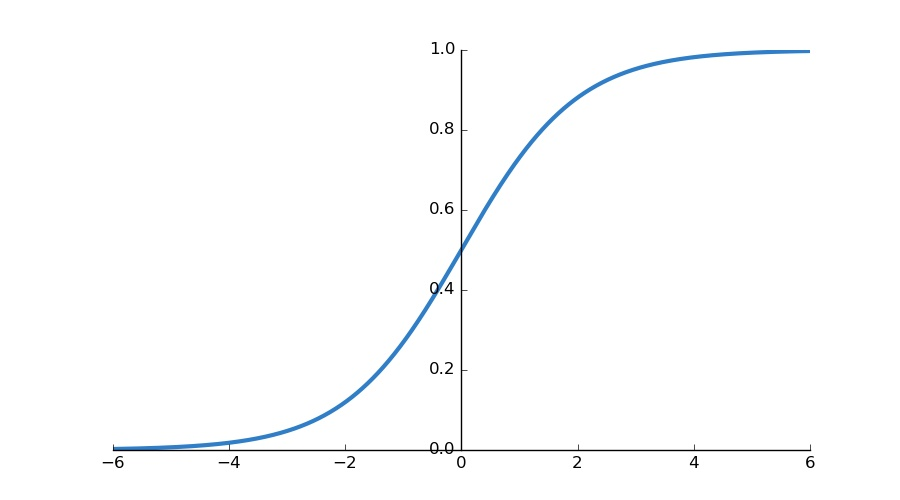
Sigmoid 는 0 주위에서 linear 하기 때문에 standard normalization 을 수행할 시 non-linearity 를 갖다 던지는 꼴이 됨..

의 정규화를 수행할 때 평균은 $b$, 분산은 $a^2$ 인 normalization 을 학습시킬 수 있음. 즉, node 당 2개의 learnable parameters 가 추가되는 거임.

Layer normalization 은 이 과정을 layer 단위로 수행하는 것 뿐임.

따라서, vanishing gradient 문제를 어떻게 해결해야할 지 물어본다면 ReLU / normalization 방법을 이야기 하면 됨.

Batch Normalization 실험

이미 ReLU 로 vanishing gradient 를 해결 해서 BN 을 추가해도 별 차이가 없었다..

하지만 Sigmoid 에서는 11% -> 94.4% 까지 올라감! histogram 을 보았을 때 마지막 층에서 값이 -5로 수렴해버림 (미분을 따라간듯). 문제는, 한쪽 끝값으로 가면 미분값이 0이기 때문에 vanishing gradient 문제가 생김. Batch norm 은 이 왼쪽으로 가려는 걸 끌고 와서 vanishing gradient 를 해결함.