다음 글은 책 [알고리즘으로 배우는 치트시트]와 샌디에고 주립대학 Edwards 교수님의 강의를 참고하여 포스팅하였습니다.
1. 알고리즘 학습과 문제해결 아이디어
알고리즘은 단순히 말하자면 문제의 유형을 파악하여 아이디어와 해법을 도출해내는 것이 핵심이라고 할 수 있다. 그러기 위해서는 다음과 같은 3가지를 알아야 한다.
- 데이터 구조와 저장 방식
- 데이터 구조의 기본 조작
- 알고리즘 문제 해결 가이드
이제 차근차근 각 항목에 대해 Deep Dive해보도록 한다.
1.1 데이터 구조와 저장방식
핵심은 다음과 같다.
문제 분석시, 데이터의 기본 저장방식인 하부구조 에서 상부구조 , 즉, 구체적인 방식으로 사고하는 것이 핵심.
하부구조란, 데이터의 기본 저장 방식으로,
- 배열
- 연결리스트
가 있다.
아래는 상부구조에 속하는 것들이며, 우리가 흔히 아는 자료구조라고 할 수 있다.
- 해시테이블
- 스택
- 힙
- 트리
- 그래프
즉, 배열과 연결리스트를 통해 위와 같은 상부구조(해시테이블, 스택, 힙등)을 절차적으로 구현할 수 있는 것이다.
예를 들어 큐(Queue), 스택(Stack)은 배열의 확장 축소 문제를 다루고, 연결리스트의 메모리 공간 문제를 다룬다. 모두 두가지 하부구조로 구현이 가능하다.
1.1.1 데이터 저장 방식의 장단점
다만, 배열과 연결리스트의 장단점이 있다.
| 장점 | 단점 | |
|---|---|---|
배열 | 1. 연속된 저장 방식을 사용하므로 임의로 접근이 가능 2. 인덱스를 통한 빠른 접근 3. 저장 공간을 절약 | 1. 연속되는 저장방식으로 인해, 메모리 공간을 한 번에 할당해야함. 2. 배열 확장시 시간 복잡도는 O(N) |
| 연결리스트 | 1. 다음의 위치를 가르키는 포인터에 의존하기 때문에 배열의 확장과 같은 문제는 발생하지 않는다. 2. 요소의 선,후행요소만 알면 조작해 제거, 삽입이 수월하고 시간복잡도가 O(1) | 1. 저장 공간이 연속되지 않아 임의 접근이 불가능하다. 2. 각 요소에 반드시 선/후행의의 위치에 대한 포인터를 저장해야 함 >> 많은 메모리 소모 |
1.2 데이터 구조의 기본 조작
모든 데이터구조에서 기본작업은 순회(trzversal) 와 접근이며, 보다 구체적으로는 추가, 삭제, 검색, 수정이다.
그리고 각 데이터 구조에 대한 순회와 엑세스는 선형, 비선형 방식이 있고 아래가 각 방식에 대한 대표적인 예이다.
- 선형: for/while 반복
- 비선형: 재귀
1.2.1 배열
배열 순회는 전형적인 선형 반복 구조이다.
//배열의 기본조작, 순회는 선형방식(for문)!
void traverse(in[] arr){
for(int i=0;i<arr.length;i++){
//반복 엑세스 arr[i]
}
}1.2.2 연결리스트
연결리스트의 핵심은 노드 이며 이를 정의하는 클래스 코드는 다음과 같다.
public class LinkedList<E> implements ListI<E>{
/* ************************************************** */
//Inner class (Type Node<E>), Nothing else can access!!
class Node<E>{
E data; //Type E
Node<E> next;
//Constructor
public Node(E obj){ //(E obj) 항상 어떠한 객체를 받게됨
data = obj;
next = null; // initialization next pointer
}
}
/* ************************************************** */
private Node<E> head;
private int currentSize;
// makes time complexity O(1) when each node in LinkedList increases the size by 1
//constructor
public LinkedList(){
head = null;
currentsize = 0;
}
.....
}아래 그림은 해당 코드(연결리스트에서의 노드)를 연결리스트화해서 시각화 한 것이다.
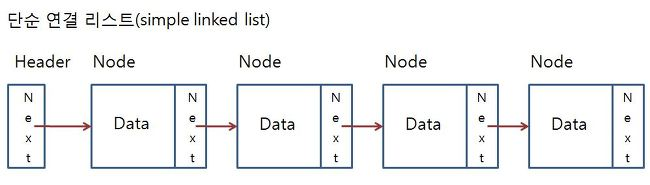
연결리스트는 순회와 반복 및 재귀구조를 갖는다.
class ListNode{
int val;
ListNode next;
}
void traverse(ListNode head){
for(ListNode p = head; p!=null; p=p.next){
//p.val반복
}
}
void traverse(ListNode head){
//전위 순회 head.val
traverse(head.next);// 다음노드를 가리키는 포인터를 파라미터에 넣고 재귀 돌리기!
//후위 순회 head.val
}갑자기 전위, 후위 순회가 튀어나왔다.
핵심은 프레임 사고이다.
이를 연마하기 위해서는 이진 트리가 제 격이므로 잠깐 다루고자 한다.
연결리스트의 전위, 후위 순회가 있듯, 이진 트리에서도 전위, 중위, 후위순회가 있다. 예를 들어 head.val을 프린트하면 순서대로 프린트하며, 후위 순회는 반대로 프린트한다.
이진트리에서의 전위 순회
- 순서: Root - Left - Right
class TreeNode{ int val; TreeNode left; TreeNode right; public TreeNode(int val){ this.val = val; this.left = null; this.right = null; } } void preOrderTraversal(TreeNode root){ if(root == null) return; System.out.println(root.val + " "); // visit root node preOrderTraversal(TreeNode left); //traverse left subtree preOrderTraversal(TreeNode right); //traverse right subtree }
중위 순회
- 순서: left - Root - Right
void inOrderTravseral(TreeNode root){
if(root==null)return;
inOrderTraversal(root.left);
System.out.println(root.val+ " ");
inOrderTraversal(root.right);
}후위 순회
- 순서: left - Right - Root
void postOrderTravseral(TreeNode root){
if(root==null)return;
postOrderTraversal(root.left);
postOrderTraversal(root.right);
System.out.println(root.val+ " ");
}햇갈리니 다음 그림을 잘 참고하자.
[reference : 전,중,후위순회의 이해를 돕는 그림]
현무님의 Naver Blog 이진트리-순회방법-swift 중...
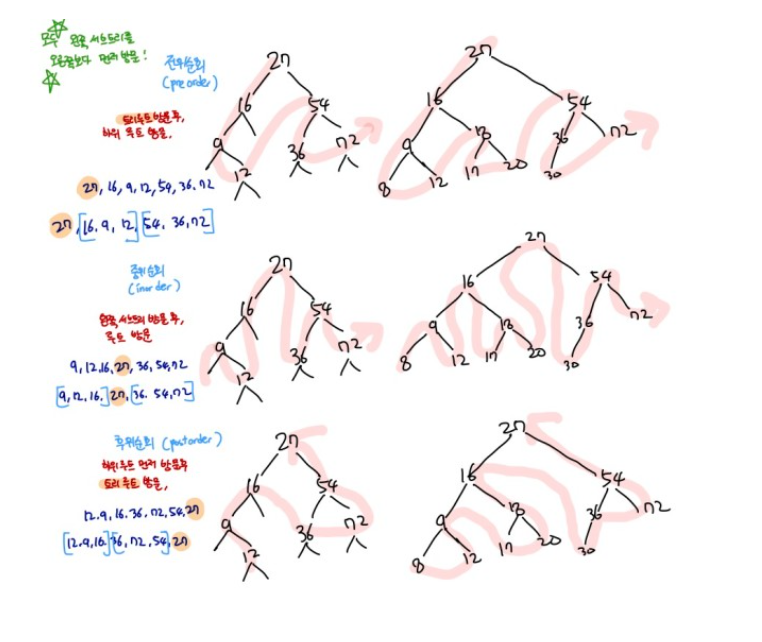
이진 트리 순회는 일반적인 비선형 재귀 순회 구조이다.
class TreeNode{
int val;
TreeNode left, right;
}
void traverse(TreeNode root){
//전위순회
traverse(TreeNode left);
//중위순회
traverse(TreeNode right);
//후위순회
}이진트리 순회는 N항 트리 순회로 확장이 가능하다.
class TreeNode{
int val;
TreeNode[] children;
]
void traverse(TreeNode root){
for(TreeNode child: root.children)
traverse(child);
}
다시한 번 강조하지만, 핵심은 프레임 사고이다. 추가, 삭제, 수정,검색에 상관없이 프레임을 참고하고 프레임 구조를 기반으로 구체적인 문제에 코드를 추가하면 된다.
다음 포스팅에서 데이터 구조의 특성과 단점에 대한 이해를 통해 알고리즘을 학습한다.
좀 더 고민하기
배열의 저장곤간을 효율적으로 사용하여 저장할 수 있는 장점이 연결리스트와 비교할 수 있는 것인가?
포스팅을 하며 느낀점
기본적으로 알고 있고 익숙한 용어라고 해도 이 책의 저자의 설명하는 방식이 독측하여 이해하는데 시간이 꽤 걸렸다. 2 회독을하며 또 새로운 것 같다. 역시 학습은 반복학습이 중요함을 체감한다...
또 책에서 함축하고 있는 내용이 있어 (독자가 다 알거라 하지만 나는 잘 이해 못함...ㅜ) 추가 설명을 위해 글이 너무 길어진 느낌이다...
