20강 - 다항분포 및 코시분포

MostlyFor·2023년 1월 9일
확률론
0

확률론

목록 보기
19/20

해당 내용은 아래 강좌를 정리한 내용입니다.
https://www.edwith.org/ai152

학습목표

다항분포의 결합분포, 주변분포 및 조건부분포를 구할 수 있으며, 코시분포의 확률밀도함수를 구할 수 있다.

핵심 키워드

  • 2차원 LOTUS(무의식적인 통계학자의 법칙)
  • 다항분포(Multinomial Distribution)
  • Lumping Property
  • 결합분포, 주변분포, 조건부분포
  • 코시분포(Cauchy Distribution)
  • 전확률정리(Law of Total Probability)

정규분포의 합

if X∼N(μ1,σ12),Y∼N(μ2,σ22) and indepThen X+Y∼N(μ1+μ2,σ12+σ22)if~ X \sim N(\mu_1,\sigma^2_1),Y \sim N(\mu_2,\sigma^2_2)~and~indep\\ Then ~X+Y \sim N(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2)

증명은 적률생성함수로 구할 수 있음.

Z∼N(0,1)=>M(t)=et2/2X∼N(μ1,σ12)=>M(t)=eZ\sim N(0,1) => M(t)=e^{t^2/2}\\ X \sim N(\mu_1,\sigma^2_1) =>M(t)=e

일반적인 X에 대해 배우지 않았으므로 일단 생략하고 결과를 알아두자.

정규분포 2개가 있을 때 두 정규분포의 합은 정규분포를 따른다!

EX) Z1과 Z2가 표준정규분포를 따를 때 E |Z1 - Z2| 를 구하라

→ X=Z1-Z2 라 하면 X ~ N(0,2)이다. 정규분포 정규화를 이용하면

E |Z1-Z2|=E |X| = E∣2Z∣E|\sqrt {2}Z|=2E∣Z∣=\sqrt 2 E|Z| = 이거 그냥 적분 하면 됨.

이제부터 다변량분포

다변량분포(Multinomial)란 한 개 이상의 확률변수가 포함된 결합분포함수

다항분포 (Multinomial), 다변량정규분포 2가지를 배움

다항분포 (Multinomial) : 이항분포의 연장선

X⃗\vec X ~ Mult(n,p⃗\vec p) : 여기서 p는 벡터를 의미함. p⃗=(p1,...,pk)\vec p=(p_1,...,p_k)

ㅎ확률벡터에서는 모든 항을 더하면 1이 되어야하며 음이 아닌 실수여야함.

n은 n개의 가짓수를 얘기함.

하나의 예시로는 n개의 물건을 k가지 종류 중 하나로 분류를 하는데 X는 k가지 종류가 각각 얼마나 되는지를 나타내는 것임.

다항분포를 구성하기 위해서는 오직 하나로 구분되어야함 2개거나 0개면 안됨.

이항분포가 실패와 성공만 다루었다면 다항분포는 k가지의 사건이 있는 것임.

PMF :

P(X1=n1,...,Xk=nk)=n!n1!..nk!p1n1...pknkP(X_1=n_1,...,X_k=n_k)=\frac{n!}{n_1!..n_k!}p_1^{n_1}...p_k^{n_k}

특이한 특징

  1. marginal distribution

원래라면 정의대로 결합확률분포에서 모두 더해야하지만 이 경우 각각의 물체 구별의 시행이 모두 독립임를 생각해보면 X_1이 n_1가지일 확률은 이항분포Bin(n,p_1)를 따른다고 할 수 있음.

  1. 조건부 분포 : 이미 어떠한 그룹이 정해졌을 경우

Cauchy distribution

Caushy Interview problem - 인터뷰에 자주 나온다고 함.

코시 분포는 X, Y i.i.d ~ N(0,1)일 때 X/Y임.

악랄하다고 소문난 분포

평균값이 없는 분포, 구하려고 하면 발산함.

CDF

T=XY,CDFP(XY≤t)=P(X∣Y∣≤t)=P(X≤∣Y∣t)=∫−∞∞∫−∞∣y∣tfX,Y(x,y)dxdy=12π∫−∞∞e−y2/2∫−∞∣y∣te−x2/2dxdyT=\frac{X}{Y},CDF\\ P(\frac{X}{Y}\le t)=P(\frac{X}{|Y|}\le t)=P(X\le|Y|t)\\ =\int_{-\infin}^\infin\int_{-\infin}^{|y|t} f_{X,Y}(x,y)dxdy\\ =\frac{1}{\sqrt{2\pi}}\int_{-\infin}^\infin e^{-y^2/2}\int_{-\infin}^{|y|t} e^{-x^2/2}dxdy

  1. Y에 절댓값을 취하는 Y ~ N(0,1) 에서 음수값을 가질 수 있기 때문. 정규분포의 대칭성 상 절댓값을 취한다고 해서 바뀌지 않음. X가 양수일 경우 Y의 부호변화에 관계없고 X가 음수일 경우도 Y의 부호와 관계없이 같은 값을 가짐. X가 부호를 최종적으로 결정하므로 Y의 부호는 관계가 없음.

  2. pdf로 확률을 구할 땐 P(S) S를 만족하는 부분에 대한 적분을 해주면 됨.

  3. 저기에서 우리가 적분을 할 수 없는 형태가 나오는데 우리는 대신 pdf를 구할 수 있음. 왜냐하면 pdf는 cdf를 적분한 식이기 때문임. 극한의 계산임.

  4. 이어서 나오는 내용은 다음과 같음

코시 분포의 pdf를 구하는 2번째 방법 - 전체 확률의 법칙

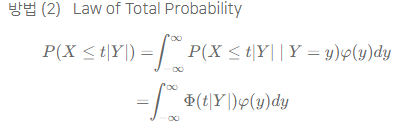
  1. X와 Y가 독립이기 때문에 Y에 y를 대입할 수 있음.
profile
MostlyFor
이전 포스트

19강 - 결합, 조건부, 주변 확률질량함수

다음 포스트

21강 - 공분산과 상관계수

0개의 댓글