문제

https://softeer.ai/practice/info.do?idx=1&eid=654

첫 시도

from sys import stdin
import itertools

n = stdin.readline().rstrip()
input_list = list(map(int, stdin.readline().rstrip().split()))

bus_combination = itertools.combinations(input_list, 3)
bus_combination = list(bus_combination)

count = 0
for i,j,k in bus_combination :
    if(i<j and i>k): count +=1

print(count)

문제에 거의 답을 거저 줬다. i<j, i>k 를 만족하는 조합의 개수를 찾으면 된다. 갯수만 알면 되기 때문에 굳이 i,j,k로 ai aj ak를 찾는 이런 과정은 스킵했다. (뒤의 설명에서도 i,j,k를 쓰니 혼동 주의)
심플하게 그냥 조합을 구해서 해당 식을 대입하면 바로 풀릴 줄 알았다.

그런데 ..

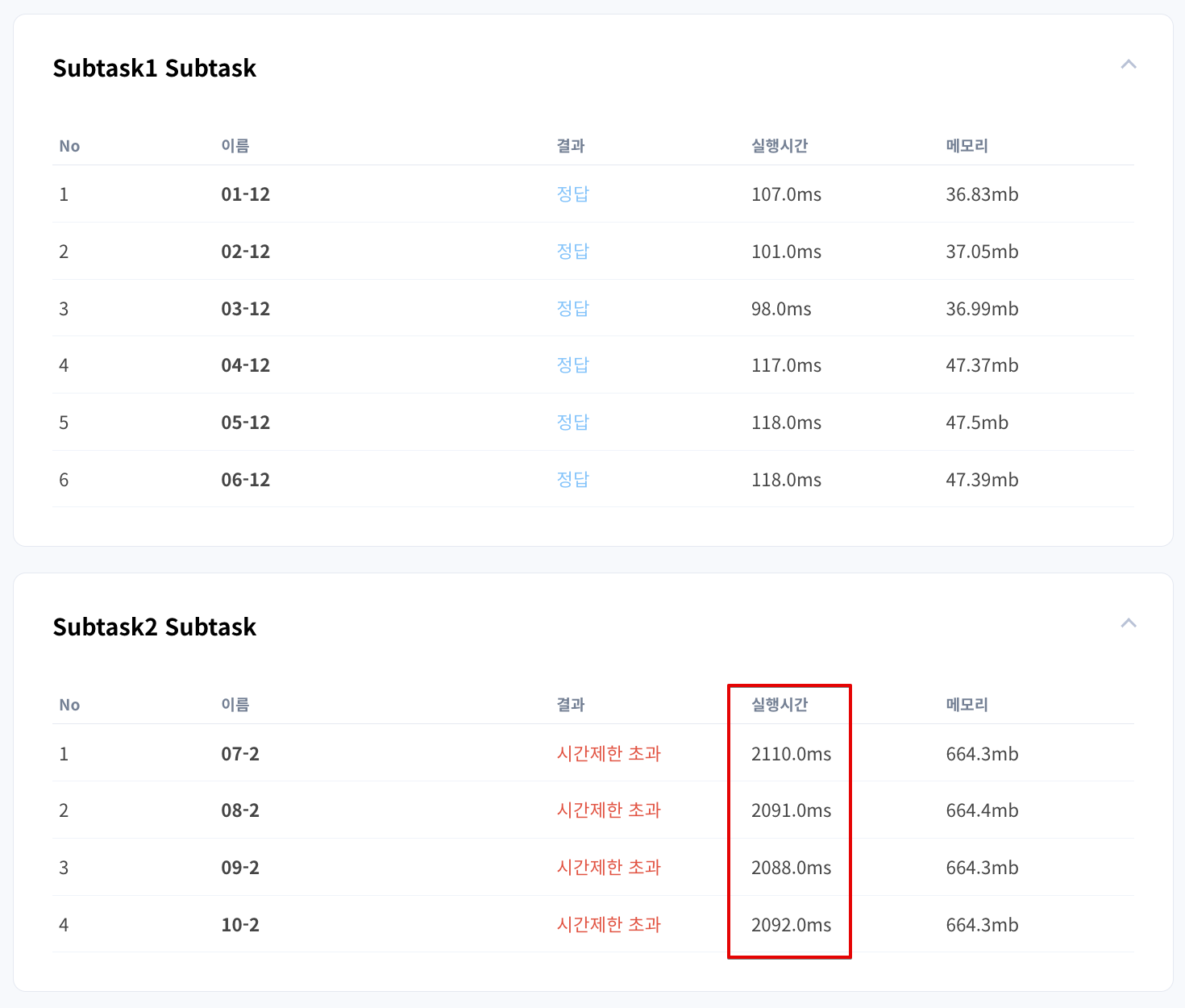
O(N^3) 구조를 쓰다보니 역시나 시간초과가 났다. 간당간당하게 제한시간 2초를 넘어서 어떻게든 조금이라도 for문을 덜 돌게 해보고자 노력했는데 헛수고였다.

두번째 시도

from sys import stdin

n = int(stdin.readline().rstrip())
input_list = list(map(int, stdin.readline().rstrip().split()))


count = 0
circle = 0

for i in range(n):
    circle = 0
    for j in range(i+1, n):
        if input_list[i] < input_list[j]:
            circle += 1
        elif input_list[i] > input_list[j]:
            count += circle

print(count)

기본 아이디어는 똑같다. i<j, i>k 를 만족하는 조합의 개수를 찾을 것이다.
그런데 이번에는 O(N^2)이다. 어떻게 된 일일까?

1차 시도에서 나는 입력받은 리스트 순서에 위배되지 않게 i,j,k를 정하고 i<j, i>k의 조건을 만족하면 카운트를 세서 답을 내고자 했다.

여기서 조합 이라는 점과 j와 k가 i를 기준으로 양분된다는 점에 주목해보자.

(1) 조합

입력예제4 를 가져왔다.
4 2 5 3 1
여기서 4를 기준으로 조합을 몇개 만들어 보겠다.
425 423 421
453 451
431

만들어진 조합의 특징을 보면, 기준점 4 이후에 오는 숫자가 배열의 바로 뒤의 숫자(2) 여도 되고, 그 보다 뒤에 있는 숫자(3)이어도 된다.
4 다음 오는 2를 2차 기준으로해서도 바로 다음 숫자인 5가 와도 되고, 1이 와도 된다.

다들 알고있는 조합의 특징이니 이정도만 설명하고 넘어가겠다.

(2) j와 k가 i를 기준으로 양분

i<j, i>k 의 뜻은 조합에서 두번째 숫자는 i보다 작아야하고, 세번째 숫자는 i보다 커야한다는 뜻이다.
i보다 큰 숫자를 O, 작은 숫자를 X 로 표현할 수 있다.

(1),(2)를 토대로 아래 그림을 그려봤다.

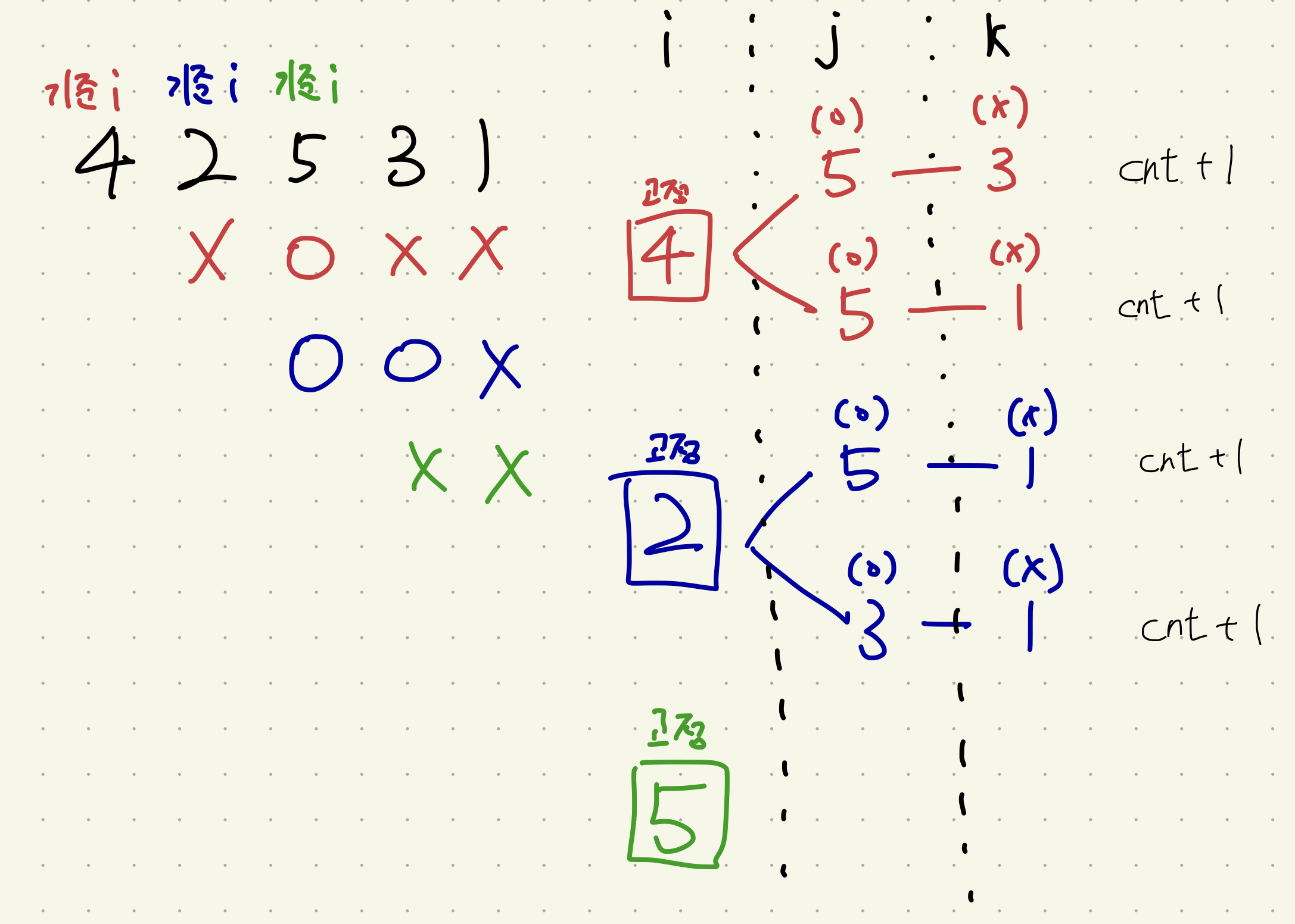
즉, i를 기준으로 뒤에오는 숫자의 조합이 i O X 이면 된다. 그 갯수를 세면 답이다.

이 논리는 기준점 i와, i 기준 그 뒤의 숫자들을 순회가며 O/X를 판단하는 구조이기 때문에 O(N^2)으로 구현할 수 있다.

기준점 i가 크게 돌고 그 안에서 기준점 다음 숫자를 찾느라고 작게 또 돈다. (구구단 구현법이다)

잠깐, 그럼 갯수는 어떻게 셀건가?
그림을 다시 보면 X가 나올때마다 그 앞에 O의 갯수를 세어서 합하면 된다는걸 알 수 있다. 수학적으로 증명은 못한다..
이 논리를 2중 for 문안에 넣었다.

짜란!@

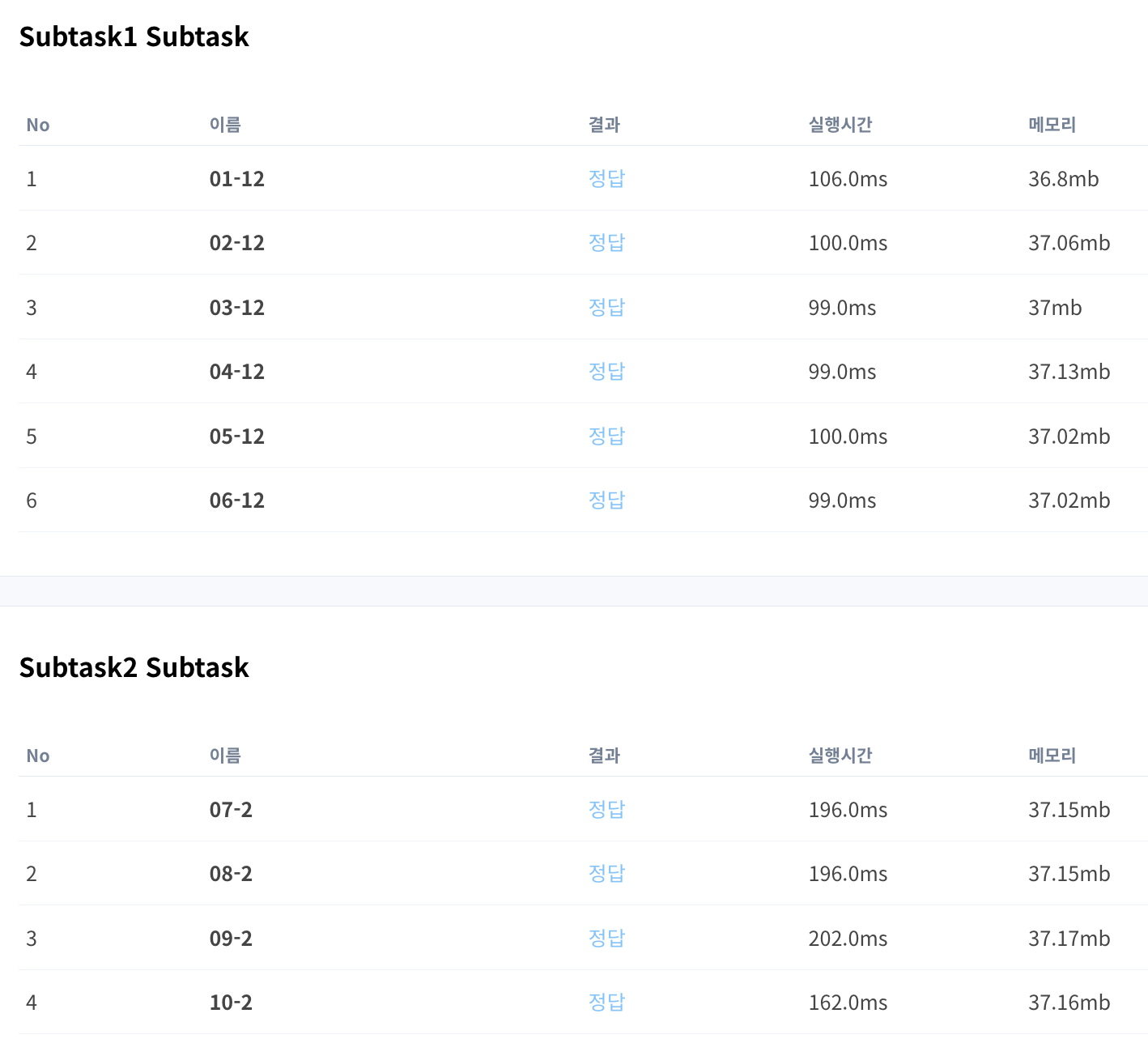
수학 연산으로 시간복잡도를 줄여버릴 수 있다는 것을 깨달은 아주 소중한 문제이다. 전혀 다른 구조로 접근하는 법을 알게 되었다.

---

말로는 잘 설명할 수 있을 것 같은데 글로 설명하려니 참 어려운 것같다.
이해 안되는 부분이 있거나 지적사항 있으시다면 아낌없는 댓글 부탁드립니다.

Shout out to Pabby