알고리즘이란?

알고리즘이란, 어떤 문제를 해결하기 위한 자세한 방법입니다.
라면을 끓이는데 있어 방법은 여러가지가 있을 수 있는데요, 여기서 모두 목적은 같은데 방법이 조금씩 다릅니다. 같은 문제를 해결하기 위해서도 다양한 알고리즘이 존재합니다.

좋은 알고리즘이란?

다양한 알고리즘 중에 좋은 알고리즘이란 두 가지 조건을 충족하는 알고리즘을 말합니다.

1. 문제를 해결하는 것
2. 문제를 더 잘 해결하는 것

컴퓨터 알고리즘이란?

컴퓨터가 어떤 문제를 해결하기 위해서 컴퓨터가 이해할 수 있는 방식으로 정리되어있는 해결 방법입니다.

예를 들어 컴퓨터가 자주 마주하는 "정렬"이라는 문제는 뒤죽박죽 섞여있는 숫자들을 순서대로 배치하는 것인데요.

[3, 4, 2, 5, 8, 17, 1] # 뒤죽박죽

[1, 2, 3, 4, 5, 8, 17] # 정렬

이 때 정확하고 효율적으로 숫자들을 정렬하는 알고리즘을 프로그래밍을 통해 찾아야 합니다. 따라서 프로그래밍과 알고리즘은 뗄 수 없는 관계라고 합니다.

하나의 문제, 여러 가지 알고리즘

도서관에 책이 알파벳 순으로 정리되어있는데, 어린왕자라는 책을 찾고 싶다면 어떻게 해야 할까요?

제일 왼쪽부터 시작해서 해당 책 이름이 있다면 책을 꺼내면 됩니다. 다른 방법은 어떤 것이 있을까요? 책이 알파벳 순으로 정리되어있다는 가정 하에, 가장 중간에 있는 단어를 기준으로 왼쪽에 있다면 중간을 기준으로 오른쪽에 있는 책들은 보지 않아도 됩니다. 이런 식으로 반씩 줄여간다면 어린왕자라는 책을 찾을 수 있습니다.

위의 예시는 탐색 문제입니다.

그리고 어떤 방법으로 푸느냐에 따라 걸리는 시간이 달라지는데, 다양한 방법들을 고민하고 분석하는게 알고리즘입니다.

탐색 알고리즘

탐색이란 저장된 정보들 중에서 원하는 값을 찾는 것을 말합니다.

예를 들어 파이썬 리스트에서 숫자를 찾는 것, 책을 찾는 것 등에 해당됩니다.

선형 탐색

왼쪽부터 쭉 찾다가 원하는 값이 있다면 멈춥니다. 리스트의 처음부터 끝까지 순서대로 하나씩 탐색을 진행하는 알고리즘입니다.

아래의 코드는 선형 탐색 알고리즘의 예시 입니다.

def linear_search(element, some_list):

	for i in range(len(some_list)):
        if some_list[i] == element:
            return i
    return None
    
print(linear_search(2, [2, 3, 5, 7, 11]))
print(linear_search(0, [2, 3, 5, 7, 11]))
print(linear_search(5, [2, 3, 5, 7, 11]))

이진 탐색

중앙 값을 19이고, 29를 찾는다고 하면 19의 왼쪽에는 해당 값이 없으므로 볼 필요가 없게 됩니다. 그 후 중간 값인 37을 기준으로 왼쪽에 있으니 37 이후의 값은 볼 필요가 없습니다. 이렇게 탐색 범위를 반 씩 줄여 탐색하는 과정을 이진 탐색이라고 합니다. 이 때 정렬이 되어있다는 가정 하에 탐색이 이루어질 수 있습니다.

아래의 코드는 이진 탐색 알고리즘의 예시입니다.

def binary_search(element, some_list):

	# 시작할 때의 탐색 범위는 0부터 len(some_list) -1
	start_index = 0
    end_index = len(some_list) - 1
    
    #반복문을 돌립니다.
    while start_index <= end_index:
    	# 중간 지점
    	midpoint = (start_index + end_index) //2
        	if some_list[midpoint] == element:
           		return midpoint
           	elif some_list[midpoint] > element:
            	end_index = midpoint - 1
        	else:
            	start_index = midpoint + 1
    return None


print(binary_search(2, [2, 3, 5, 7, 11]))
print(binary_search(0, [2, 3, 5, 7, 11]))
print(binary_search(5, [2, 3, 5, 7, 11]))
print(binary_search(3, [2, 3, 5, 7, 11]))
print(binary_search(11, [2, 3, 5, 7, 11]))  

---

탐색 알고리즘 비교

선형탐색
선형탐색을 통해 값을 가장 빨리 찾는 경우는 2가 가장 왼쪽에 있으니 1번으로 가장 빨리 찾을 수 있고 54를 찾는 경우 해당 리스트에는 값이 없으니 16번이 걸린다는 것을 알 수 있습니다.

이진탐색
이진탐색을 통해 값을 가장 빨리 찾는 경우는 19로 가장 중앙 값입니다. 만약 0을 찾는다면 0은 19보다 작고, 7보다도 작고, 3보다도 작으며, 마지막 값인 2와 비교했을 때 값이 없으므로 4번이 걸림을 알 수 있습니다.

해당 차이의 결과는 아래와 같습니다.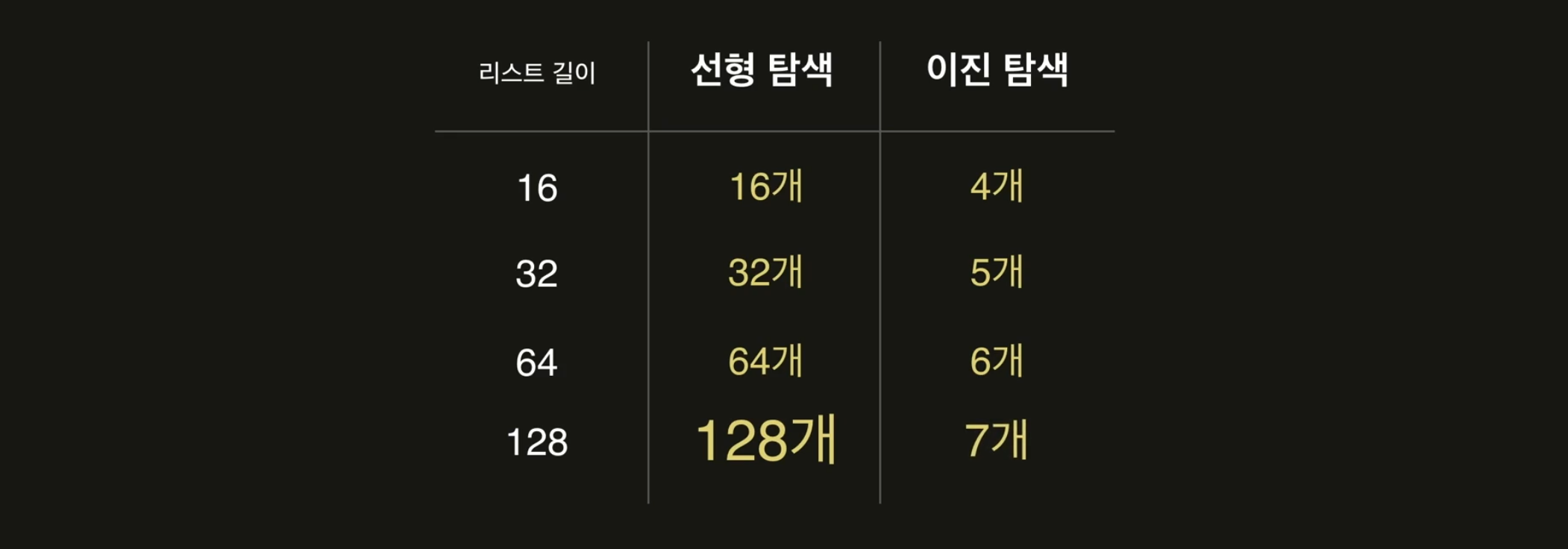

수억명, 수백만명 등 엄청난 수를 비교해야 하는 상황으로 가정할 때 선형 탐색과 이진 탐색의 비교 횟수는 엄청나게 차이남을 알 수 있습니다.

정렬 알고리즘

정렬(sorting)이란 리스트의 원소들을 특정 순서로 정리하는 것을 말합니다. 파이썬에서는 이미 sorted, sort메서드가 있는데, 왜 배워야 할까요?

정렬은 다양한 방식으로 해결할 수 있는데, 알고리즘의 기초를 다질 수 있습니다. 그리고 모든 개발자가 알아야 하는 가장 기본적인 알고리즘 입니다.

선택 정렬

선택 정렬이란 가장 먼저 생각이 날 수 있는 자연스러운 정렬 알고리즘입니다. 각 위치(인덱스)에 어떤 값이 들어갈지를 찾는데요. 가장 작은 값을 찾아 0번 인덱스에 놓고, 두번째로 작은 값을 1번 인덱스에 놓고 세번째로 작은 값을 찾아서 2번 인덱스에 놓고....이런 식으로 쭉 진행해 정렬하는 것을 말합니다.

삽입 정렬

각 값이 어떤 위치에 들어갈지를 찾는 정렬입니다.

선택 정렬과 삽입 정렬 두 가지의 정렬 알고리즘을 살펴보았는데요, 이 외에도 퀵 정렬, 힙 정렬, 거품 정렬 등 여러 정렬이 있습니다.

해당 사이트에서 상황마다의 정렬 알고리즘 퍼포먼스를 살펴볼 수 있습니다.

이미 거의 정렬된 리스트를 정렬할 때는 삽입 정렬이 가장 빠른 반면, 무작위 순서의 리스트를 정렬할 때는 힙 정렬이 가장 먼저 끝나는 것을 알 수 있습니다. 정렬된 리스트의 경우 삽입 정렬이 매우 오래 걸리고 선택 정렬과 합병 정렬은 상황에 영향을 받지 않고 일정한 시간이 걸린다는 점도 눈여겨 볼 만 합니다.

정렬의 경우 절대적인 답은 없으며, 상황에 따른 각 알고리즘의 장단점을 파악해야 올바른 알고리즘을 선택할 수 있습니다. 그렇기 때문에 알고리즘을 평가하는 능력, 알고리즘 평가법이 필요합니다.

알고리즘 평가법

평가의 두 기준

성능이나 시간이 무제한이라면 아무런 알고리즘을 사용해도 되지만 실제는 그렇지 않습니다. 그래서 시간과 공간을 신경써야 합니다.

좋은 코드의 첫 번째 기준은 얼마냐 빠르냐, 시간입니다.

두 번째는 공간, 쉽게 말해서 메모리를 적게 먹는 프로그램이 좋은 코드라고 할 수 있습니다.

시간 복잡도

사람들은 문제를 빨리 해결하는 알고리즘을 원합니다. 하지만 단순히 프로그램이 돌아가는 시간만으로 알고리즘을 평가하기는 어렵습니다. 왜냐하면 컴퓨터 사양이 낮거나, 비교적 느린 프로그래밍 언어를 사용하거나, 외부에서 무거운 프로그램을 돌릴 때마다 속도가 달라질 수 있기 때문입니다. 그래서 시간복잡도(Time Complexity)라는 개념을 사용합니다.

시간복잡도는 데이터가 많이질수록 걸리는 시간이 얼마나 급격히 증가하냐를 판단합니다.
알고리즘 B는 A에 비해 시간이 급격하게 증가합니다. 그리고 두 번째 알고리즘이 시간 복잡도가 크다고 표현합니다.

시간복잡도를 계산하기 위해서는 수학적 개념이 필요한데요, 바로 거듭제곱과 로그입니다.

점근 표기법(Big-O Notaion)

알고리즘은 인풋의 크기에 따라 달라집니다. 그래서 알고리즘을 인풋에 대한 수식으로 나타낼 수 있는데요.

리스트의 길이가 n인 알고리즘의 소요시간은 20n+40, 2n²+8n+123, 20lgn+60 등 프로그래밍 언어 등 환경에 따라 달라집니다.

그래서 다같이 약속을 한 것이 점근표기법인데요.

소요시간이 20n+40이라면 영향력있는 n에 따라 점근 표기법에서는 O(𝑛)으로 작성됩니다. 그리고 2n²+8n+123은 O(𝑛²)으로 작성됩니다. 그리고 20lg𝑛+60은 O(lg𝑛)으로 표기됩니다.

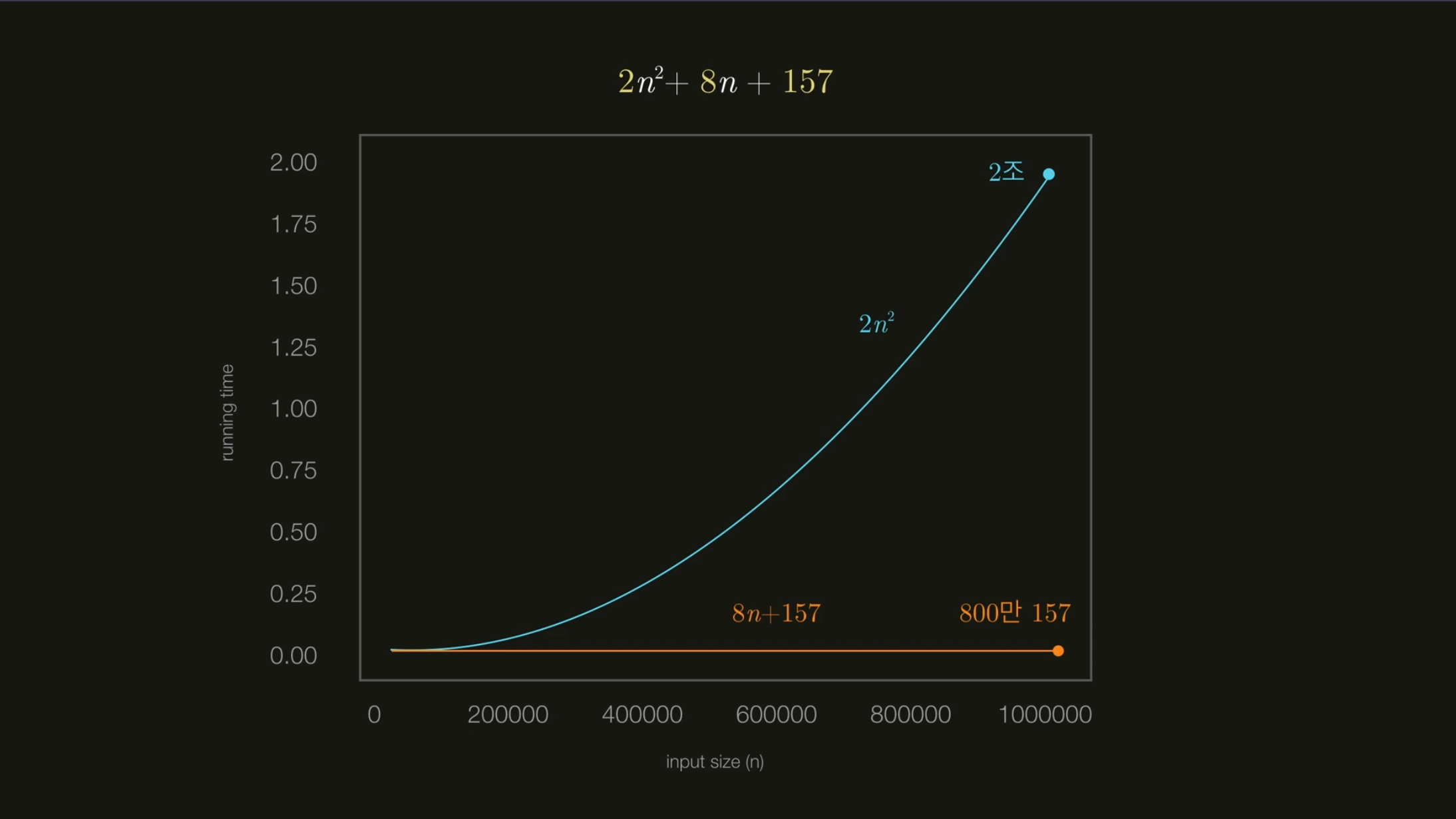𝑛이 별로 크지 않다면 안 좋은 알고리즘을 사용해도 상관없습니다. 그러나 알고리즘을 판단하기 위해서는 𝑛이 얼마냐 크냐(절대적인 시간이 아닌 성장성)를 봐야만 합니다.

점근 표기법(Big-O Notaion)의 의미

탐색 알고리즘 평가

선형탐색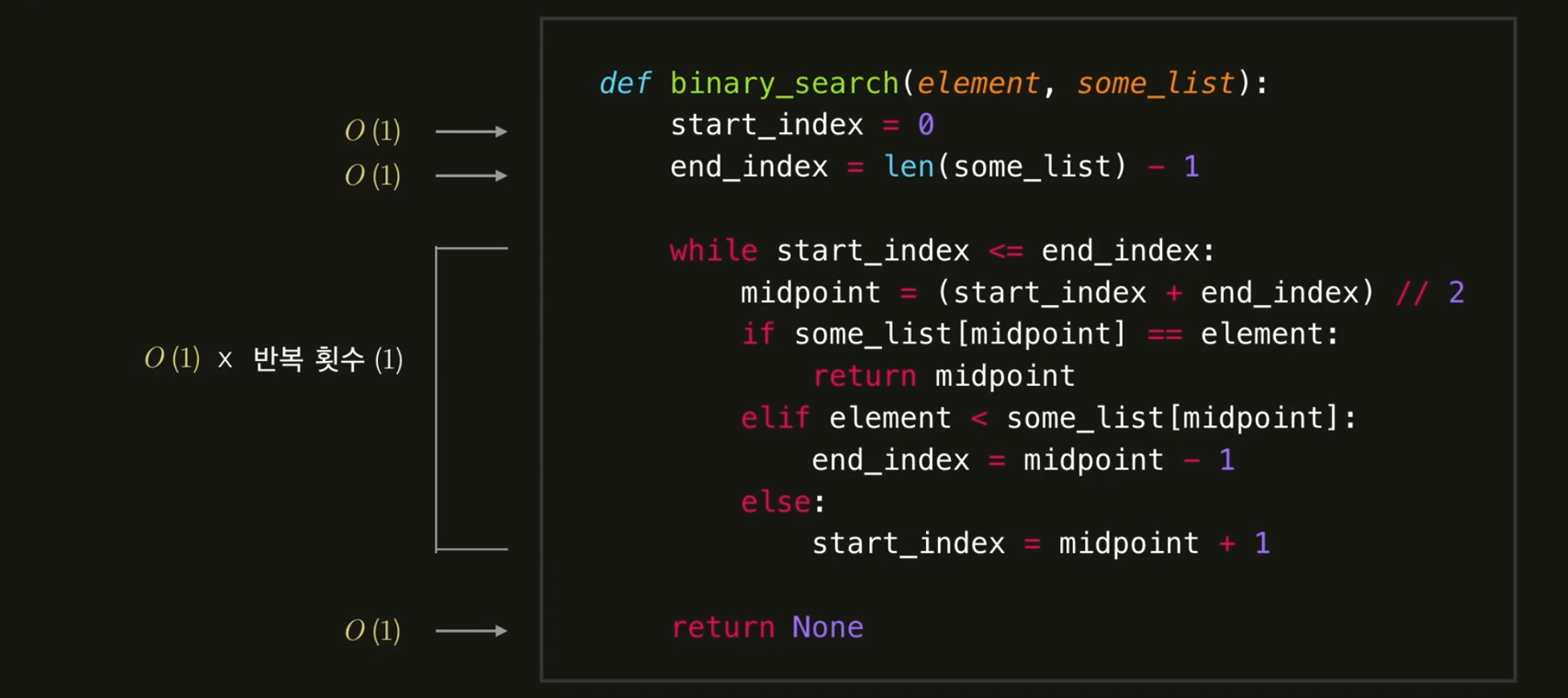최고의 경우는 O(1)+O(1)+O(1)+O(1) = O(4) = O(1)이고,
최악의 경우는 O(1)+O(1)+O(𝑛)+O(1) = O(𝑛+3) = O(𝑛)입니다.


이진 탐색

최고의 경우는 O(1)+O(1)+O(1)+O(1) = O(4) = O(1)이고,
최악의 경우는 반씩 줄어드는 탐색이니 반복문이 lg𝑛으로 O(1)+O(1)+O(lg𝑛)+O(1) = O(lg𝑛+3) = O(lg𝑛)입니다.

주요 시간 복잡도 정리

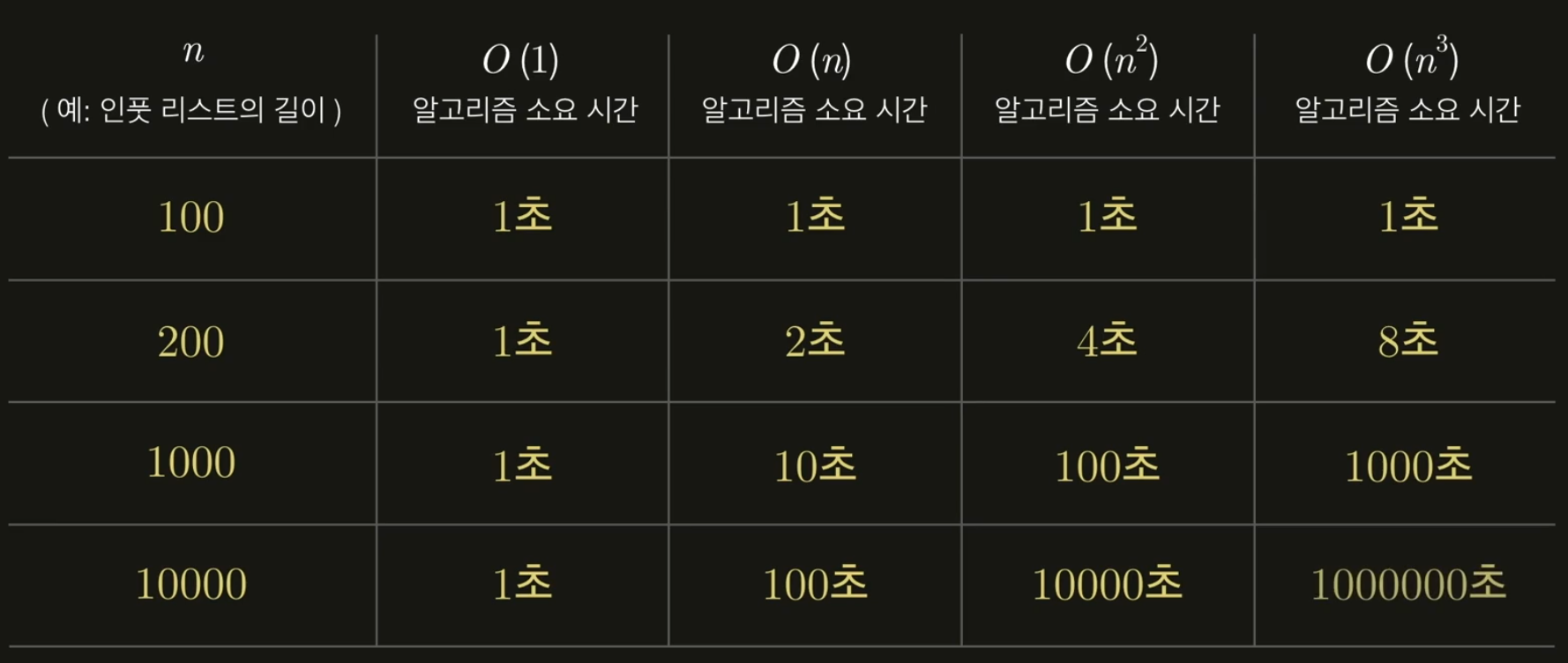
알고리즘의 시간 복잡도는 대개 이 중 하나입니다.

• O(1)
• O(𝑛)
• O(lg𝑛)
• O(𝑛lg𝑛)
• O(n!)
• O(2ⁿ)
• O(𝑛²)
• O(𝑛³)
• O(𝑛⁴)
  
  

O(1)

def print_first(my_list):
    print(my_list[0]) 

print_first([2, 3])

반복문이 없으면 대체로 O(1)입니다.

O(𝑛)

def print_each(my_list):
    for i in range(len(my_list)):
        print(my_list[i])

반복문이 있고, 반복되는 횟수가 인풋의 크기와 비례하면 일반적으로 O(n)입니다.

O(𝑛²)

def print_pairs(my_list):
    for i in range(len(my_list)):
        for j in range(len(my_list)):
            print(my_list[i], my_list[j])

반복문 안에 반복문이 있는 경우, 두 반복문 다 인풋의 크기에 비례하는 경우 O(𝑛²)입니다.

O(𝑛³)

def print_triplets(my_list):
    for i in range(len(my_list)):
        for j in range(len(my_list)):
            for k in range(len(my_list)):
                print(my_list[i], my_list[j], my_list[k])

O(𝑛²)와 동일한 원리힙니다.

O(lg𝑛)

def print_powers_of_two(n):
    i = 1
    while i < n:
        print(i)
        i = i * 2

해당 함수는 2의 거듭제곱을 출력하는 함수입니다. 만약 인풋 n이 128이다면 7번 실행되는데, lg128 = 7과 같습니다.

따라서 print_powers_of_two 함수는 O(lg𝑛)입니다.

O(𝑛lg𝑛)

O(𝑛lg𝑛)은 O(𝑛)과 O(lg𝑛)이 겹쳐진 것입니다.

def print_powers_of_two_repeatedly(n):
    for i in range(n): # 반복횟수: n에 비례
        j = 1
        while j < n: # 반복횟수: lg n에 비례
            print(i, j)
            j = j * 2

for문의 반복횟수는 𝑛²에 비례하는데, while문의 반복횟수는 lg𝑛에 비례합니다.

def print_powers_of_two_repeatedly(n):
    i = 1
    while i < n: # 반복횟수: lg n에 비례
        for j in range(n): # 반복횟수: n에 비례
            print(i, j)
        i = i * 2

다음의 경우도 마찬가지입니다.

주요 공간 복잡도 정리

O(1)

def product(a, b, c):
    result = a * b * c
    return result

파라미터 a,b,c가 차지하는 공간을 제외하면 변수 result가 공간을 차지합니다 result가 차지하는 메모리 공간은 인풋과 무관하기에 product의 공간 복잡도는 O(1)입니다.

O(𝑛)

def get_every_other(my_list):
    every_other = my_list[::2]
    return every_other

파라미터 my_list가 차지하는 공간을 제외하면 추가적으로 변수 every_other가 공간을 차지합니다.
리스트 every_other에는 my_list의 짝수 인덱스의 값들이 복사돼서 들어갑니다. 약 𝑛/2 개의 값이 들어가기에 공간 복잡도는 O(𝑛)입니다.

O(𝑛²)

def largest_product(my_list):
    products = []
    for a in my_list:
        for b in my_list:
            products.append(a * b)
    
    return max(products)

파라미터 my_list가 차지하는 공간을 제외하면 추가적으로 변수 products, a, b가 공간을 차지합니다.

우선 a와 b는 그냥 정수 값을 담기 때문에 O(1)입니다. 리스트 products에는 my_list에서 가능한 모든 조합의 곱이 들어갑니다. 그래서 총 𝑛²개의 값이 들어가며 공간 복잡도는 O(𝑛²)입니다.