Likelihood(가능도)

Likelihood(가능도)

데이터가 특정 분포로부터 만들어졌을(generate) 확률을 말합니다.
다시 말해서 어떤 값이 관측되었을 때, 해당 관측값이 어떤 확률분포로부터 나왔는지에 대한 확률이다.
ex) X = [1, 1, 1, 1, 1] 일때 그림과 같은 두 분포가 있다면

X데이터는 왼쪽 분포를 따를 가능성이 높을 것입니다.
이런 상황을 왼쪽 분포의 데이터 X에 대한 likeihood가 높다고 표현 할 수 있습니다.
likelihood 식은 다음과 같습니다.

$L(\Theta) = p(X|\theta)$ -> likeihood 표현식, $\Theta$의 parameter를 가지고 있는 정규분포

Maximum Likelihood Estimation(최대 가능도 추정)

"최대 가능도 추정"이란 것은 각 관측값 X에 대한 총 가능도(즉, 모든 가능도의 곱)가 최대가 되게 하는 확률분포를 찾는 것이라고 할 수 있습니다. 여기 가능도를 최대가 하는 값은 밑에 그림과 같습니다.

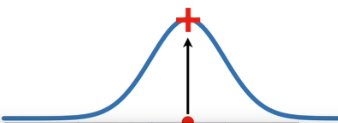
여기서 중요한점은 최대 가능도 추정(Maximum Likelihood Estimation)시, 먼저 임의의 확률분포를 가정해야 합니다.
이해를 돕기 위한 예시로 정규문포를 가정하고 최대 가능도 추정에 대해서 설명하겠습니다.

위와 같은 여러개의 관측값들이 존재항 경우, 이렇개 관측할 가능성이 가장 높은 확률 분포를 찾는다고 가정하겠습니다.
찾고자 하는 확률분포가 정확히 뭔지는 모르지만, "정규분포"라고 가정했다. 그러므로 정규분포의 평균을 조금씩 증가 시킬때 마다 가능도가 어떻게 변하는지 확인해보면 다음과 같습니다.

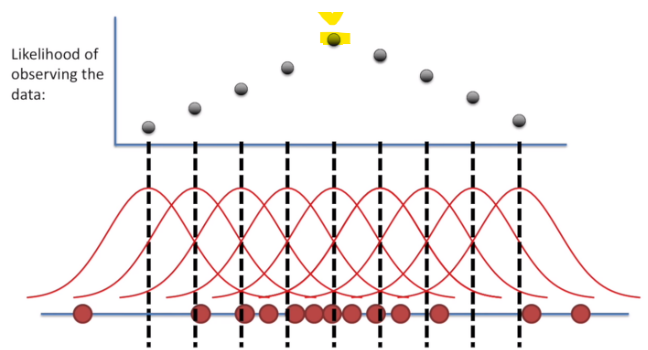
위 그림을 통해, 우리가 수집한 관측값들이 나올 수 있는 가장 가능성 높은(즉, 가장 가능도가 큰) 확률분포는 검은 제일 높이 위치한(그림에서 노란색으로 표시된 부분) 정규분포로부터 온 것이라고 추정할 수 있다. 이러한 방식을 "최대 가능도 추정"이라고 합니다.

Referece
https://data-scientist-brian-kim.tistory.com/91
https://process-mining.tistory.com/93