1. 문제로 알아보기
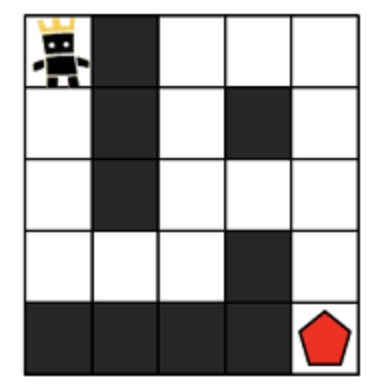
<출처 : https://programmers.co.kr/learn/courses/30/lessons/1844#qna >
간단한 문제이다. (1,1)에서 시작하여 대각선 끝인 (n,m)에 도착하는 최단 경로를 구하는 문제이다. 코딩테스트 공부를 해본 사람이라면 누구든지 dfs,bfs를 떠올 릴 수 있을 그런 흔한 문제이다. 그런데 여기서 dfs와 bfs를 고민한다면 이는 공부를 조금 소홀히 한 사람이라고 할 수 있다.
그렇다,, 그게 바로 나다...
자 다시는 이러한 문제로 혼동하지 않기 위해서 이렇게 기록을 남긴다.
2. 첫 시도,, DFS
import copy
import sys
def dfs(maps,cur,pre_visited,depth) :
global dist, row, col
x,y = cur
visited = copy.deepcopy(pre_visited)
visited[x][y] = 1
if cur == (row-1,col-1) :
dist = min(dist,depth)
return
for dx,dy in (-1,0) , (0,1) , (1,0) , (0,-1) : #위 , 오, 아 ,왼
nx,ny = x+dx,y+dy
if (0 <= nx < row) and (0 <= ny < col) and maps[nx][ny] != 0 and visited[nx][ny] != 1 and depth+1 < dist :
dfs(maps,(nx,ny),visited,depth+1)
def solution(maps):
sys.setrecursionlimit(10**7)
global dist, row, col
dist = 10**8
row = len(maps)
col = len(maps[0])
visited = [[0]*col for _ in range(row)]
dfs(maps,(0,0),visited,1)
return -1 if dist == 10**8 else dist첫 시도는 dfs 였다.
내 생각은 dfs로 모든 경로를 탐색하여 경로마다 길이가 나오면 이것이 최소의 경로인지를 확인 해 주는 것이다 ㅎ
지금 적으면서 생각 해보면 얼마나 짧은 생각 일까..
그렇다 dfs로 푼다면 정답은 나온다! 다만 효율성 테스트가 있는 문제라면 이 접근 방식은 10000% 실패이다..
3. 그렇다면? BFS는
사실 최단 경로 문제의 정석은 bfs이다. 왜냐하면 일단 방문 했던 노드를 재 방문 할 필요가 없다. 그리고 도착지에 도달하는 순간 다른 경로는 고민할 필요가 없다. 그 경로가 바로 최단 경로 이기 때문이다.
아래 그림을 보면 DFS와 BFS 방법으로 최단경로를 풀시 효율성에 대해 고민 해 볼 수 있게 된다.
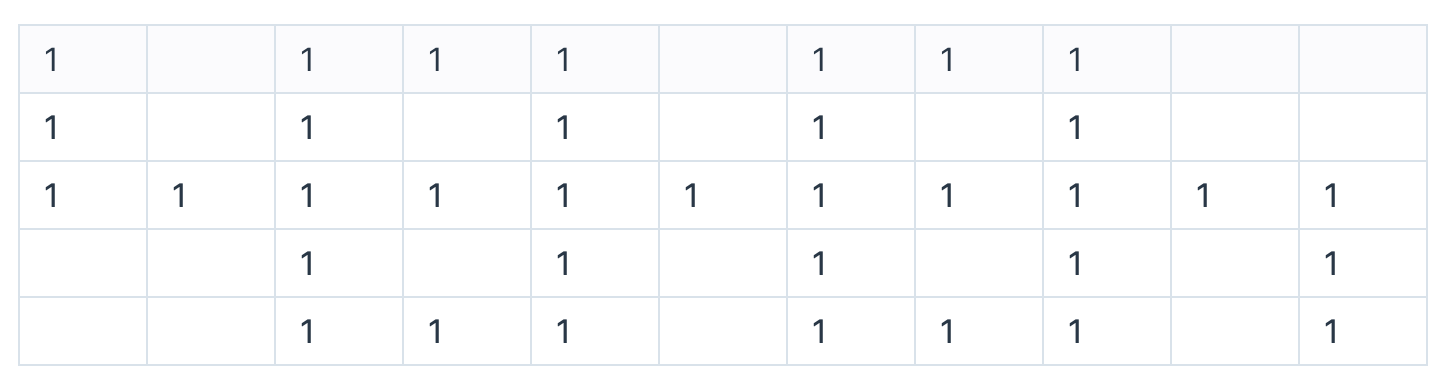
1로 체크된 곳이 길이며, 없는 곳은 벽이다.
자 dfs 로 탐색하게 되다면 얼만 큼의 노드를 방문해야 하는가?
dfs : 4 + 13 * 3 **2 + 1 + 4 이다.
여기서 dfs의 문제를 알 수 있다. 분기점이 생길때마다 끝까지 갔다가 다시 그 분기점으로 돌아와야 한다...
그렇다면 지금 처럼 삼거리가 2개가 아니라 1000개라면??
dfs : 4 + 13 * 3 **1000 + 1000 + 4
13 * 3의 1000 승 ㅋㅋㅋ... 시간 복잡도면에서 효율적이지 않다고 말할 수 있다.
반대로 bfs는 ?? 간단하다 모든 노드의 수만큼만 방문하면 된다.
bfs : 4 + 13*2 + 1 + 4 이다.
이 역시, 위 그림에서 bfs로 삼거리가 1000개인 미로를 탐색한다면
bfs : 4 + 13*1000 + 1000 + 4 이다.
역시! 숫자로 체감한는게 가장 빠른 듯하다.. ㅎ
이처럼 최단 경로 문제에서는 bfs가 dfs 보다 더 효율적이게 답을 구할 수 있는 듯 하다.
답을 구하는지 못하는게 아니다. 효율적이게 구하지 못할 뿐!
4. BFS 탐색 시 주의사항!
(1)
while queue :
x,y,depth = queue.popleft()
visited[x][y] = 1
if (x,y) == (row-1,col-1) :
return depth
for dx,dy in (1,0),(0,1),(0,-1),(-1,0) :
nx,ny = x+dx,y+dy
if 0<=nx<row and 0<=ny<col and /
maps[nx][ny] != 0 and visited[nx][ny] ==0 :
queue.append((nx,ny,depth+1))(2)
visited[0][0] = 1
while queue :
x,y,depth = queue.popleft()
if (x,y) == (row-1,col-1) :
return depth
for dx,dy in (1,0),(0,1),(0,-1),(-1,0) :
nx,ny = x+dx,y+dy
if 0<=nx<row and 0<=ny<col and /
maps[nx][ny] != 0 and visited[nx][ny] ==0 :
visited[nx][ny] = 1
queue.append((nx,ny,depth+1))(1)번과 (2)번 코드의 차이점이 무엇인지 보이는가?
방문체크를 어디서 하느냐의 차이가 보일 것이다!
그렇다면 무엇이 더 효율적인 코드일까 한번 잠시 생각 해 보길 바란다!
이 역시 마찬가지로 둘다 정답은 나올 수 있는 코드이다. 하지만 (1)번의 경우 bfs의 특성을 잘 살리지 못한 코드라 할 수 있다.
큐에서 pop을 진행하고 나서 해당 영역을 방문 체크 한다면, 무엇이 문제인가?
예시를 들겠다.
A와B가 같은 너비에 현재 큐에 들어 있는 노드라고 했을 시, A를 먼저 pop하고 방문했다고 하자. A로 부터 연결되는 노드에 B가 있다면 B는 큐에는 있지만, 방문하지 않은 노드이기에 중복적으로 큐에 넣을 것이다. 그렇다면 bfs는 노드 수만큼 반복 하는 것이 특징인데, 중복되는 노드를 방문하는 경우가 생기게 되는 것이다.
이처럼 같은 정답을 내는 코드라도 조금 더 효율적이게 생각하면서 개념을 이해할 필요가 있다고 생각한다...
5. DFS,BFS 응용/활용 문제 정리 :
DFS, BFS은 특징에 따라 사용에 더 적합한 문제 유형들이 있다.
그래프의 모든 정점을 방문하는 것이 주요한 문제
단순히 모든 정점을 방문하는 것이 중요한 문제의 경우 DFS, BFS 두 가지 방법 중 어느 것을 사용하셔도 상관없다.
- 경로의 특징을 저장해둬야 하는 문제 예를 들면 각 정점에 숫자가 적혀있고 a부터 b까지 가는 경로를 구하는데 경로에 같은 숫자가 있으면 안 된다는 문제 등, 각각의 경로마다 특징을 저장해둬야 할 때는 DFS를 사용한다. (BFS는 경로의 특징을 가지지 못함)
- 최단거리 구해야 하는 문제
미로 찾기 등 최단거리를 구해야 할 경우, BFS가 유리하다.
왜냐하면 깊이 우선 탐색으로 경로를 검색할 경우 처음으로 발견되는 해답이 최단거리가 아닐 수 있지만,너비 우선 탐색으로 현재 노드에서 가까운 곳부터 찾기 때문에경로를 탐색 시 먼저 찾아지는 해답이 곧 최단거리기 때문.
이밖에도
- 검색 대상 그래프가 정말 크다면 DFS를 고려
- 검색대상의 규모가 크지 않고, 검색 시작 지점으로부터 원하는 대상이 별로 멀지 않다면 BFS를 고려하는 것이 좋다.