본 글의 내용은 Operating Systems: Three Easy Pieces의 Free Space Management 챕터를 정리한 것입니다.

☑️ 개요

• 메모리 여유 공간(free space)을 관리하는 것은 사실 쉬울 수도 있다. 관리 대상 공간이 고정된 크기로 나뉘어져 있다면, 고정 크기 단위의 목록을 보관하면 된다.

• 더 어려워지는 경우는 여유 공간이 가변 크기 단위로 구성될 때이다. 메모리 할당 라이브러리(malloc 등)나 세그멘테이션을 사용하는 OS가 그 경우인데, 여유 공간의 크기가 작은 조각으로 쪼개져 연속된 여유 공간이 없어지는 외부 단편화가 발생한다.

• 이런 경우 여유 공간은 어떻게 관리해야 하는가? 단편화를 최소화하기 위해 어떤 전략을 사용하는가? 각 접근 방식의 소요 시간과 공간 오버헤드는 얼마나 되는가?

☑️ 가정

• 라이브러리가 관리하는 공간을 힙이라고 하며, 힙을 관리하는 데 사용하는 데이터 구조는 일종의 여유 목록(free list)이다. 이것은 메모리 공간에 존재하는 모든 여유 공간을 참조한다.

• 물론 여유 목록은 List 형태일 필요는 없으며, 데이터 구조일 뿐이다.

• 여기서 메모리가 클라이언트에 전달된 후, 다른 위치로 재배치 할 수 없다고 가정해보자. (free 를 호출하기 전까지는)

• 재배치가 불가한 상황에서 세그멘테이션을 활용했다면 compaction을 통해 외부 단편화를 줄일 수 없게 되는 것이다.

• 한 가지 가정을 더해보자. 메모리 할당자가 관리하는 공간이 연속적이면서 고정된 크기의 단위로 나뉘어져 있다면 어떨까?

☑️ Low level mechanism

• 대부분의 메모리 할당자에서 쓰이는 공통적인 메커니즘이 존재한다.

• 첫째로 분할 및 병합(splitting & coalescing) , 둘째로 빠르고 쉽게 여유 공간 찾기, 셋째로 간단한 목록으로 여유 공간 구분하기 이다.

▶️ 분할 및 병합

• 단편화가 존재하는 상황을 배제하고, 확보 가능한 여유 공간보다 작은 공간이 요청되면, 존재하는 여유 공간을 쪼개서(분할) 반환하고, 남은 여유 공간은 여유 목록에 남긴다.

• 추후 사용 공간을 해제하면 해당 공간의 주변에 여유 공간이 있는지 확인하고, 그것들을 합친다. (병합)

▶️ 할당된 영역 크기 추적

• 메모리를 해제하는 free(void *ptr) 함수는 해제할 크기를 전달 받지 않고, 오직 포인터만으로 해제할 메모리를 결정할 수 있다.

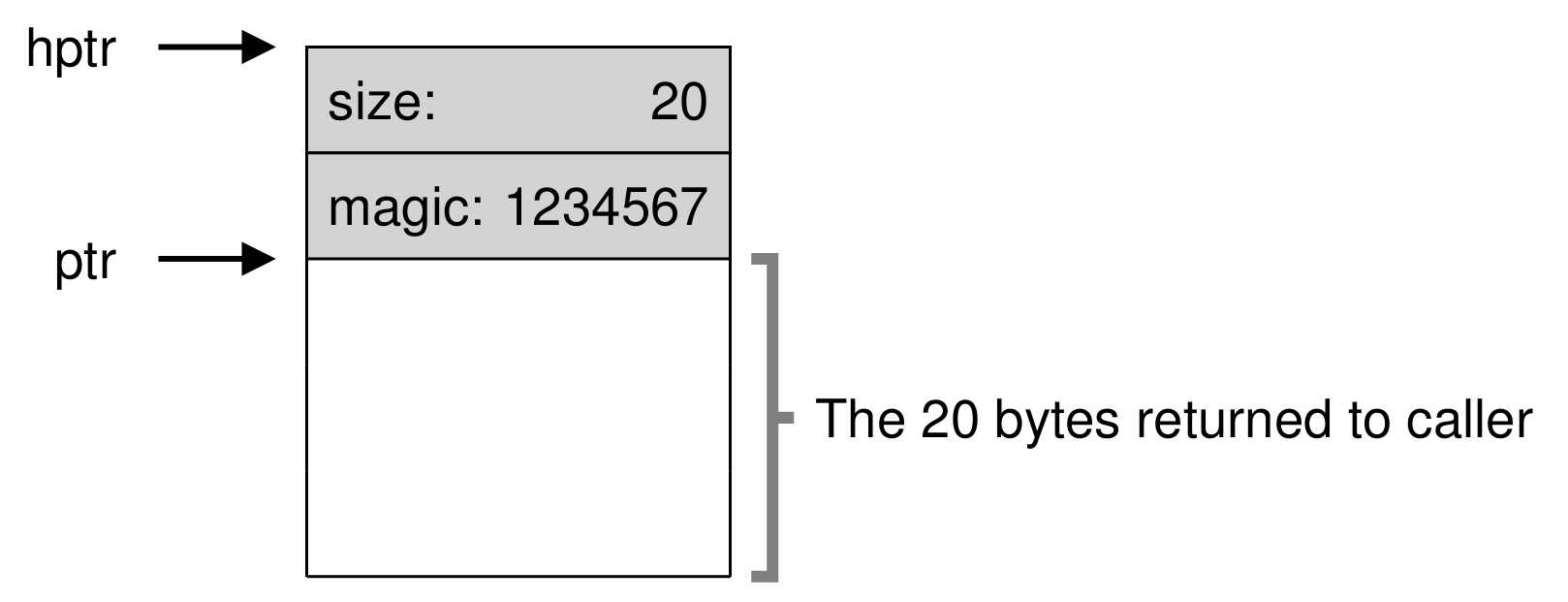
• 이것을 위해 대부분의 메모리 할당자는 추가 정보를 블록의 헤더에 저장한다.

• 헤더에는 최소한 할당 영역의 크기만큼은 기록되며, 해제 속도를 높이기 위해 추가적인 포인터 정보, 무결성 검사를 위한 매직 넘버 등이 기록된다.

• ptr 에 수를 차감하는 연산을 하면 헤더의 시작 위치를 얻을 수 있는데, 이것으로 헤더의 정보를 추출할 수 있다.

• 이렇게 메모리 영역의 정보를 위해 헤더가 함께 공간을 차지하며, N 크기의 여유 공간이 요청되면 (N + 헤더의 크기)의 여유 공간이 존재하는지 검색한다.

▶️ 여유 목록 끼워넣기

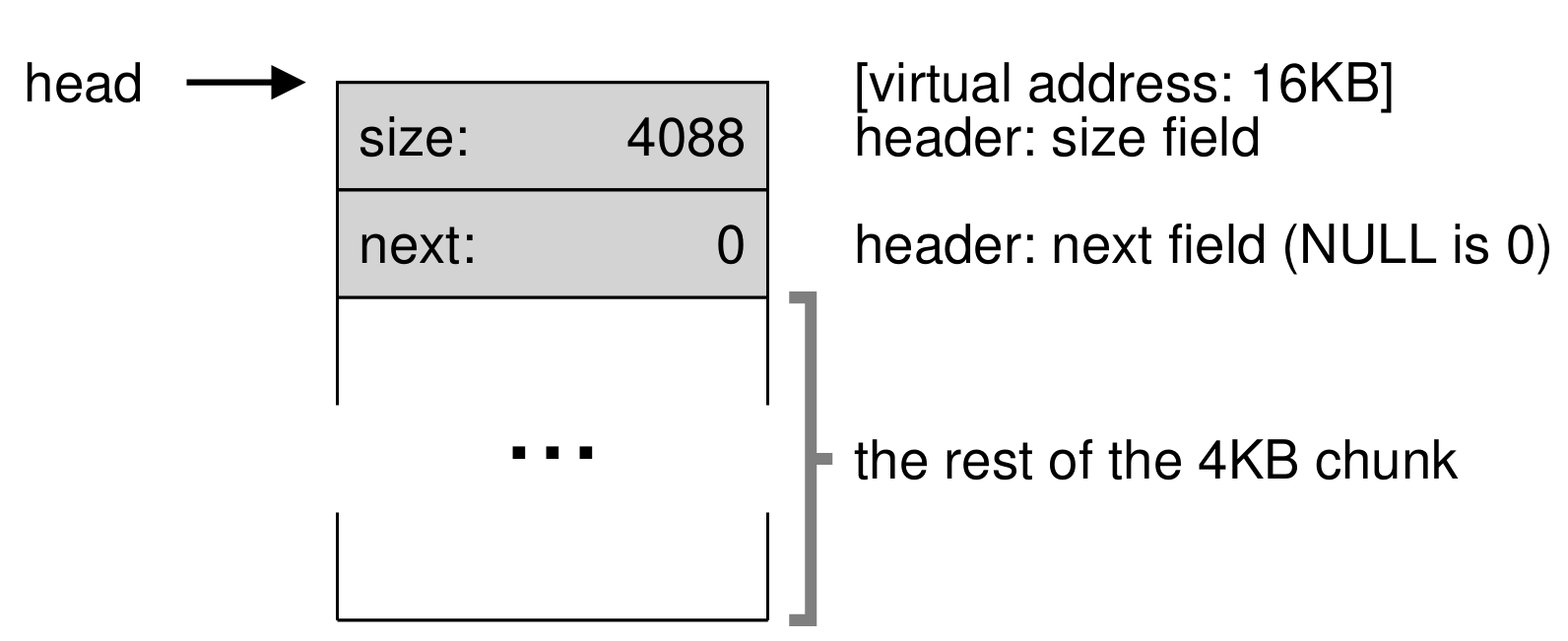
• 4KB의 힙 공간을 초기화했을 때, 위와 같은 형태를 띄게 된다.

• 위 상태에서 100바이트의 메모리 공간이 요청되면, 100바이트를 수용할 수 있는 큰 덩어리를 찾을 것이다. 여기서는 크기 4088의 덩어리가 선택된다.
  

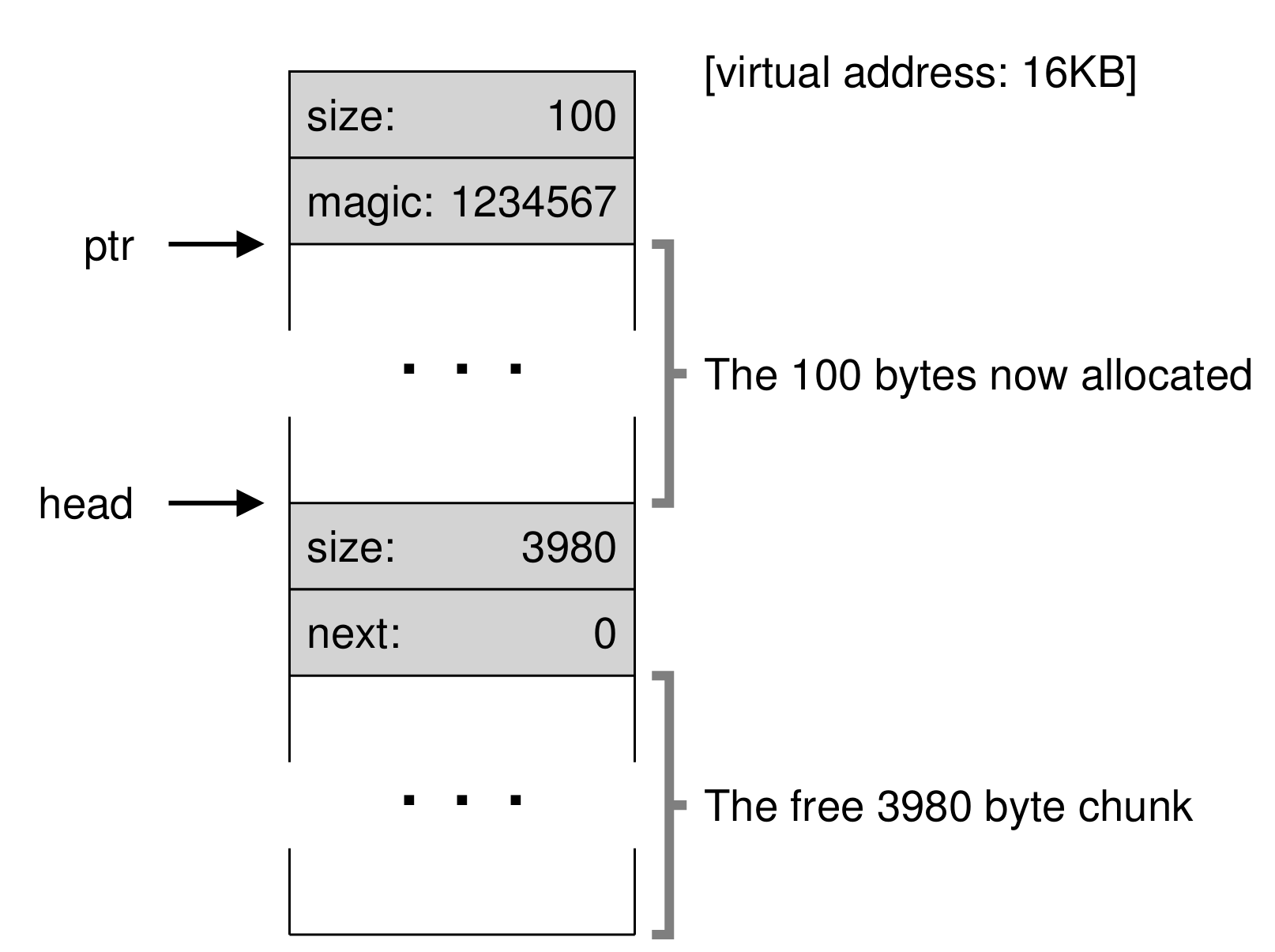
• 그러면 요청을 처리할 수 있을 만큼의 크기와 나머지 크기로 쪼개지면서 위와 같은 형태가 된다.

• 여기에는 8바이트의 헤더가 사용되기 때문에, 결과적으로 100바이트 요청에 실제로 108바이트를 사용했다.

• 나머지 크기는 (4088-108)로, 3980 바이트 만큼의 여유 공간으로 남게 된다.
  

• 위처럼 여러 공간이 할당된 상태에서, 중간의 100바이트가 해제된다면 어떨까?

• 그럼 할당공간-여유공간-할당공간-여유공간의 형태로, 공간이 파편화된다. 이것은 흔히 발생하는 현상이기도 하다.

• 만약 세 개의 100바이트 중 연속된 두개가 해제되었다면, 인접한 공간이므로 병합(merge)할 수 있다.

▶️ 힙 늘리기

• 힙의 공간이 부족하면 어떻게 해야할까?

• 가장 간단한 방법은 NULL을 반환하고 실패하는 것이다.

• 대부분의 메모리 할당자는 OS에게 메모리를 요청한다. 이것은 일종의 시스템 호출(예로 UNIX의 sbrk 가 있다)을 통한 힙 확장이며, 확장된 공간에서 여유 공간을 반환한다.

• OS가 사용 가능한 물리 페이지를 찾아 프로세스의 주소 공간에 맵핑하고, 새 힙의 끝 값을 반환한다.

☑️ 기본적인 전략

• 이상적인 메모리 할당자는 빠르면서, 단편화를 최소화할 것이다.

• 하지만 메모리 할당과 해제 요청은 일정하지 않기 때문에, 잘못된 입력이 들어오면 어떤 전략을 써도 나쁜 결과를 낼 수도 있다.

• 그러므로 최적의 전략을 찾기보다는, 기본적인 전략의 장단점에 대해 알아보도록 한다.

▶️ Best-Fit

• 여유 공간에서 요청 크기 이상의 덩어리들을 찾고, 그 중 가장 작은 값을 선택하는 전략이다. 고로 공간 효율적이다.

• 여유 목록을 한 번 전체 탐색하는 것으로 찾아낼 수 있다.

• 단순하게 구현한다면, 전체 탐색이라는 조건이 큰 성능 저하를 야기한다.

▶️ Worst-Fit

• Best-Fit과 정반대의 접근으로, 가능한 큰 공간을 사용한다.

• 그래서 작은 조각이 생기는 것을 방지하고, 선택한 공간 이외의 큰 공간들을 남길 수 있게 된다.

• Best-Fit과 동일하게 전체 검색은 성능 하락을 야기하기 때문에, 성능이 좋지 않다.

• 또한 대부분의 연구결과에서 단편화를 많이 일으키는 것으로 밝혀졌다.

▶️ First-Fit

• 사용 가능한 첫번째 공간을 바로 사용하는 것으로, 완전 탐색보다 나은 성능을 보인다.

• 그러나 작은 여유 공간이 여유 목록의 앞에 포진하면 문제가 되고, 관리 방식이 중요해진다.

• 그래서 여유 공간을 주소 값을 기준으로 정렬하여 관리하기도 한다. (병합이 가능한 시점에 유리하므로)

▶️ Next Fit

• First-Fit과 유사하나, 마지막에 선택한 위치를 기록해두고, 탐색이 재개될 때 해당 위치에서 시작한다.

• 이 접근 방식으로 목록의 앞 부분에 단편화가 일어나는 것을 방지한다.

☑️ 기타 접근 방식

▶️ 분리된 목록 (Segregated lists)

• 만약 특정 앱이 자주 사용하는 크기의 요청이 몇몇 개 있다면, 해당 크기의 객체를 관리하기 위한 별도의 목록을 유지할 수 있다.

• 이런 접근 방법은 단편화에 대한 우려를 줄일 수 있고, 메모리 할당 요청을 빠르게 처리할 수 있어 진다.

• 당연하게도 기존 방식보다는 복잡할 수 밖에 없는데, 분리된 목록에 얼마 만큼의 메모리를 할당할 것인지도 문제가 된다.

• 이러한 문제를 Jeff Bonwick의 Slab 할당자가 상당히 좋은 방식으로 처리하는데, 이 할당자는 자주 요청될 가능성이 있는 커널 객체를 준비하는 객체 캐시를 사용한다.

• 이 캐시에 여유 공간이 부족해지면 일반 메모리 할당자에게 메모리를 요청하고, 캐시 내의 객체에 참조 수가 0에 가까우면 메모리를 회수시킬 수도 있다.

• 또한, 이 캐시에는 여분의 객체들을 미리 초기화된 상태로 유지하는 것으로, 객체의 초기화 및 소멸 비용을 줄인다.

▶️ 버디 알고리즘

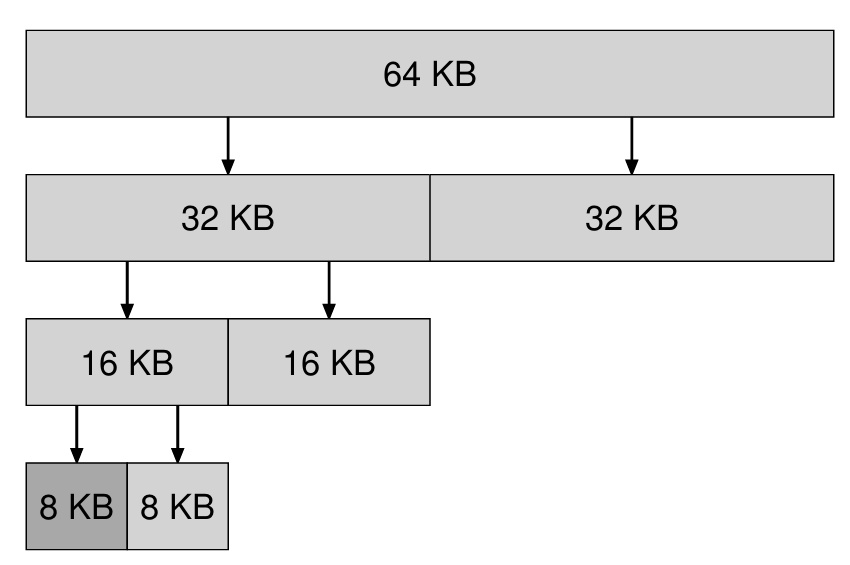
• 메모리 할당 과정에는 병합도 중요하기 때문에, 병합 과정을 단순화 하기 위해 이분 버디 할당자를 활용할 수 있다.

• 메모리는 2^N 크기의 큰 공간이라고 할 수 있는데, 메모리 할당 요청이 올 때마다 적절한 크기가 될 때까지 반으로 쪼개는 것이 이것의 접근 방식이다. (쪼개진 공간도 2^N 크기이므로, 내부 단편화 문제가 발생할 수 있다)

• 이 접근 방식의 장점은, 메모리가 해제됐을 때 병합이 쉽다는 것이다. 해제된 공간이 자신과 동일한 크기(버디)의 덩어리가 있는지 확인하고, 있으면 병합된다. 병합이 멈출 때까지 재귀적으로 진행한다.

• 또한 버디를 찾는 것은 쉬울 수 밖에 없는데, 공간이 계속해서 2로 나뉘어졌으므로 버디의 주소도 한 비트(2로 나누기 = 한번 시프트)밖에 차이가 안 난다.

▶️ 기타 아이디어

• 지금까지 설명한 많은 접근 방식들은 확장성이 부족하고, 특히 검색 속도가 느릴 수도 있다는 문제가 있다.

• 그래서 더 복잡한 자료 구조를 사용해서 성능을 높이고, 복잡성이 증가한다.

✅ 요약

• 메모리 할당에는 다양한 방식이 있고, 각자 장단점이 있다.

• 근본적으로 공간을 나누고, 다시 합치는 접근 방식이 활용된다.

• 할당된 메모리 공간의 헤더에 메타데이터를 저장하는 것으로, 공간을 얼마나 사용하는지 인지하고, 메모리를 빠르게 해제할 수 있다.

• 메모리 할당에는 Best-Fit, First-Fit 등 다양한 방식이 있으며, 단순한 방식은 성능 저하를 야기하고, 성능을 높이면 복잡성이 증가한다.

• 메모리 할당을 위해 여유 목록과 별개로 관리되는 목록을 더 활용할 수 있다.

• 결과적으로 주로 처리하는 작업이 어떤 유형인지 잘 이해할 수록 적합한 방식을 사용할 수 있게 된다.