
🧭 문제 분석
1이상 50이하의 N과,
루트 노드와 i만큼의 거리를 이루는 노드들의 개수를 담은 배열 cnt가 주어진다.
cnt 배열에 적합한 트리 중에서, 최대 트리 지름을 구해야 된다.
✅ 문제 풀이
문제 초반에는 고민이 많았는데, 사실 트리 지름을 최대한 늘리는 방법은 하나다.
분기할 때 최대한 많은 노드에 분산해서 늘리는 것이다.
예시로 2 2와 같은 입력이 주어진다면,
문제에 설명돼있는 것처럼 왼쪽이 아니라 오른쪽처럼 분기시켜야 한다.
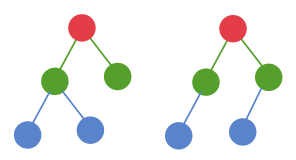
그런데 저렇게 분기시킬 수 없는 경우가 딱 한가지 존재한다.
간선을 하나만 연장해야 되는 경우이다. (cnt[i] == 1)
그래서 문제 예시에도 그런 경우가 주어지고 있다.
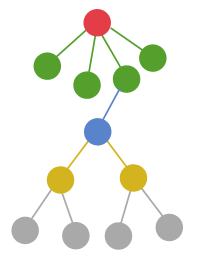
이 경우만 잘 고려해서 코드를 작성하면 될 것 같다.
우선 저 시점이 오기 전까지는 계속 분기를 하면 된다.
저 시점이 왔을 때 문제가 생길 수 있는 예시는 다음과 같다.
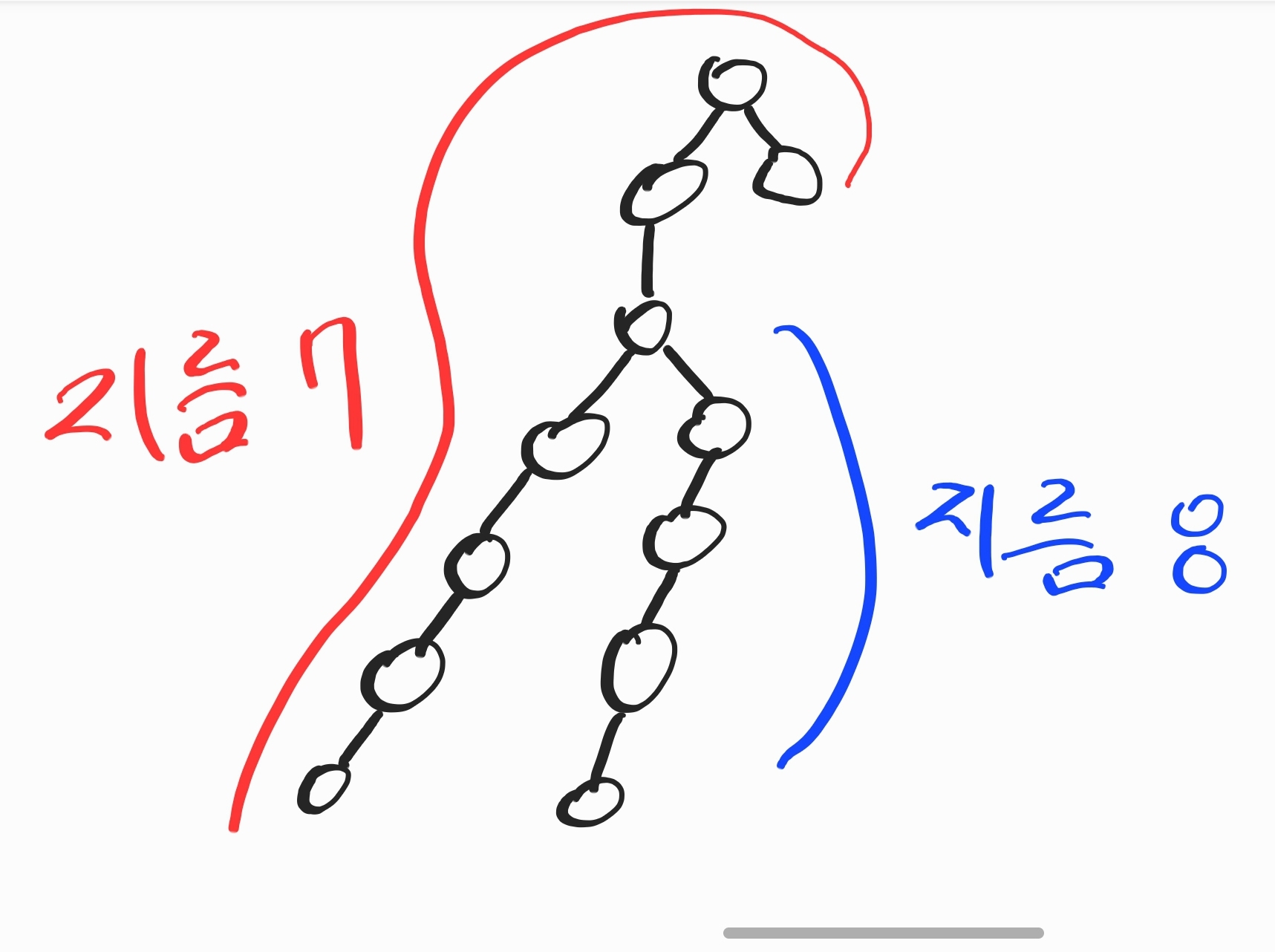
위 그림은 2 1 2 2 2 2 의 예시라고 할 수 있다.
계속 두 갈래로 분기하다보면, (가장 깊은 곳의 노드~상위에 존재하는 어느 노드) 까지의 길이보다
새롭게 계속 분기되던 두 노드의 지름이 더 길어지게 된다.
그래서 cnt[i] == 1을 만나기 전까지 계속 분기되는 지름의 길이를 기록하다가,
그 순간에 지금까지 가장 길었던 지름의 길이와 비교해서 새롭게 갱신해주어야 한다.
위 논리로 코드를 작성한다면 문제는 끝났다
우선 입력을 받는다.
val N = readLine().toInt()
val cnt = readLine().split(" ").map(String::toInt)
...이제 최대 지름 길이를 기록할 변수와
분기되면서 점점 늘어나는 지름의 길이를 기록할 변수를 선언한다.
...
var prevMax = 0
var seperated = 0
...cnt를 순차탐색해나가면서 앞서 말한 논리를 적용하자.
...
for (i in cnt.indices) {
prevMax++ // 가장 긴 지름에 하나 더 붙이기
if (cnt[i] == 1) { // 더 연장할 수 있는 게 한 곳 뿐임
// 계속 분기하던 구간과 지금까지 가장 길었던 구간을 비교
prevMax = maxOf(prevMax, seperated + 1)
seperated = 0 // 초기화
} else {
// 차기 지름 후보값에는 계속해서 더해준다 (노드가 2개 이상 연장되므로 지름은 2 증가한다)
seperated += 2
}
}
...마지막에 seperated와 prevMax 값을 비교해서 출력하면 정답
...
print(maxOf(prevMax, seperated))