
🥸 문제 분석
DP 단골 손님으로 알려진 타일링 문제이다.
조금 다른 점은 대칭으로 구성되는 타일은 제외해야 된다.
타일의 구성을 문자열과 같은 형태로 모두 기록하는 방법을 떠올려보자.
그것을 전부 기록하는 것은 메모리 제한에도 어긋날 확률이 높고 DP의 취지와는 거리가 있다.
어떻게 해야 대칭 타일만 제외하고 경우의 수를 셀 수 있을까?
✏️ 문제 풀이
우선 대칭만 제외하기 전에 그냥 모든 타일 구성의 경우의 수를 구해보자.
타일링 문제를 이미 풀어보았다면 점화식을 떠올리는 것은 어렵지 않다.
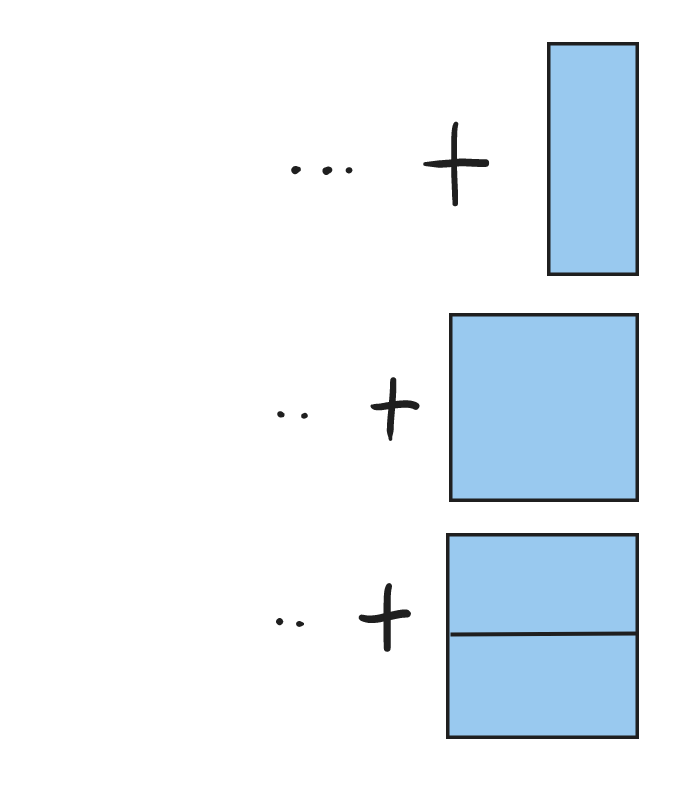
가로 N 길이의 타일 구성을 만들 것이라면,
N-1 길이의 타일 구성에 2x1 타일을 덧붙이는 경우와
N-2 길이의 타일 구성에 2x2, 1x2(2개) 타일을 덧붙이는 경우가 존재한다.
그래서 점화식은 아래와 같이 얻을 수 있다.
dp[N] = dp[N-1] + dp[N-2] * 2그럼 여기서 대칭 타일 구성은 어떻게 제외해야 될까?
우선은 N=4 정도까지의 타일 구성을 직접 그려보자.

N=3부터 대칭을 이룰 수 있는 타일이 등장하고 있다.
그러나 중앙 타일을 기준으로 완전히 대칭을 이루는 타일 구성은 중복되지 않고, 하나만 존재한다.
즉, 전체 타일 구성에서 중앙을 기준으로 완전히 대칭을 이루는 타일은 제외하고 대칭을 이룰 수 있는 타일을 제거해야 되는 것이다.
위 사진에서 형광펜으로 표시된 타일 구성이 대칭을 이룰 수 있는 유일하지 않은 타일 구성들이다.
그럼 중앙을 기준으로 완전히 대칭을 이루는 타일을 구한다는 가정하에, 어떤 계산을 해야 답을 구할 수 있을까?
동그라미 표시한 타일 구성의 개수를 보면 답이 나온다.
완전히 대칭을 이루는 타일 구성을 제외하고 나머지 중복 타일 구성의 절반이 사라져야 한다.
즉, 우리가 구해야 하는 답은
(전체 타일 구성 개수) - (전체 타일 구성 개수 - 유일한 대칭 타일) / 2이다.
위 내용이 이해가 됐다면 이제 유일한 대칭 타일 개수를 구하자.
이것도 그림을 그리면 이해가 더 쉽다.
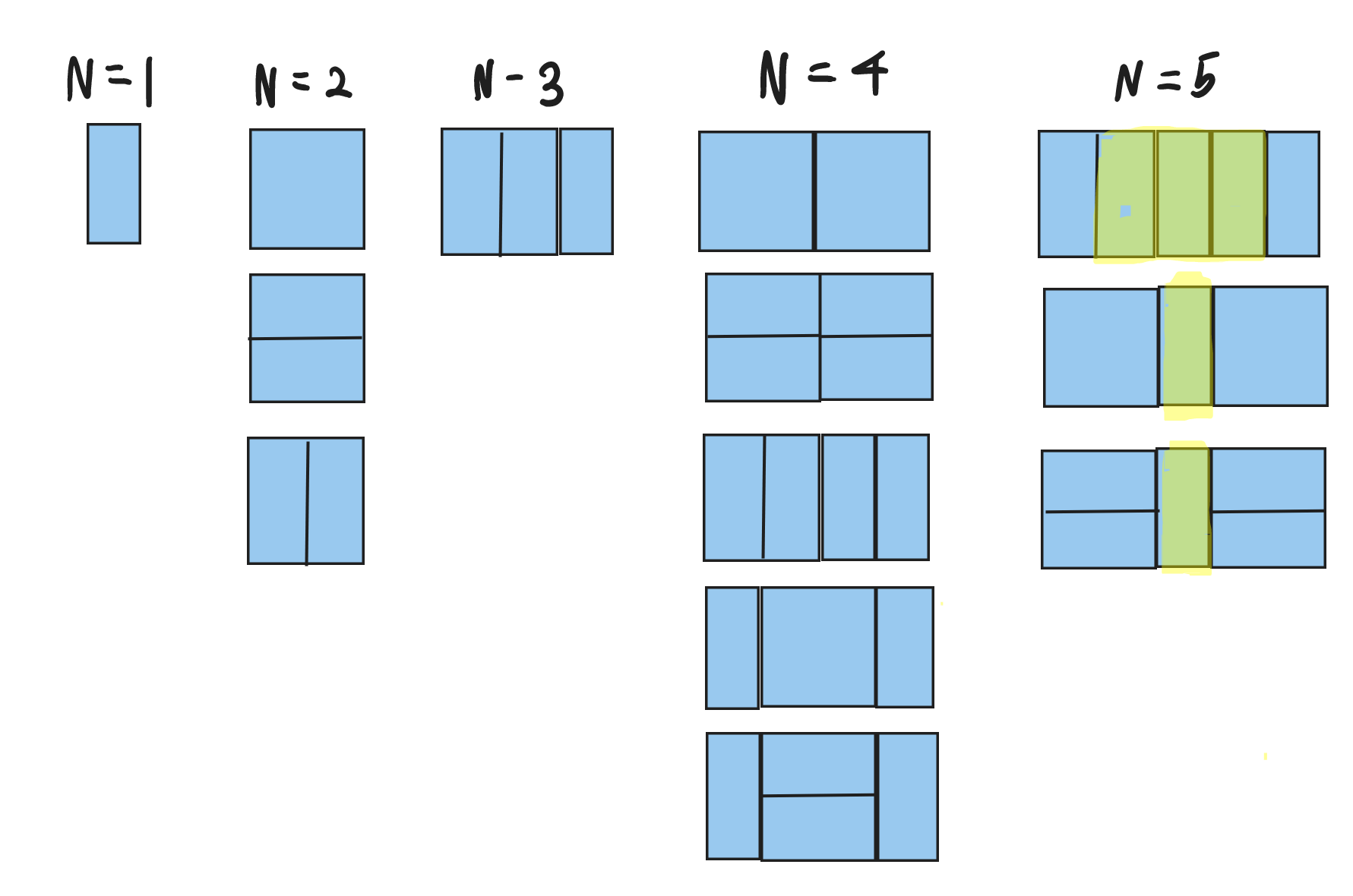
N=5부터 비로소 형태가 보이기 시작한다.
노란 부분의 타일 구성을 보면
N=3일때의 구성과, N=1일때의 구성의 양쪽에 타일을 덧대서 완전 대칭을 만들어낸 것이다.
결국 점화식은
(길이 N인 완전 대칭 타일 구성) = (길이 N-2의 타일 구성의 양쪽에 2x1 타일을 덧댄 구성) + (길이 N-4의 타일 구성의 양쪽에 2*2 혹은 1*2(2개)를 덧댄 구성)이라고 할 수 있고, 이를 식으로 나타내면
dp[N] = dp[N-2] + dp[N-4] * 2이다.
이제 완전 대칭 타일 갯수를 구하는 방법까지 알았으므로, 코드를 완성해보자.
fun solution() = with(System.`in`.bufferedReader()) {
val N = readLine().toInt()
val dp = IntArray(N + 1)
// 아래에서 인덱스 5까지 접근할 예정이라 early return
if (N in 1..4) {
when (N) {
1 -> print(1)
2, 3 -> print(3)
4 -> print(8)
}
return
}
// 전체 타일 구성 개수 계산
dp[1] = 1; dp[2] = 3;
for (n in 3..N) {
dp[n] = dp[n - 1] + dp[n - 2] * 2
}
// 완전 대칭 타일 구성 개수 계산
val dpSym = IntArray(N + 1)
dpSym[1] = 1; dpSym[2] = 3;
dpSym[3] = 1; dpSym[4] = 5;
for (n in 5..N) {
// N보다 길이 2만큼 짧은 곳 양쪽에 2*1 블럭 붙이기 or 길이 4만큼 짧은 곳 양쪽에 2*2 or 1*2 블록 붙이기
dpSym[n] = dpSym[n - 2] + dpSym[n - 4] * 2
}
// 전체 - 완전 대칭 경우의 수 제외하고, 중복되는 구성을 반으로 나누기 (2개씩 존재하는 대칭의 개수)
print(dp[N] - (dp[N] - dpSym[N]) / 2)
}다 풀고나서 보니 골드4라기엔 어려운 문제였던 것 같다.
